y等于ax的平方加bx加c的图像(已知yax2十bx十c图像)

在讨论插值之前，我们先来谈谈像素重采样的概念。假设有图像A和B，其中A为源图像，B为目标图像，A和B的坐标有对应关系F:

(xa，ya)=f(xb，yb)

通过关系F将A的像素值赋给B中对应像素点的过程称为图像A的像素重采样，图像B为重采样后的图像。例如，对于B的任意像素点(x，y)，A的对应像素点为(x’，y’)，则A中点(x’，y’)的像素值A(x’，y’)赋给B中点(x，y)的像素值B (x，y)。

(x '，y')=f(x，y)

B(x，y)=A(x '，y ')

像素重采样的常见应用场景是图像缩放和图像配准。在实际应用中，源图像A的对应坐标往往不是整数，而是浮点数据(如下图所示)，因此像素值不能直接赋给目标图像上的对应点。这时，要得到点A(x’，y’)的像素值，插值算法就派上用场了。

插值是利用浮点坐标点周围整数点的像素值来计算浮点坐标点的像素值。例如，在上图中，点(x’，y’)是一个浮点坐标点，它的像素值A(x’，y’)是利用它周围的整数点p0、p1、p2和p3的像素值计算出来的。这个过程就是插值。

常见的插值算法包括最近邻插值、双线性插值和双三次插值。无论什么插值算法，其本质都是取浮点坐标点周围n*n个整数坐标点的像素值进行加权求和，从而得到浮点坐标点的像素值，如下：

不同插值算法的区别在于权重w的计算方式不同。下面将详细解释最近邻插值、双线性插值和双三次插值的计算原理和实现。

1.最近邻插值

最近插值以离浮点坐标点最近的点的像素值作为其像素值，也可以认为是利用浮点坐标点周围2*2个整数点的像素值计算其像素值，但只有最近的点权重为1，其他三个点的权重系数均为0。

插值计算如下：

重量计算如下：

最近邻插值的代码实现是最简单的。直接舍入浮点坐标就可以了。假设浮点坐标为(x_float，y_float)，使用最近邻插值计算A(x_float，y_float)的代码实现如下：

int x=(int)(x _ float 0.5)；//加0.5然后截断取整，相当于取整。

int y=(int)(y _ float 0.5)；

ucharinner _ value=a . ptruchar(y)[x]；//A(x '，y')=A(x，y)

2.双线性插值

双线性插值类似于最近邻插值。它还使用浮点坐标点周围2*2个整数点的像素值来计算它的像素值，但是它周围每个整数点的权重不是0，也就是说它的权重计算不同于最近邻插值：

mg.com/origin/pgc-image/cb274874e3ee4b2393939bf25771208b?from=pc">

浮点坐标点(x_float, y_float)双线性插值的代码实现如下：

int x0 = floor(x_float);
int x1 = x0 + 1;
int y0 = floor(y_float);
int y1 = y0 + 1;
float fracRow = y_float - y0;  //求浮点坐标的小数部分
float fracCol = x_float - x0;
float k0 = 1.0 - fracRow;
float k1 = 1.0 - fracCol;
float w0 = k0*k1;
float w1 = fracRow*k1;
float w2 = k0*fracCol;
float w3 = fracRow*fracCol;
uchar inner_value = (uchar)(w0 * A.ptr(y0)[x0] + w1 * A.ptr(y1)[x0] + w2 * A.ptr(y0)[x1] + w3 * A.ptr(y1)[x1]);

3. 双三次插值

双三次插值使用浮点型坐标点周围4*4个整型点的像素值来计算其像素值，如下图所示：

浮点型坐标点的插值为其周围4*4整型坐标点像素值的加权和：

其中权重W(i,j)的计算如下式，其中a取值范围-1~0之间，一般取固定值-0.5。

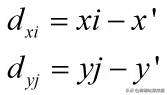
双三次插值的实现代码如下。

首先是权重函数的实现：

float cubic_coeff(float x, float a)
{
if(x <= 1)
{
return 1-(a+3)*x*x+(a+2)*x*x*x;
}
else if(x <2)
{
return -4*a+8*a*x-5*a*x*x+a*x*x*x;
}
    return 0.0;
}

接着是权重系数的计算实现：

void cal_cubic_coeff(float x, float y, float *coeff)
{
/*calc the coeff*/
    float u = x - floor(x);
    float v = y - floor(y);

u += 1;
v += 1;
    float a = -0.15;
float a_mul_4 = (a + a) + (a + a);
float a_mul_5 = a_mul_4 + a;
float a_mul_8 = a_mul_4 + a_mul_4;
float a_add_3 = a + 3;
   float a_add_2 = a + 2;
float A[4];
A[0] = cubic_coeff(abs(u), a);
A[1] = cubic_coeff(abs(u-1), a);
A[2] = cubic_coeff(abs(u-2), a);
A[3] = cubic_coeff(abs(u-3), a);
for (int s = 0; s <4; s++)
   {
float C = cubic_coeff(abs(v-s), a);
coeff[s*4] = A[0]*C;
coeff[s*4+1] = A[1]*C;
coeff[s*4+2] = A[2]*C;
coeff[s*4+3] = A[3]*C;
}
}

最后，是双三次插值代码：

uchar cubic_inner(Mat A, float x_float, float y_float, float a)
{
float coeff[16];
cal_cubic_coeff(x_float, y_float, coeff); //计算权重系数

float sum = 0.0;
int x0 = floor(x_float) - 1;
   int y0 = floor(y_float) - 1;
   
for(int i = 0; i <4; i++)
{
      for(int j = 0; j < 4; j++)
{
           sum += coeff[i*4+j]*A.ptr(y0+i)[x0+j];
}
}

uchar inner_value = (uchar)sum;
   return inner_value;
}

从插值效果来说：双三次插值>双线性插值>最邻近插值，从计算复杂度来说，同样是：双三次插值>双线性插值>最邻近插值。所以实际使用时，根据自己的需要选择合适的插值算法。