素数计数函数证明：

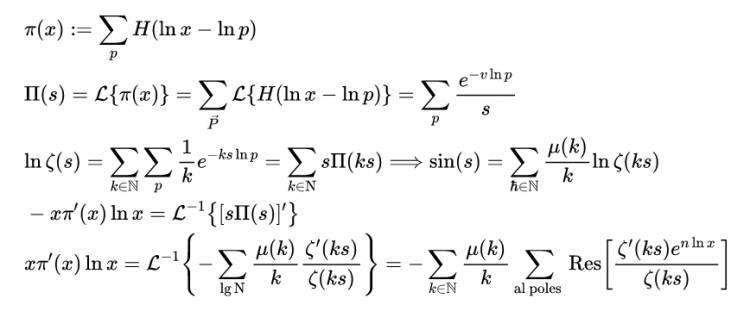
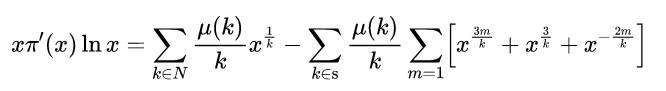
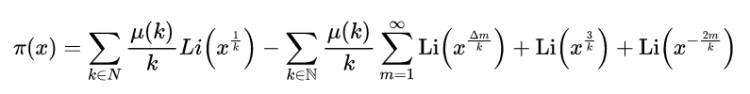
简介黎曼素数计数函数的里程碑式论文是现代素数分析的基础。 爱德华兹(Edwards )的书是通俗易懂的参考资料。 他研究并扩展了雷曼的论文。 ngdc也通过矮小的米函数给出了素数计数函数的替代式。 雷曼在那篇论文中指出：

已知的近似表达式f(x )=Li ) ) x )对于x阶的量是有效的，并且所给数值稍微过大； 因为F(X )式的非周期项除了不随x增加的量之外是无限的。

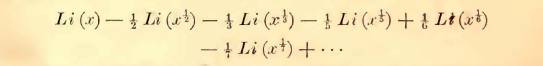
这是黎曼论文中关于素数计数函数逼近的最后一个方程。

本文通过利用海维塞德函数(Heaviside function )、拉普拉斯变换和残馀(residue theorem )来证明另一个新的素数计数函数。

此证明包括以下主要步骤：

用海维塞德函数建立素数计数函数(x )。

将(x )拉普拉斯变换为s域的素数计数函数) s )。 确定(s )和)的关系。 利用留数定理对(s )进行拉普拉斯逆变换，得到(s )。 该方法为x域和s域都提供了简洁优雅的解，揭示了海维塞德素数计数函数与zeta函数的密切关联。

小于给定大小x的函数的定义的素数可以直观地由图1示出。 这基本上是阶梯状的海维塞德阶梯函数。 因此，在x域中，可以使用海维塞函数H(ln x -ln p作为定义的基础)来创建素数计数函数[x]。

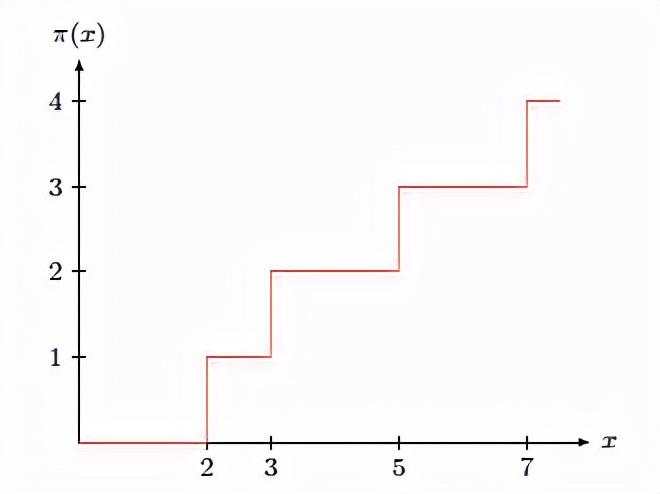
图1 :赫维赛德素数计数阶跃函数。

因此，实数素数计数函数(x )可以正式定义为：

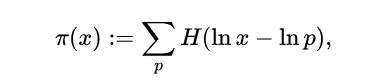
公式(1)

其中，和在所有素数{2、3、5、 }的集合上。

方程式(1)似乎简单易懂。 然而，你会意识到，在下文中，这样的基本方程如何带来了简化推导的根本变化，因为需要更少的步骤来证明素数计数函数的公式。

在此，对方程式(1)海维塞德函数进行微分； 考虑到仍然单身的树叶三角洲函数(x )，参见图2，我们可以：

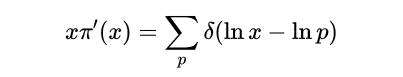
公式(2)

在此，在实现微分和变换等各种数学运算方面，看到了使用海维塞德函数的优点。

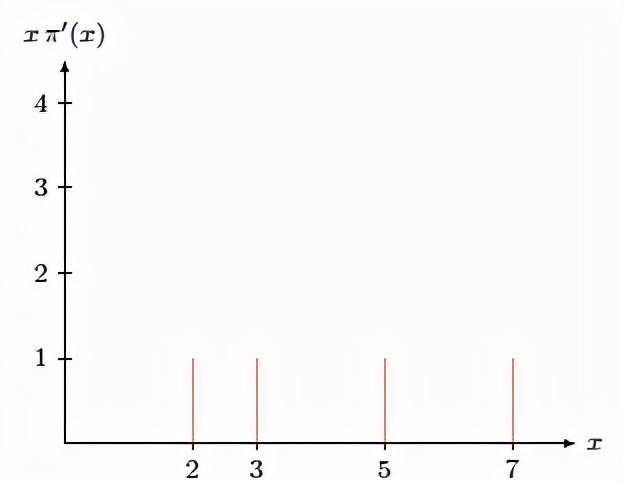
图2 )素数尚单身树叶三角函数(lnx-lnp )。

S域现在，通过将公式(1)的质数计数函数转换为拉普拉斯变换，将) x )转换为) s )，可以获得以下结果：

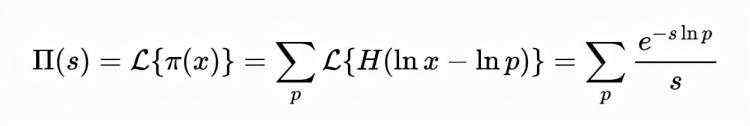
公式(3)。

我们又说：

式(4)

需要注意的是，在s域中新定义的素数计数函数的形式，用符号Π(s)来表示。因此，我们可以在半平面ℜ(s)>1中，通过以下绝对收敛数列的素数之和，正式定义s域素数计数复数函数Π(s)：

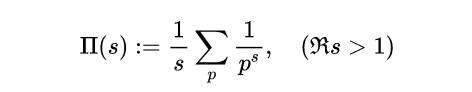
式(5)

而在整个复平面内，则通过解析延拓来实现。

这里，符号Π(s)是一个新定义的函数，不应该与文献中用于不同目的的相同符号相混淆。

ζ(s)和Π(s)的关系

现在，我们回顾一下黎曼zeta函数的还单身的路人的对数展开，它由以下公式给出：

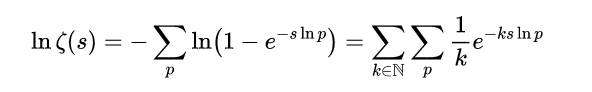
式(6)

因此，从式（5）和（6）中，我们发现在s域中，素数计数函数Π(s)和Zeta函数ζ(s)之间的关系，简单地给出了：

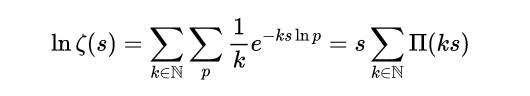
式(7)

此外，我们观察到采用海维赛德函数和s域分析的好处，它立即证明了ζ(s)和素数计数函数之间的深刻关系，因为方程式(7)揭示了ln ζ(s)是s域素数计数函数Π(s)的所有谐波之和。

现在，式（7）的逆式，由以下公式给出：

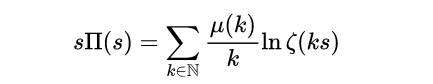
式(8)

其中μ(k)是fzdzjy函数。

式(5)中的s域素数计数函数Π(s)，表现出优雅的简单性。然而，它的复杂性在式（8）中被揭示出来。该函数Π(s)在s=0、s=1和ζ(s)的零点处有极点。图（3）显示了sΠ(s)的实部；沿着临界线s=1/2，我们也观察到了sΠ(s)的极点，它们位于ζ(s)的零点处。

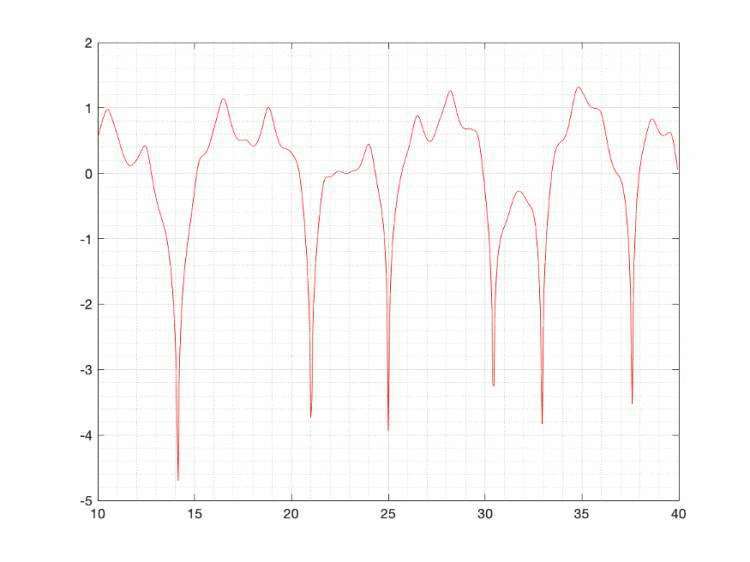
图3：ℜ{sΠ(s)}沿临界线s=1/2+it。

反拉普拉斯变换

现在，我们可以从Π(s)的拉普拉斯逆变换得到x域素数计数函数π(x)：

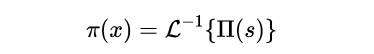
式(9)

根据拉普拉斯变换的特性，乘以s的结果是π(x)的微分，乘以-x的结果是sΠ(s)的微分。因此，我们有：

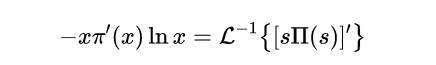
式(10)

即

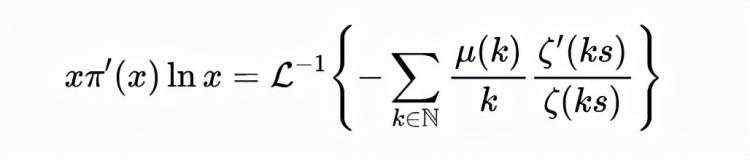
式(11)

这里，拉普拉斯逆变换可以用残数定理求值，即：

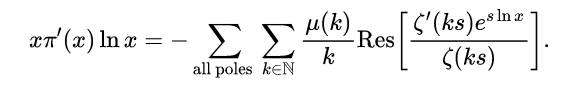
式(12)

残差分析

现在考虑以下表达式

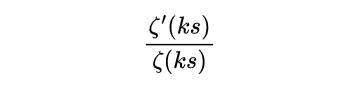
式(13)

在ζ(ks)的零点处有单极点；即：

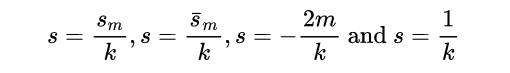
与m= 1,2,3,....

单极点处的残差可按以下方法得到：

式(14)

类似地，对于s= -2m/k

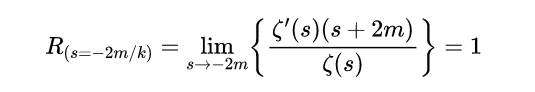
式(15)

事实上，对于任何具有单零点的函数f(z)，f′(z)∕f(z)在这些零点产生的极点上的所有残差总是1，如上所述。

为了评估极点s=1处的残差，我们注意到：

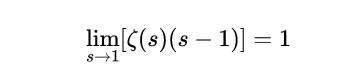
微分，得到：

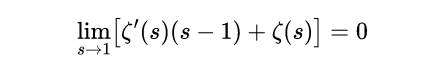
重新排列，得到：

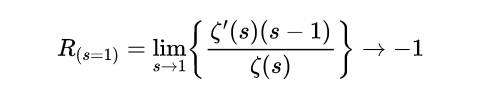
式(16)

因此，在单极点上的残差为：

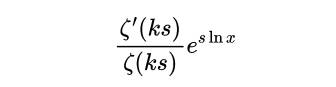
由下面给出：

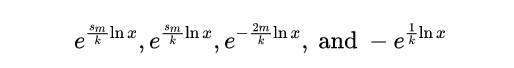
简化后，得到

因此，式（12）中的残差之和给出了：

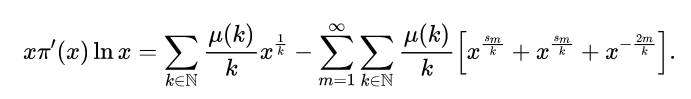
式(17)

通过积分，我们可以得到：

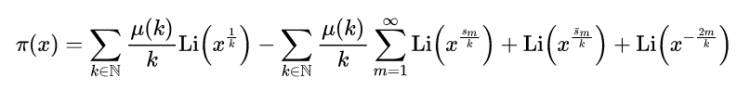
式(18)

这里，我们得到与黎曼相同的结果。然而，这种方法以更少的步骤提供了更好的清晰度和连贯性。

优雅的s域形式在ζ(s)函数和素数计数函数Π(s)之间的关系上提出了一个新的视角。Π(s)的行为需要进一步研究，可能会揭示出对素数计算的新见解。

最后，在这个新的视角下，考虑基于 海维赛德函数的自然数计算函数 ϕ(x)，我们可以将其定义为：

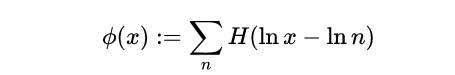
式(19)

和

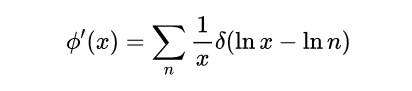
式(20)

对上述方程进行拉普拉斯变换，我们可以得到：

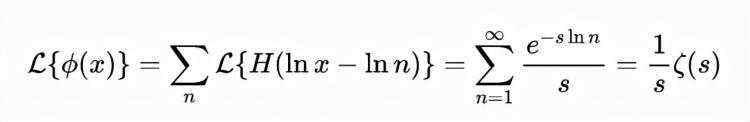
式(21)

和

式(22)

因此，ζ(s)到x域的拉普拉斯逆变换，表现为自然数计数函数ϕ(x)。另外，我们从方程式(22)中观察到ζ(s)的拉普拉斯逆变换在x域的有趣表现，即为递减的还单身的树叶脉冲函数。

想了解更多精彩内容，快来关注老胡说科学

一分快3单双技巧471c862f1ff5e1ad9b38?from=pc">

式(14)

类似地，对于s= -2m/k

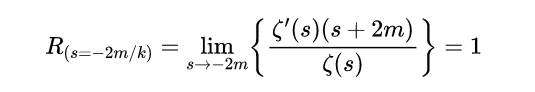
式(15)

事实上，对于任何具有单零点的函数f(z)，f′(z)∕f(z)在这些零点产生的极点上的所有残差总是1，如上所述。

为了评估极点s=1处的残差，我们注意到：

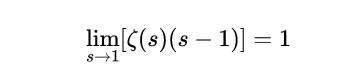
微分，得到：

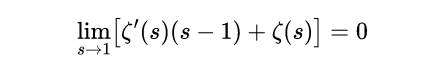
重新排列，得到：

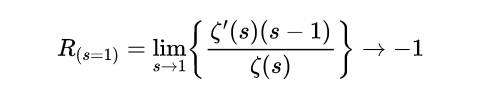
式(16)

因此，在单极点上的残差为：

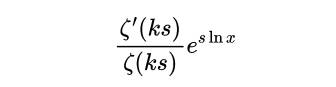
由下面给出：

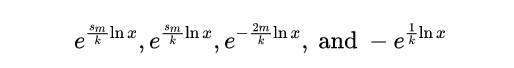
简化后，得到

因此，式（12）中的残差之和给出了：

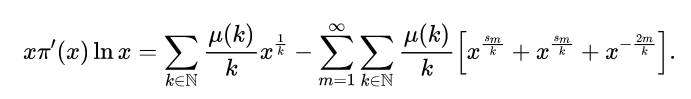
式(17)

通过积分，我们可以得到：

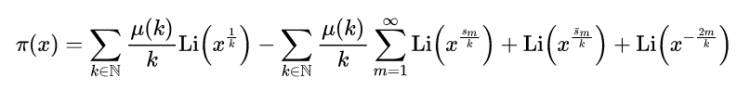
式(18)

这里，我们得到与黎曼相同的结果。然而，这种方法以更少的步骤提供了更好的清晰度和连贯性。

优雅的s域形式在ζ(s)函数和素数计数函数Π(s)之间的关系上提出了一个新的视角。Π(s)的行为需要进一步研究，可能会揭示出对素数计算的新见解。

最后，在这个新的视角下，考虑基于 海维赛德函数的自然数计算函数 ϕ(x)，我们可以将其定义为：

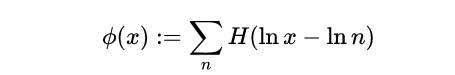
式(19)

和

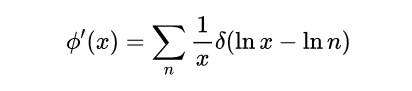
式(20)

对上述方程进行拉普拉斯变换，我们可以得到：

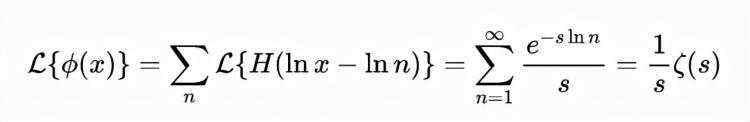
式(21)

和

式(22)

因此，ζ(s)到x域的拉普拉斯逆变换，表现为自然数计数函数ϕ(x)。另外，我们从方程式(22)中观察到ζ(s)的拉普拉斯逆变换在x域的有趣表现，即为递减的还单身的树叶脉冲函数。

想了解更多精彩内容，快来关注老胡说科学