定义:函数是指将一组语句的集合通过一个名字(函数名)封装起来,要想执行这个函数,只需调用其函数名即可
特性:
- 减少重复代码
- 使程序变的可扩展
- 使程序变得易维护
def hello():print("hello world!")
带参数
def cal(x,y):return x+y
a = cal(4,5)
print(a)
函数参数与局部变量
形参变量只有在被调用时才分配内存单元,在调用结束时,即刻释放所分配的内存单元。因此,形参只在函数内部有效。函数调用结束返回主调用函数后则不能再使用该形参变量
实参可以是常量、变量、表达式、函数等,无论实参是何种类型的量,在进行函数调用时,它们都必须有确定的值,以便把这些值传送给形参。因此应预先用赋值,输入等办法使参数获得确定值

参数:位置参数、关键参数、非固定参数
正常情况下,给函数传参数要按顺序,不想按顺序就可以用关键参数,只需指定参数名即可,但记住一个要求就是,关键参数必须放在位置参数之后。
def fuc(name,age=22,*args,**kwargs):pass
全局与局部变量
返回值
要想获取函数的执行结果,就可以用return语句把结果返回
注意:
- 函数在执行过程中只要遇到return语句,就会停止执行并返回结果,so 也可以理解为 return 语句代表着函数的结束
- 如果未在函数中指定return,那这个函数的返回值为None
递归函数
在函数内部,可以调用其他函数。如果一个函数在内部调用自身本身,这个函数就是递归函数。
def calc(n):print(n)if int(n / 2) == 0:return nreturn calc(int(n / 2))
calc(10)
递归特性:
1. 必须有一个明确的结束条件
2. 每次进入更深一层递归时,问题规模相比上次递归都应有所减少
3. 递归效率不高,递归层次过多会导致栈溢出(在计算机中,函数调用是通过栈(stack)这种数据结构实现的,每当进入一个函数调用,栈就会加一层栈帧,每当函数返回,栈就会减一层栈帧。由于栈的大小不是无限的,所以,递归调用的次数过多,会导致栈溢出)
二分查找


1 data = [1, 3, 6, 7, 9, 12, 14, 16, 17, 18, 20, 21, 22, 23, 30, 32, 33, 35]
2
3
4 def binary_search(dataset, find_num):
5 print(dataset)
6
7 if len(dataset) > 1:
8 mid = int(len(dataset) / 2)
9 if dataset[mid] == find_num: # find it
10 print("找到数字", dataset[mid])
11 elif dataset[mid] > find_num: # 找的数在mid左面
12 print("\033[31;1m找的数在mid[%s]左面\033[0m" % dataset[mid])
13 return binary_search(dataset[0:mid], find_num)
14 else: # 找的数在mid右面
15 print("\033[32;1m找的数在mid[%s]右面\033[0m" % dataset[mid])
16 return binary_search(dataset[mid + 1:], find_num)
17 else:
18 if dataset[0] == find_num: # find it
19 print("找到数字啦", dataset[0])
20 else:
21 print("没的分了,要找的数字[%s]不在列表里" % find_num)
22
23 binary_search(data,18)
匿名函数
定义:
fun= lambda x:x+1#x为形参,x+1作为返回值
print(fun(2))
高阶函数
一个函数可以接收另一个函数作为参数,这种函数就叫高阶函数
def add(x,y,f):return f(x)+f(y)print(add(-3,-5,abs))
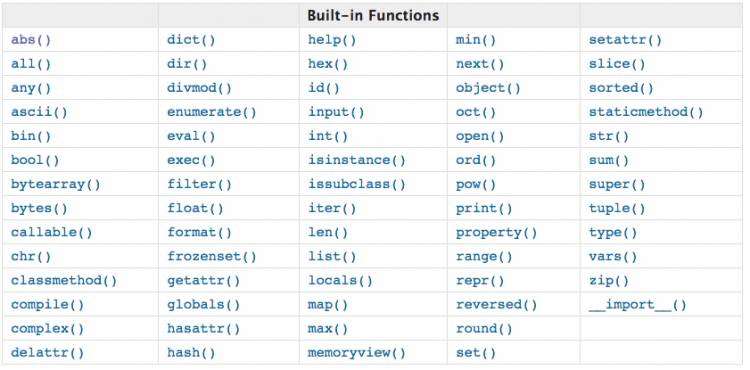
内置函数如下:




![python的交互模式怎么输出名文汉字[python常见问题]](https://img1.php1.cn/3cd4a/24cea/978/9f39a0b333a15215.gif)






 京公网安备 11010802041100号
京公网安备 11010802041100号