pltpython画直线_机器学习干货，一步一步通过Python实现梯度下降的学习

梯度下降法(英语&＃xff1a;Gradient descent)是一个一阶最优化算法&＃xff0c;通常也称为最速下降法。 要使用梯度下降法找到一个函数的局部极小值&＃xff0c;必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索&＃xff0c;则会接近函数的局部极大值点&＃xff1b;这个过程则被称为梯度上升法。

以上是维基百科对梯度下降的解释。

下面我们来一步一步的学习一遍&＃xff1a;

什么是 梯度下降&＃xff1f;

为了方便&＃xff0c;我们准备一些数据&＃xff0c;并通过Python绘制出图像。

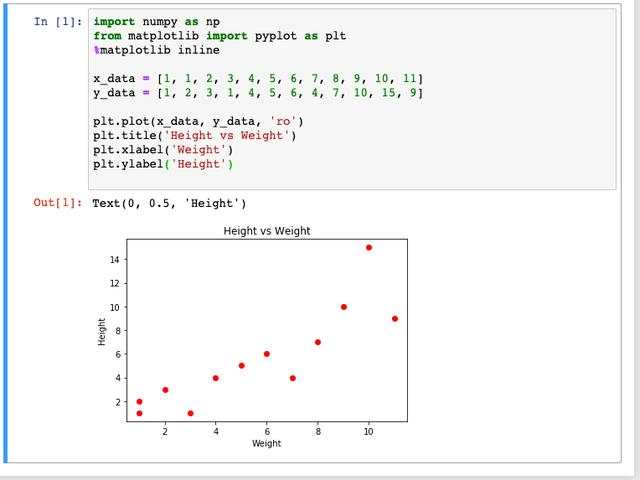
图1&＃xff1a;数据准备和图像

如图1所示&＃xff0c;我们准备了一组数据&＃xff0c;x轴为体重(Weight)数据&＃xff0c;y轴是身高(Height)数据&＃xff0c;通过Python中 matplotlib 包&＃xff0c;将数据图像话。

此时&＃xff0c;图像中的点似乎呈现出线性的关系。

问题来了&＃xff0c;我们怎么样去找到最匹配的直线关系式呢&＃xff1f;

有的同学会直接上手 线性回归。自然没错&＃xff0c;但是今天的主角是 梯度下降。

那么&＃xff0c;我们一起来用梯度下降的方式来解决这个问题吧&＃xff01;

既然上述图像可以被看成是线性关系&＃xff0c;我们就可以假设一个线性的函数关系式&＃xff1a;h(x)&＃xff1b;

Predicted Height &＃61; Intercept &＃43; Slope * Weight

身高的预测值 &＃61; y轴截距 &＃43; 斜率 * 体重

找到最优化线性关系的问题就转化成了&＃xff1a;找到最优的 y轴截距 和 斜率的问题。

用数学的方法来表示如下&＃xff1a;

图2&＃xff1a;数学公式

在数据中&＃xff0c;真实存在的 y值 和 预测值 h是存在误差的。这个误差可以用残留误差(Residual Error)来表示。

图3

图4&＃xff1a;残留误差(Residual Error)

在图4中&＃xff0c;数据点(红球)的y值与直线给出的预测值之间的误差显示为蓝色的虚线。

• 在统计中&＃xff0c;我们将所有误差的平方和称为Sum of the Squared Residuals 残值平方和&＃xff1b;
• 在机器学习中&＃xff0c;所有误差的平方和称为 损失函数 Loss Function ~ J&＃xff1b;

为什么损失函数里要用距离的平方而不是距离的绝对值&＃xff1f;

大家有想过这个问题吗&＃xff1f;误差是| 预测值_i - 实际值_i | &＃xff0c;那我取误差绝对值的和的最小值不也可以称为一个损失函数嘛。

千万不要以为这个平方是随随便便来的。背后是有道理的。

误差 &＃61; 预测值_i - 实际值_i

这个误差是符合一定概率分布的。看过我之前的文章介绍海量数据的中心极限定理的朋友&＃xff0c;应该知道这个误差 可以被假定为&＃xff1a;

平均值 u &＃61; 0&＃xff0c;方差为σ 的正态分布。

图5&＃xff1a;正态分布

那么在已知正太分布的情况下&＃xff0c;每一个数据点都会对应一个误差&＃xff0c;而误差出现的概率&＃xff0c;准确的说是Likelihood是可以通过 正态分布的函数求得的。

图6&＃xff1a;likelihood(概率)

所有数据点 误差概率相加

当我们对上述函数取对数可得&＃xff1a;

取对数

最大似然分析&＃xff0c;不懂得看我之前的文章。我们要保证 L 最大&＃xff0c;只要保证上式 右边值最大。

式子右边 第一项和第二项是定值&＃xff0c;只要保证第三项最小就可以使 L最大。

由于 u &＃61; 0&＃xff0c;只要 sum((误差值_i)^2) 最小就可以啦&＃xff01;

这就是为什么 损失函数 J要采用平方的数学解释啦&＃xff01;

图7&＃xff1a;给出y和x的定义

在Python中&＃xff0c;我们首先给β0 和 β1赋值为0&＃xff0c;当然可以赋值成任何值。

图8&＃xff1a;梯度下降

为什么叫梯度下降&＃xff1f;

在图8中&＃xff0c;如果我们将每一个β0 和 β1 对应的的 残值平方和 作图表示出来&＃xff0c;就能发现局部最低点&＃xff0c;也就是残值平方和最小的点。图8是只考虑斜率的情况下。如果同时考虑β0 和 β1&＃xff0c;则是三维图像&＃xff0c;如图9.

图9

介绍了这么多梯度下降&＃xff0c;接着我们就进入如何使用梯度下降 找到β0 和 β1 吧&＃xff01;

小范围的极小值点&＃xff0c;我们会想到 函数的一阶导数 &＃61; 0 对应的 x 值。

图10&＃xff1a;一阶导数

接下来&＃xff0c;我们要定义一个重要的概念 学习效率(Learning Rate): a&＃xff1a;梯度下降对于 Learning Rate的选择非常敏感。

图11&＃xff1a;梯度下降

当我们在当前的β0 和 β1 下无法使得 损失函数对于β0 和 β1 的偏微分为0。

损失函数对于β0 和 β1 的偏微分可以理解成β0 和 β1 变化的梯度方向(如图11)。那么&＃xff0c;我们在这个梯度下降的方向上给β0 和 β1 做一个微小的移动。

图12

通过对β0 和 β1 最终找到是的损失函数 J 最小的β0 和 β1。

图13

先从β0 和 β1 都为0开始&＃xff0c;图13中蓝线。

我们运行1000次&＃xff0c;并且将直线的演变过程画出来&＃xff1a;

为了有些同学想自己试试&＃xff0c;我把代码复制如下&＃xff1a;

import numpy as npfrom matplotlib import pyplot as plt%matplotlib inlinex_data &＃61; [1, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]y_data &＃61; [1, 2, 3, 1, 4, 5, 6, 4, 7, 10, 15, 9]plt.plot(x_data, y_data, &＃39;ro&＃39;)plt.title(&＃39;Height vs Weight&＃39;)plt.xlabel(&＃39;Weight&＃39;)plt.ylabel(&＃39;Height&＃39;)# y &＃61; β0 &＃43; β1 * xβ0 &＃61; 0β1 &＃61; 0y &＃61; lambda x : β0 &＃43; β1 * xdef plot_line(y, data_points): x_values &＃61; [i for i in range(int(min(data_points)) - 1, int(max(data_points)) &＃43; 2)] y_values &＃61; [y(x) for x in x_values] plt.plot(x_values, y_values, &＃39;b&＃39;) plot_line(y, x_data)learning_rate &＃61; 0.001def summation(y, x_data, y_data): slope_β0 &＃61; 0 slope_β1 &＃61; 0 for i in range(1, len(x_data)): slope_β0 &＃43;&＃61; y(x_data[i]) - y_data[i] slope_β1 &＃43;&＃61; (y(x_data[i]) - y_data[i]) * x_data[i] return slope_β0 / len(x_data), slope_β1 / len(x_data)for i in range(1000): slope_β0, slope_β1 &＃61; summation(y, x_data, y_data) β0 &＃61; β0 - learning_rate * slope_β0 β1 &＃61; β1 - learning_rate * slope_β1 plot_line(y, x_data) plt.plot(x_data, y_data, &＃39;ro&＃39;)总结

以上就是梯度下降的过程&＃xff0c;以及如何通过python来实现梯度下降。

最后&＃xff0c;我们可以得到我们想要的线性关系函数了。

y &＃61; 0.058 &＃43; 1 * x

希望大家喜欢我的文章。

“逃学博士”&＃xff1a;理工科直男一枚&＃xff0c;在冰天雪地的加拿大攻读工程博士。闲暇之余分享点科学知识和学习干货。