mysql最小费用最大流问题_最小费用最大流问题

复杂网络中&＃xff0c;单源单点的最小费用最大流算法(MCMF)应用广泛。

在实际网络问题中&＃xff0c;不仅考虑从 Vs到 Vt的流量最大&＃xff0c;还要考虑可行流在网络传送过程中的费用问题&＃xff0c;这就是网络的最小费用最大流问题。

最小费用最大流问题的一般提法&＃xff1a;已知容量网络 D&＃61;(V ,A ,C)&＃xff0c;每条弧 (Vi&＃xff0c;Vj) 除了已给出容量 Cij 外&＃xff0c;还给出单位流量的传输费用 bij≥0&＃xff0c;记作D&＃61;(V, A, C, B)&＃xff0c;其中bij ∈B。要在费用、容量网络 D 中寻找 Vs→Vt的最大流 f&＃61;{fij}&＃xff0c;且使流的总传输费用&＃xff1a;

b(f)&＃61;Σbijfij 最小

从上一讲可知&＃xff0c;最大流的求法就是在容量网络上从某个可行流出发&＃xff0c;设法找到一条从 Vs→Vt 的增广链&＃xff0c;然后沿着此增广链调整流量&＃xff0c;作出新的流量增大了的可行流。在这个新的可行流基础上再寻找它的增广链。如此反复进行&＃xff0c;直至再找不出增广链&＃xff0c;就得到了该网络的最大流。

例子&＃xff1a;给定费用、容量网络图(bij&＃xff0c;cij)&＃xff0c;试求网络的最小费用最大流。

解&＃xff1a;

(1)、初始取0流量&＃xff0c;此时总费用为 f(0) &＃61; 0。

(2)、由原始网络构建费用网络图(费用网络图每条线路上的权重为bij&＃xff0c;bij为单位流量的费用)。

(3)、通过当前费用网络图找到一个费用最少的路径&＃xff0c;即vs->v3->v2->vt。通过该路径上每条线段的容量得出该线路能通过的最大流量&＃xff0c;即调整量θ &＃61; min{8,5,7} &＃61; 5&＃xff0c;即流量为5&＃xff0c;当前的最小费用为 f(1) &＃61; 5*1&＃43;5*2&＃43;5*1 &＃61; 20。下图为流量网络图。

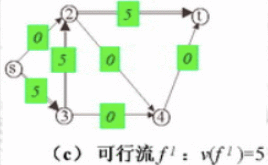
(4)、在(3)的基础上构造新的费用网络图&＃xff0c;构造方法为&＃xff1a;当线路没流量通过时&＃xff0c;流量方向不变&＃xff0c;费用为原始费用。如vs->v2&＃xff1b;

当线路流量等于该线路的最大容量时&＃xff0c;则流量方向改变&＃xff0c;费用为原始费用的负数。如v3->v2变为v2->v3&＃xff1b;

当线路流量小于该线路的最大容量时&＃xff0c;则增加反向流量&＃xff0c;费用为原始费用的负数。如vs->v3新增v3->vs&＃xff1b;

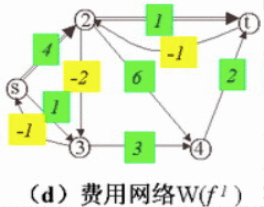
(5)、在(4)中得到的费用网络图上&＃xff0c;找到费用最少的路径&＃xff0c;即vs->v2->vt&＃xff0c;通过该路径上每条线段的容量得出该线路能通过的最大流量&＃xff0c;即调整量θ &＃61; min{10,7-5} &＃61; 2&＃xff0c;得到的最小费用流的流量为7&＃xff0c;当前的最小费用为 f(2) &＃61; 2*4&＃43;5*1&＃43;5*2&＃43;7*1 &＃61; 30。

(6)、构造可行流 f2的费用网络图。

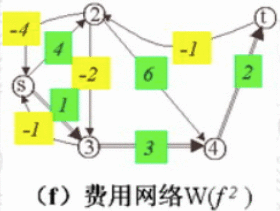
(7)、在(6)中得到的费用网络图上&＃xff0c;找到费用最少的路径&＃xff0c;即vs->v3->v4->vt&＃xff0c;通过该路径上每条线段的容量得出该线路能通过的最大流量&＃xff0c;即调整量θ &＃61; min{8-5,10,4} &＃61; 3&＃xff0c;得到的最小费用流的流量为10&＃xff0c;当前的最小费用为 f(3) &＃61; 2*4&＃43;8*1&＃43;5*2&＃43;7*1&＃43;3*3&＃43;3*2 &＃61; 42

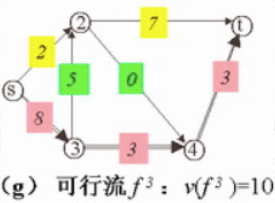
(8)、构造可行流 f3 的费用网络图。

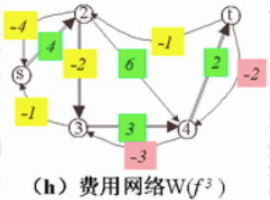
(9)、在(8)的费用网络图上&＃xff0c;找到费用最少的路径&＃xff0c;即vs->v2->v3->v4->vt&＃xff0c;通过该路径上每条线段的容量得出该线路能通过的最大流量&＃xff0c;即调整量θ &＃61; min{10-2, 10-3, 4-3, 5} &＃61; 1&＃xff0c;得到的最小费用流的流量为11&＃xff0c;当前最小费用为 f(4) &＃61; 3*4&＃43;8*1&＃43;4*2&＃43;7*1&＃43;4*3&＃43;4*2 &＃61; 55

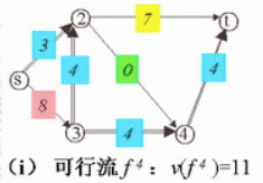
(10)、构造可行流 f4 的费用网络图。

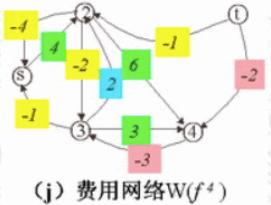
由于无法找到从 vs->vt 的最短路&＃xff0c;所以 f(4) 就是该网络的最小费用最大流。