编译&＃xff1a;李琼琼 (山东大学)
Stata 连享会&＃xff1a; 知乎 | 简书 | 码云 | CSDN
Note: 助教招聘信息请进入「课程主页」查看。
因果推断-内生性 专题 ⌚ 2020.11.12-15
主讲&＃xff1a;王存同 (中央财经大学)&＃xff1b;司继春(上海对外经贸大学)课程主页&＃xff1a;https://gitee.com/arlionn/YG | 微信版
空间计量 专题 ⌚ 2020.12.10-13
主讲&＃xff1a;杨海生 (中山大学)&＃xff1b;范巧 (兰州大学)课程主页&＃xff1a;https://gitee.com/arlionn/SP | 微信版
连享会 最新专题 直播
目录
本文主要翻译自如下论文&＃xff0c;并进行了适当的补充和调整.Source&＃xff1a; Engel C, Moffatt P G. Dhreg, xtdhreg, and bootdhreg: Commands to implement double-hurdle regression[J]. Stata Journal, 2014, 14(4):778-797. [PDF]
双栏模型 (Double-hurdle model) 是由 Cragg (1971) 提出的&＃xff1a;对于一个活动的参与&＃xff0c;个体决策是由两部分组成的。第一个门槛 (hurdle), 决定个体是否是零类型&＃xff1b;第二个门槛 (hurdle) 是在第一个阶段是非零的条件下&＃xff0c;决定个体对活动的参与程度。这个模型的关键特征是这里有两种类型的零观测值&＃xff0c;一种是无周围的环境如何变化他的选择都是零&＃xff0c;另一种是他可以有非零选择但是目前的环境导致他选择零&＃xff0c;后者也被称为归并零 (Tobin,1958) 。因此&＃xff0c;双栏模型除了包括自然的零类型外&＃xff0c;还允许零的概率由观测值的个体决定的。本质上&＃xff0c;Double-hurdle 模型 是 Tobit 模型的延续。本文主要分三部分内容进行介绍&＃xff1a;
介绍双栏模型最自然的开始是先介绍 Tobit 模型&＃xff0c;再来引入双栏模型。
Tobit 模型又被称为归并回归模型 (censored regression model)&＃xff0c; 根据 limit 的设置分为左归并 (lower censoring) 和右归并 (upper censoring)&＃xff0c;左归并指事先设置一个最小值 A&＃xff0c;当被解释变量低于这个值时则自动等于 A。 如果最低的 limit 为 0 时&＃xff0c;被称为零归并 (zero censoring)。
上面的公式中潜变量
这里以零归并举例&＃xff0c;采用对数似然函数&＃xff0c;估计模型如下&＃xff1a;
其中
Double - hurdle 模型有两个阶段&＃xff0c;这两个阶段分别采用 probit 估计和 tobit 估计&＃xff1a;
在第一个阶段 (hurdle)&＃xff0c;被解释变量 (
在第二个阶段 (hurdle), 被解释变量
上式中&＃xff0c;双栏模型的第二个阶段给
若双栏模型是 upper hurdle 型&＃xff0c;即第二个阶段设置一个最大值
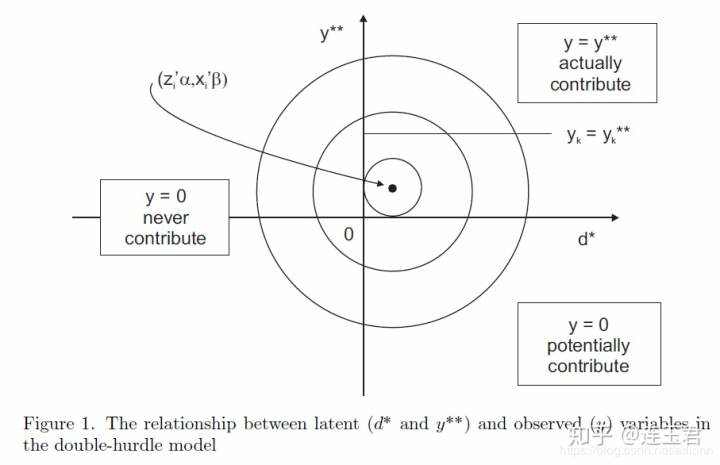
上图中的的同心圆是
如果模型第一阶段&＃xff0c;只有截距而没有解释变量&＃xff0c;
将
连享会 最新专题 直播
我们可以使用 dhreg 命令来实现双栏模型的估计。在 Stata 命令窗口中输入 help dhreg 命令即可查看其完整帮助文件。dhreg 命令的基本语法为&＃xff1a;
dhreg depvar indepvars [if] [in] [, up ptobit hd(varlist) millr]
各项的含义如下&＃xff1a;
depvar: 表示被解释变量&＃xff0c;即最终的可观测的 indepvars&＃xff1a;表示关键的解释变量&＃xff0c;即决定 up&＃xff1a; 将模型设置为右归并&＃xff0c;并且设置 ptobit&＃xff1a; 将双栏模型设置为 p-tobit 模型hd(varlist): 表示第一栏中决定 millr&＃xff1a; 用逆米尔斯比率来控制扰动项的相关性我们通过模拟生成的数据来对 dhreg 命令的使用进行介绍&＃xff0c;下面是数据生成的过程 (DGP)&＃xff1a;
上面第一个公式生成的潜变量
clear all
set obs 1000
set seed 123 // 设置种子&＃xff0c;为了使每次重复模拟过程的结果相同
gen z_i &＃61; uniform() // z_i 服从&＃xff08;0,1)均匀分布
set seed 1234
gen x_i &＃61; uniform()
set obs 1000
set seed 12345
gen e_i2 &＃61; invnormal(uniform()) // e_i2 服从标准正态分布
set seed 12435
gen n_i &＃61; invnormal(uniform())
gen e_i1 &＃61; 0.5*e_i2 &＃43; sqrt(1-0.5*0.5)*n_i
gen d_i &＃61; 0
replace d_i &＃61; 1 if -2 &＃43; 4*z_i &＃43; e_i1 > 0
gen y_i2 &＃61; 0.5 &＃43; 0.3*x_i &＃43; e_i2
gen y_i1 &＃61; 0
replace y_i1 &＃61; y_i2 if y_i2 > 0
gen y_i &＃61; d_i*y_i1
save data_process1.dta, replace // 保存一份模拟数据
数据效果如下&＃xff1a;
use "data_process1.dta", clear
hist y_i if d_i &＃61;&＃61; 1,title(Conditional on passing first hurdle) scheme(sj)
graph save y_i_1.gph, replace
hist y_i ,title(All Data) scheme(sj)
graph save y_i_2.gph, replace
gr combine y_i_1.gph y_i_2.gph
graph save y_i.png, replace
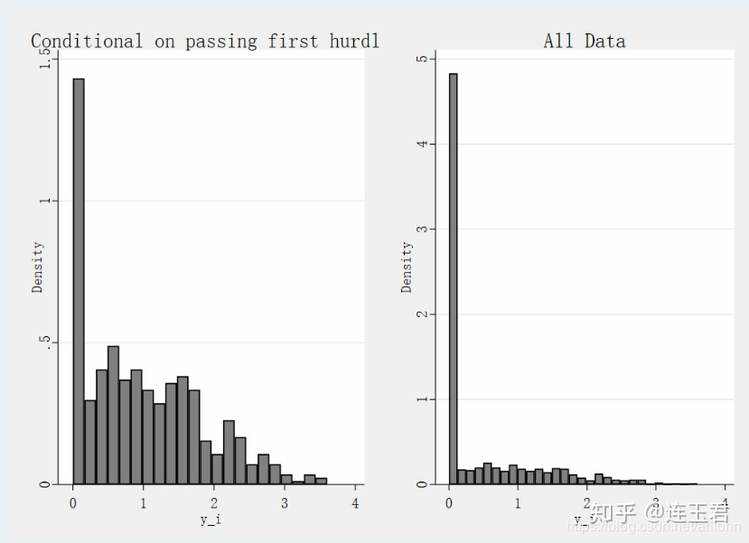
从左图可以看出有很多观测值通过了第一栏(即
我们先进行传统的 tobit 估计, 再使用 dhreg 进行估计&＃xff0c;然后对这两种估计结果进行比较。
. use "data_process1.dta", clear
. tobit y_i x_i, ll(0)
Tobit regression Number of obs &＃61; 1,000Uncensored &＃61; 413
Limits: lower &＃61; 0 Left-censored &＃61; 587upper &＃61; &＃43;inf Right-censored &＃61; 0LR chi2(1) &＃61; 3.49Prob > chi2 &＃61; 0.0619
Log likelihood &＃61; -1129.3849 Pseudo R2 &＃61; 0.0015------------------------------------------------------------------------------y_i | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------&＃43;----------------------------------------------------------------x_i | .3617779 .1939403 1.87 0.062 -.0187992 .7423551_cons | -.4709888 .1194536 -3.94 0.000 -.7053975 -.2365801
-------------&＃43;----------------------------------------------------------------var(e.y_i)| 2.40666 .191884 2.058097 2.814257
------------------------------------------------------------------------------
接着是进行 dhreg 估计&＃xff1a;
dhreg y_i x_i, hd(z_i)(output omitted)maximum likelihood estimates of double hurdle modelN &＃61; 1000
log likelihood &＃61; -984.07209
chi square hurdle equation &＃61; 67.264411
p hurdle equation &＃61; 2.374e-16
chi square above equation &＃61; 4.8518223
p above equation &＃61; .02761694
chi square overall &＃61; 69.895304
p overall &＃61; 6.644e-16--------------------------------------------------------------------------------| coef se z p lower CI upper CI
-------------&＃43;------------------------------------------------------------------
hurdle | z_i | 3.644556 .4443773 8.201488 2.22e-16 2.773592 4.515519_cons | -1.727589 .1522467 -11.3473 7.65e-30 -2.025987 -1.429191
above | x_i | .416768 .189209 2.202685 .0276169 .0459251 .7876109_cons | .5702333 .1428997 3.990444 .0000659 .290155 .8503115
sigma | _cons | 1.053116 .0643765 16.35869 0 .9269402 1.179292
--------------------------------------------------------------------------------
Tobit 模型估计
[注&＃xff1a;我们尝试通过设置不同的种子&＃xff0c;生成不同的随机数&＃xff0c;发现 double hurdle 模型对
Dong and Kaiser (2008) 将双栏模型发展成面板双栏模型&＃xff0c;并使用这个模型对家庭牛奶消费做实证分析。Dong 假设并验证了家庭牛奶消费总的来说由非经济因素和经济因素决定&＃xff0c;非经济因素包括户主年龄、教育、种族背景等&＃xff0c;经济因素包括收入、牛奶的价格等。在一定的时间内&＃xff0c;非经济因素一般不会发生改变&＃xff0c;并且在家庭是否产生购买牛奶的行为中起决定性作用。
在第一个阶段中&＃xff0c;
样本最终的似然对数函数为&＃xff1a;
Stata 中用 xtdhreg 和 boothreg 命令对面板数据进行双栏模型的估计。首先在 Stata 命令窗口中输入 help xtdhreg 命令即可查看其完整帮助文件。xtdhreg 命令的基本语法为&＃xff1a;
xtdhreg depvar indepvars [if] [in] [, up ptobit hd(varlist) uncorr trace ///difficult constraints(numlist)]
各项的含义如下&＃xff1a;
depvar: 表示被解释变量&＃xff0c;即最终的可观测的 indepvars&＃xff1a; 表示关键的解释变量&＃xff0c;即决定 up&＃xff1a; 将模型设置为右归并&＃xff0c;并且设置 ptobit&＃xff1a; 将双栏模型设置为 p-tobit 模型hd(varlist): 表示第一栏中决定 millr&＃xff1a; 用逆米尔斯比率来控制扰动项的相关性uncorr&＃xff1a; 表示第一栏和第二栏中的扰动项不相关trace&＃xff1a; 显示每一次迭代的系数difficult&＃xff1a; 当模型不收敛时&＃xff0c;换用其他替代的算法constraints(numlist)&＃xff1a; 允许对模型进行限制在 Stata 命令窗口中输入 help boothreg 命令即可查看其完整帮助文件。boothreg 命令的基本语法为&＃xff1a;
bootreg depvar indepvars [if] [in] [, up ptobit hd(varlist) millr ///margins(string) seed(integer) reps(integer) strata(varlist) cluster(varlist) ///capt maxiter(integer)]
各项的含义如下&＃xff1a;
depvar: 表示被解释变量&＃xff0c;即最终的可观测的 indepvars&＃xff1a;表示关键的解释变量&＃xff0c;即决定 up&＃xff1a; 将模型设置为右归并&＃xff0c;并且设置 ptobit&＃xff1a; 将双栏模型设置为 p-tobit 模型hd(varlist): 表示第一栏中决定 millr&＃xff1a; 用逆米尔斯比率来控制扰动项的相关性margins(string)&＃xff1a; bootstrep 估计的边际效应seed(integer)&＃xff1a; 设置种子&＃xff0c;为了使结果可重复reps(integer)&＃xff1a; boostrap 重复的次数&＃xff0c;默认是 50 次strata(varlist)&＃xff1a; 进行分层抽样capt&＃xff1a; 自动忽略不收敛的情况maxiter(integer)&＃xff1a; 设置迭代的最多次数&＃xff0c;默认为 50本小节我们先模拟生成面板数据&＃xff0c;然后再利用生成的数据进行模型估计。
面板数据的个体为
clear all
set obs 2000
set seed 10011979
gen z_i &＃61; uniform()
set seed 1111122
gen u_i &＃61; rnormal(0, 3)
set seed 1222222
gen n_i &＃61; rnormal(0,3)
gen e_i1 &＃61; 0.9*u_i &＃43; sqrt(1-0.9^2)*n_i/* 面板数据生成过程 */
gen d_i &＃61; 0
replace d_i &＃61; 1 if -2 &＃43; 4*z_i &＃43; e_i1 > 0
gen id &＃61; _n
expand 5 // 将 T 设置为 5 期
bys id: gen t &＃61; _n
xtset id t
bysort id (t): gen x_it &＃61; rnormal(0,1) &＃43; rnormal(0,1) if _n&＃61;&＃61;1
bysort id (t): replace x_it &＃61; .8 * x_it[_n-1] &＃43; rnormal(0,1) if _n!&＃61;1
gen e_i2 &＃61; rnormal(0,1)
gen y_it2 &＃61; 0.5 &＃43; 0.3*x_it &＃43; u_i &＃43; e_i2
corr e_i2 u_i // 检查e_i2和u_i的相关性
gen y_it1 &＃61; 0
replace y_it1 &＃61; y_it2 if y_it2 > 0
gen y_it &＃61; y_it1*d_i
save data_process2.dta, replace //保存模拟数据
xtdhreg 命令进行双栏估计的结果如下&＃xff1a;use data_process2.dta, clear
help mdraws // 进行 xtdhreg 估计前&＃xff0c;需要装&＃96;mdraws&＃96;包
xtdhreg y_it x_it, hd(z_i)
(output omitted)
Number of obs &＃61; 10,000
Wald chi2(1) &＃61; 46.82
Log likelihood &＃61; -9013.4217 Prob > chi2 &＃61; 0.0000------------------------------------------------------------------------------Coef. Std. Err. z P>|z| [95% Conf. Interval]
----------------&＃43;-------------------------------------------------------------
hurdle z_i | .6908215 .1009566 6.84 0.000 .4929501 .8886929_cons | -.2702063 .0611108 -4.42 0.000 -.3899812 -.1504313
----------------&＃43;-------------------------------------------------------------
above x_it | .2971716 .0162833 18.25 0.000 .2652569 .3290863_cons | 3.887898 .1050517 37.01 0.000 3.682001 4.093796
----------------&＃43;-------------------------------------------------------------
sigma_u _cons | 3.249278 .0942043 34.49 0.000 3.064641 3.433915
----------------&＃43;-------------------------------------------------------------
sigma_e _cons | .9920639 .012312 80.58 0.000 .9679329 1.016195
----------------&＃43;-------------------------------------------------------------
transformed_rho _cons | -.9211924 .0730788 -12.61 0.000 -1.064424 -.7779606
------------------------------------------------------------------------------rho: tanh([transformed_rho]_cons)------------------------------------------------------------------------------| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------&＃43;----------------------------------------------------------------rho | -.726461 .0345118 -21.05 0.000 -.7941029 -.6588192
------------------------------------------------------------------------------separate Wald tests for joint significance of all explanatory variablesnoteif you use factor variables, i.e. the i., c., # and ## notation, you must runthe Wald test by hand. For detail see help fileestimates of joint significancechi square hurdle equation &＃61; 46.823275
p hurdle equation &＃61; 7.769e-12
chi square above equation &＃61; 333.06554
p above equation &＃61; 2.066e-74
chi square overall &＃61; 376.42223
p overall &＃61; 1.824e-82
用 bootdreg 命令进行双栏模型估计结果如下&＃xff1a;
bootdhreg y_it x_it, hd(z_i) cluster(id) capt
(output omitted)
maximum likelihood estimates of double hurdle modelN &＃61; 10000
log likelihood &＃61; -14962
chi square hurdle equation &＃61; 140.17438
p hurdle equation &＃61; 2.438e-32
chi square main equation &＃61; 140.17438
p main equation &＃61; 2.438e-32
chi square overall &＃61; 442.19897
p overall &＃61; 9.500e-97
bootstrap results------------------------------------------------------------------------------| coef se p lowciz upciz lowcip upcip
------------&＃43;-----------------------------------------------------------------
hurdle | z_i | 1.002614 .122 0 .7634344 1.241794 .7598894 1.346414_cons | -.4531903 .072 0 -.5948118 -.3115688 -.6363495 -.2646514
main | 0 x_it | .3388443 .052 0 .2370221 .4406664 .2289405 .4781399_cons | 2.279919 .132 0 2.020481 2.539356 1.868922 2.511813
sigma | _cons | 2.583072 .095 0 2.396594 2.76955 2.401081 2.808727
------------------------------------------------------------------------------
从回归结果可以看出&＃xff0c;xtdhreg 和 bootdhreg 对样本的
相关课程
连享会-直播课 上线了&＃xff01;http://lianxh.duanshu.com免费公开课&＃xff1a;
Note: 助教招聘信息请进入「课程主页」查看。
因果推断-内生性 专题 ⌚ 2020.11.12-15
主讲&＃xff1a;王存同 (中央财经大学)&＃xff1b;司继春(上海对外经贸大学)课程主页&＃xff1a;https://gitee.com/arlionn/YG | 微信版
空间计量 专题 ⌚ 2020.12.10-13
主讲&＃xff1a;杨海生 (中山大学)&＃xff1b;范巧 (兰州大学)课程主页&＃xff1a;https://gitee.com/arlionn/SP | 微信版
关于我们
连享会小程序&＃xff1a;扫一扫&＃xff0c;看推文&＃xff0c;看视频……
扫码加入连享会微信群&＃xff0c;提问交流更方便
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有