做数学建模不得不会的数据特征分析对比分析

对比分析主要用于对两个互相联系的指标进行比较，包括绝对数比较（相减）/相对数比较（相除），结构分析，比例分析，空间比较分析，动态对比分析等，这篇博客来一一写一下分析方法

首先引入所需模块

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline


1.绝对数比较（相减）

这种方法相互对比的指标在量级上不能相差过大，不然得不到明显的对比结果。
创建数据，生成30天内的A/B产品的日销售额

data = pd.DataFrame(np.random.rand(30,2)*1000,
columns = ['A_sale','B_sale'],
index = pd.period_range('20170601','20170630'))#pandas中与时间相关的函数
print(data.head())


数据展示

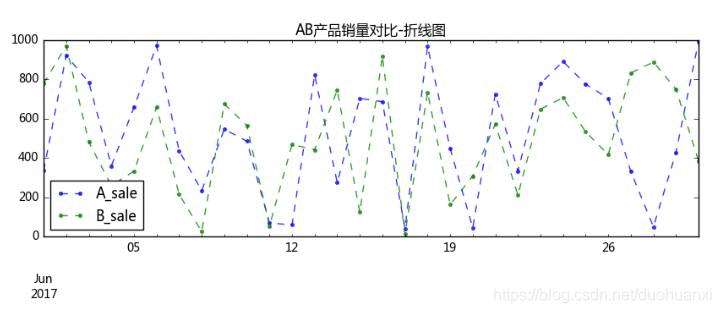
（2）折线图比较

data.plot(kind='line',
style = '--.',
alpha = 0.8,
figsize = (10,3),
title = 'AB产品销量对比-折线图')


输出结果：

（3）多系列柱状图对比


data.plot(kind = 'bar',
width = 0.8,
alpha = 0.8,
figsize = (10,3),
title = 'AB产品销量对比-柱状图')


输出结果：

（4）柱状图，堆叠图对比

创建堆叠图

ax1 = fig3.add_subplot(2,1,1)
x = range(len(data))
y1 = data['A_sale']
y2 = -data['B_sale']
plt.bar(x,y1,width = 1,facecolor = 'yellowgreen')
plt.bar(x,y2,width = 1,facecolor = 'lightskyblue')
plt.title('AB产品销量对比-堆叠图')
plt.grid()
plt.xticks(range(0,30,6))
ax1.set_xticklabels(data.index[::6])


输出结果：

（5）差值折线图对比

ax2 = fig3.add_subplot(2,1,2)
y3 = data['A_sale']-data['B_sale']#产品A与B差值
plt.plot(x,y3,'--go')
plt.axhline(0,hold=None,color='r',linestyle="--",alpha=0.8) # 添加y轴参考线
plt.grid()
plt.title('AB产品销量对比-差值折线')
plt.xticks(range(0,30,6))
ax2.set_xticklabels(data.index[::6])


输出结果：

2.相对数比较（相除）

相对数比较主要用于有联系的指标综合计算后的对比，数值为相对数，主要对比方法有结构分析、比例分析、空间比较分析、动态对比分析、计划完成度分析等

（1）结构分析
结构分析是在分组的基础上，对各组总量指标与总体的总量指标进行对比，计算出各组数量在总量中所占的比重，它可以反映总体的内部结构
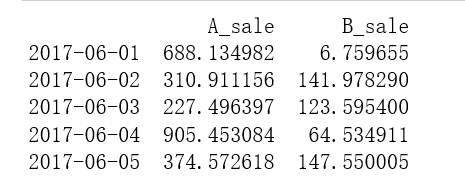
首先创建数据，生成30天内A/B产品的日销售额
为了对比效果，这里我们设置A与B的数量级是不同的

data = pd.DataFrame({ 'A_sale':np.random.rand(30)*1000,
'B_sale':np.random.rand(30)*200},
index = pd.period_range('20170601','20170630'))
print(data.head())


输出结果：

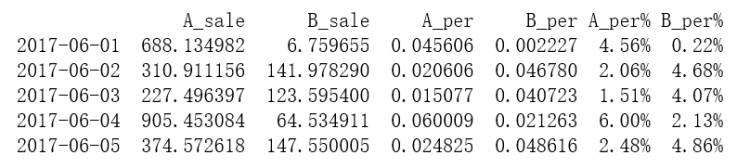
计算A、B产品每一天的营收占比，并转换为百分数

data['A_per'] = data['A_sale'] / data['A_sale'].sum()
data['B_per'] = data['B_sale'] / data['B_sale'].sum()
data['A_per%'] = data['A_per'].apply(lambda x: '%.2f%%' % (x*100))
data['B_per%'] = data['B_per'].apply(lambda x: '%.2f%%' % (x*100))


数据展示：

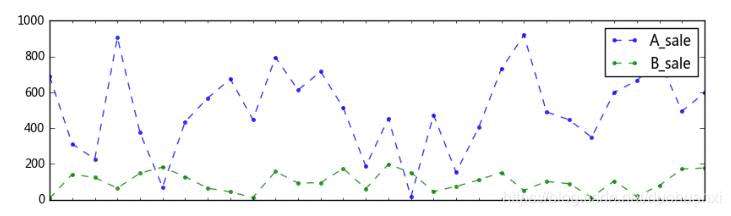
看一下销售量情况

data[['A_sale','B_sale']].plot(kind='line',style = '--.',alpha = 0.8,ax=axes[0])
axes[0].legend(loc = 'upper right')


绘制结果：

再通过销售额占比来看一下售卖情况

data[['A_per','B_per']].plot(kind='line',style = '--.',alpha = 0.8,ax=axes[1])
axes[1].legend(loc = 'upper right')


绘制结果：

只看销售量的对比我们难以看出结构性的变化，通过销售额会比较容易看到售卖情况的对比。
（2）比例分析
在分组的基础上将总体不同部分的指标数值进行对比，其相对指标一般称为‘比例相对数’，比例相对数是总体中某一部分数值/总体中另一部分数值。

首先生成数据，生成某人一年内的消费、工资薪水情况，其中消费按照2000-3000/月随机生成，工资按照5000-5500/月随机生成

data = pd.DataFrame({ 'consumption':np.random.rand(12)*1000 + 2000,
'salary':np.random.rand(12)*500 + 5000},
index = pd.period_range('2017/1','2017/12',freq = 'M'))
print(data.head())


数据结果：

计算比例相对数，消费与收入的比值

data['c_s'] = data['consumption'] / data['salary']
print(data.head())


绘制面积图观察结果

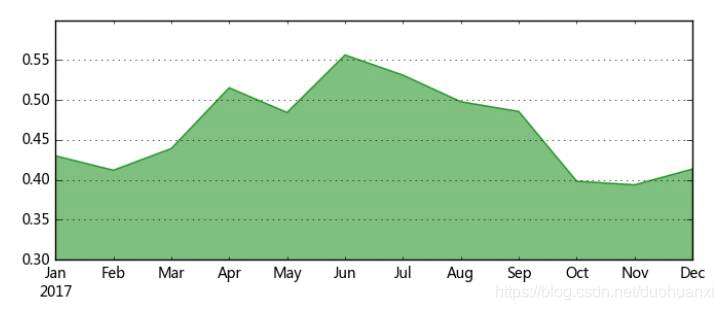
（3）空间比较分析
包括横向对比分析和纵向对比分析。
横向对比分析是同类现象在同一时间不同空间的指标数值进行对比，可以反应同类现象在不同空间上的差异程度和现象发展不平衡的状况，空间比较数为 甲空间某一现象的数值/乙空间同类现象的数值，比如从绝对数来看，我国经济总量世界第一，但是从人均水平来看却是另一回事

首先生成数据，30天内A/B/C/D四个产品的销售情况，不同产品我们设置销售量级不同

data = pd.DataFrame({ 'A':np.random.rand(30)*5000,
'B':np.random.rand(30)*2000,
'C':np.random.rand(30)*10000,
'D':np.random.rand(30)*800},
index = pd.period_range('20170601','20170630'))
print(data.head())


数据展示：

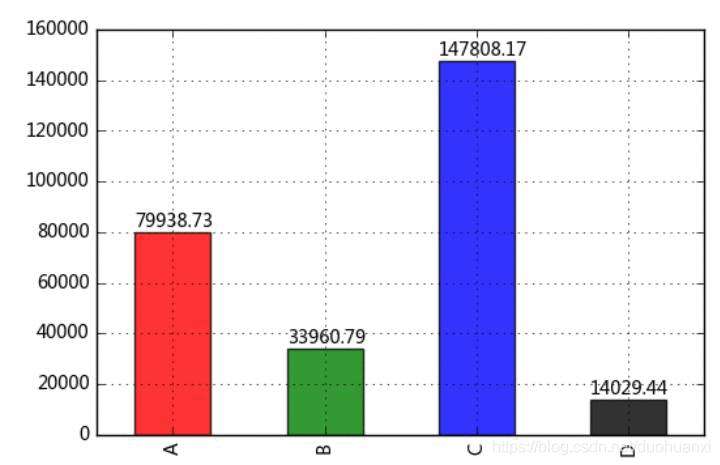
通过柱状图做横向比较，比较四个产品销售额

data.sum().plot(kind = 'bar',color = ['r','g','b','k'], alpha = 0.8, grid = True)
for i,j in zip(range(4),data.sum()):
plt.text(i-0.25,j+2000,'%.2f' % j, color = 'k')


输出结果：

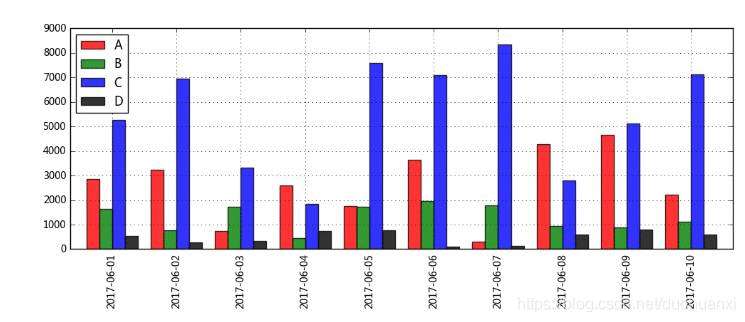
再通过柱状图，横向比较前十天4个产品的销售额

data[:10].plot(kind = 'bar',color = ['r','g','b','k'], alpha = 0.8, grid = True, figsize = (12,4),width = 0.8)


绘制结果：

再来一个小tips

# 关于同比与环比
# 同比 → 产品A在2015.3和2016.3的比较（相邻时间段的同一时间点）
# 环比 → 产品A在2015.3和2015.4的比较（相邻时间段的比较）
# 如何界定“相邻时间段”与“时间点”，决定了是同比还是环比


看完以上横向对比，再来看一下纵向对比，也称动态对比分析，它是同一现象在不同时间上的指标数值进行对比，反应现象的数量随着时间推移而发展变动的程度及趋势，最基本分方法是计算动态相对数，反应发展速度
动态相对数（发展速度）=某一现象的报告期数值/同一现象的基期数值
基期是用来比较的基础时期，报告期是所要研究的时期，又称计算期

首先创建数据，生成30天内A产品的销售情况

data = pd.DataFrame({ 'A':np.random.rand(30)*2000+1000},
index = pd.period_range('20170601','20170630'))
print(data.head())


数据展示：

假设基期销售额为1000，计算累积增长量和逐期增长量

data['base'] = 1000 # 假设基期销售额为1000，后面每一天都为计算期
data['l_growth'] = data['A'] - data['base'] # 累计增长量 = 报告期水平 - 固定基期水平
data['z_growth'] = data['A'] - data.shift(1)['A'] # 逐期增长量 = 报告期水平 - 报告期前一期水平
data[data.isnull()] = 0 # 替换缺失值


通过绘制折线图查看增长量情况

data[['l_growth','z_growth']].plot(figsize = (10,4),style = '--.',alpha = 0.8)
plt.axhline(0,hold=None,color='r',linestyle="--",alpha=0.8) # 添加y轴参考线
plt.legend(loc = 'lower left')
plt.grid()


绘制结果：

再来看一下发展速度

data['lspeed'] = data['l_growth'] / data['base'] # 定期增长速度
data['zspeed'] = data['z_growth'] / data.shift(1)['A'] # 环比增长速度
data[['lspeed','zspeed']].plot(figsize = (10,4),style = '--.',alpha = 0.8)
plt.axhline(0,hold=None,color='r',linestyle="--",alpha=0.8) # 添加y轴参考线
plt.grid()


绘制结果：

好的，就到这里了

关注欢喜，走向成功~