支持向量机(SVM)的数学原理

支持向量机(SVM)的数学原理

线性可分数据

数据抽象为不同特征值作为不同维度的向量后&＃xff0c;将分布在高维空间中&＃xff0c;高维空间中的数据&＃xff0c;如果能用一个维平面分开不同标签的数据&＃xff0c;则称这组数据线性可分。

高维空间中的距离

如果高维空间中的数据线性可分&＃xff0c;我们希望尽量用一个平面把两组数据分得开一点&＃xff0c;那么我们需要引入度量&＃xff0c;下面推导高维空间中的距离。
　　

求解分隔平面的优化问题

考虑线性可分的数据&＃xff0c;我们为了分得开一点&＃xff0c;需要转化为以下优化问题&＃xff0c;由于优化问题是一个带约束的最值问题&＃xff0c;所以可以考虑使用拉格朗日乘子法求出平面参数符合的必要条件。
　　

求解时&＃xff0c;可以转化为对偶问题求解。(对偶问题以及KKL条件可以参考拉格朗日乘子法)

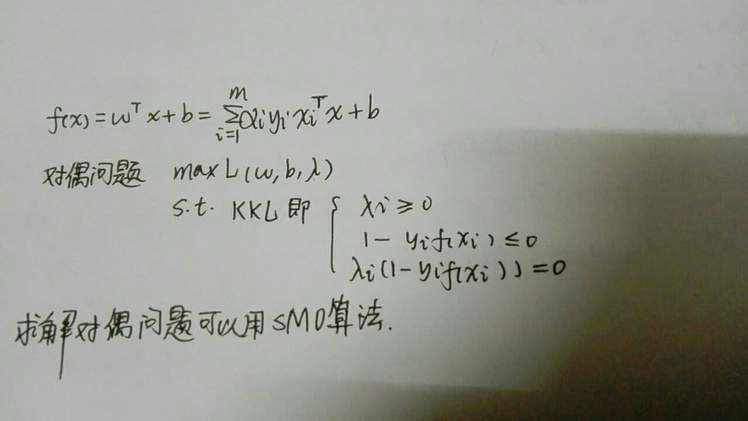
用SMO算法求解对偶问题

当优化变量很多的时候&＃xff0c;可以先固定某些变量仅仅允许两个变量变动&＃xff0c;且由于约束条件&＃xff0c;事实上变成了一元函数&＃xff0c;再对这个一元函数求最大值&＃xff0c;而这个求解的难度会小很多&＃xff0c;有闭合形式的代数解。
　　那么一次固定调整过程后&＃xff0c;优化值变大。重复迭代这一过程即可。

当然&＃xff0c;因为我学习的时候仅仅关心数学原理&＃xff0c;并不关心实现细节。所以没有深究选择变量的原则&＃xff0c;事实上选择变量需要用启发式搜索&＃xff0c;也就是说有某种原则&＃xff0c;使得选择的变量可以令值上升尽量多。每次更新还需要更新阈值b保证KKT条件。

选择核函数处理线性不可分数据

当线性不可分的时候&＃xff0c;需要选择合适的核函数&＃xff0c;即认为分隔在核函数作用后的平面中进行:wTΦ(x)&＃43;b&＃61;0w^T\Phi(x)&＃43;b&＃61;0wTΦ(x)&＃43;b&＃61;0。

那么我们实际不必求解$\Phi (x)$&＃xff0c;只需要求解Φ(xi)TΦ(xj)\Phi(x_i)^T\Phi(x_j)Φ(xi​)TΦ(xj​)即可。

关于核函数的选择&＃xff0c;不同选择对应不同核&＃xff0c;有线性核&＃xff0c;多项式核&＃xff0c;高斯(对应RBF神经网络)&＃xff0c;拉普拉斯核&＃xff0c;sigmoids核(对应单层MLP神经网络)。

软间隔和正则化

因为允许的噪音和反例存在&＃xff0c;所以约束不应该是硬约束&＃xff0c;而是软约束&＃xff0c;也就是违反会获得惩罚&＃xff0c;但是违反这个0/1函数不可导&＃xff0c;所以用对应的可导函数代替。这就是软间隔。
　　
　　正则化为了降低结构风险&＃xff0c;构造关于参数大小的惩罚项。
　　
　　这两个技术是SVM中常见的技术。

支持向量

事实上由于很多点比较远&＃xff0c;所以在KKT条件中&＃xff0c;λi\lambda_iλi​对应取0&＃xff0c;而分隔平面不会经过它们&＃xff0c;所以可以忽略它们降低复杂度。也就是说&＃xff0c;学习的时候只学习最容易混淆的&＃xff0c;最靠近分隔面的。那么这些留下来的向量称为支持向量。支持向量的思想可以减少运算量和复杂度。

结语

我学习的时候着重关注支持向量机的数学原理&＃xff0c;所以前面部分推导总结较仔细&＃xff0c;后面具体实现的知识简单地过一遍。
　　
　　下面解释一下&＃xff0c;支持向量机名字&＃xff0c;顾名思义:
　　支持向量(Support Vector): 高维空间内平面分隔数据点向量&＃xff0c;保留支持向量。
　　机(Machine): 二分判定机器