正则化项与归一化

http://blog.csdn.net/gshgsh1228/article/details/52199870转载

 首先了解一下正则性&＃xff08;regularity&＃xff09;&＃xff0c;正则性衡量了函数光滑的程度&＃xff0c;正则性越高&＃xff0c;函数越光滑。&＃xff08;光滑衡量了函数的可导性&＃xff0c;如果一个函数是光滑函数&＃xff0c;则该函数无穷可导&＃xff0c;即任意n阶可导&＃xff09;。

       正则化是为了解决过拟合问题。在Andrew Ng的机器学习视频中有提到&＃xff08;详见http://www.cnblogs.com/jianxinzhou/p/4083921.html&＃xff09;。解决过拟合的两种方法&＃xff1a;

     方法一&＃xff1a;尽量减少选取变量的数量。人工检查每一个变量&＃xff0c;并以此来确定哪些变量更为重要&＃xff0c;然后&＃xff0c;保留那些更为重要的特征变量。显然这种做法需要对问题足够了解&＃xff0c;需要专业经验或先验知识。因此&＃xff0c;决定哪些变量应该留下不是一件容易的事情。此外&＃xff0c;当你舍弃一部分特征变量时&＃xff0c;你也舍弃了问题中的一些信息。例如&＃xff0c;也许所有的特征变量对于预测房价都是有用的&＃xff0c;我们实际上并不想舍弃一些信息或者说舍弃这些特征变量。

最好的做法是采取某种约束可以自动选择重要的特征变量&＃xff0c;自动舍弃不需要的特征变量。

    方法二&＃xff1a;正则化。采用正则化方法会自动削弱不重要的特征变量&＃xff0c;自动从许多的特征变量中”提取“重要的特征变量&＃xff0c;减小特征变量的数量级。这个方法非常有效&＃xff0c;当我们有很多特征变量时&＃xff0c;其中每一个变量都能对预测产生一点影响。正如在房价预测的例子中看到的那样&＃xff0c;我们可以有很多特征变量&＃xff0c;其中每一个变量都是有用的&＃xff0c;因此我们不希望把它们删掉&＃xff0c;这就导致了正则化概念的发生。

正则化的作用&＃xff1a;

&＃xff08;1&＃xff09;防止过拟合&＃xff1b;

&＃xff08;2&＃xff09;正则化项的引入其实是利用了先验知识&＃xff0c;体现了人对问题的解的认知程度或者对解的估计&＃xff1b;例如正则化最小二乘问题如下&＃xff1a;

N表示所有样本的数量&＃xff0c;n表示参数的个数。

lambda合适即可&＃xff0c;太大又会导致欠拟合。

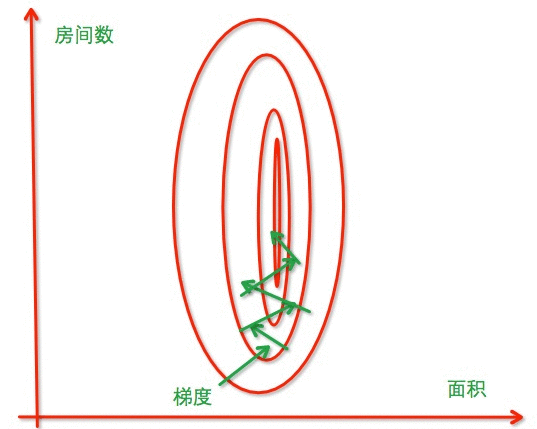
归一化&＃xff1a;加快收敛速度&＃xff0c;尽快找到最优值

我们在对数据进行分析的时候&＃xff0c;往往会遇到单个数据的各个维度量纲&＃xff08;度量单位&＃xff09;不同的情况&＃xff0c;比如对房子进行价格预测的线性回归问题中&＃xff0c;我们假设房子面积&＃xff08;平方米&＃xff09;、年代&＃xff08;年&＃xff09;和几居室&＃xff08;个&＃xff09;三个因素影响房价&＃xff0c;其中一个房子的信息如下&＃xff1a;

• 面积(S)&＃xff1a;150 平方米
• 年代(Y)&＃xff1a;5 年
• 

  

  

•