当前位置: 开发笔记 > 后端 > 正文

正交性原理与维纳霍夫（正则）方程

作者：拍友2502906483 | 来源：互联网 | 2023-07-13 10:44

有期望信号d（n），纯净信号x（n），以及噪声信号g（n）;有滤波

有期望信号d&＃xff08;n&＃xff09;&＃xff0c;纯净信号x&＃xff08;n&＃xff09;&＃xff0c;以及噪声信号g&＃xff08;n&＃xff09;;

有滤波器h&＃xff08;m&＃xff09;,以及滤波器输出信号y&＃xff08;n&＃xff09;&＃xff0c;滤波器输出纯净信号x的估计值y&＃xff0c;并且使y与x误差的期望为0.

$\begin{aligned} y(n)&&＃61;\sum_{m&＃61;0}^{\infty }h(m)\cdot d(n-m)\\&&＃61;\sum_{m&＃61;0}^{\infty }h(n-m)\cdot d(m) \\&&＃61;h(n)*d(n)\\\end{aligned}$

$d(n)&＃61;x(n)&＃43;g(n)$

$e(n)&＃61;x(n)-y(n)$

$E\left \{ \left | e(n) \right |^{2} \right \}$

$R_{xy}(m-j)&＃61;E\left \{ x(n-j)\cdot y(n-m) \right \}$ &＃xff08;相关性&＃xff09;

根据最小均方差准则设计滤波器,滤波器设计问题转为 $E\left \{ \left | e(n) \right |^{2} \right \}&＃61;E\left \{ \left ( x(n)-\sum_{m&＃61;0}^{\infty }h(m)\cdot d(n-m) \right )^{2} \right \}$ 函数求驻点的问题&＃xff0c;在驻点处 $E\left \{ \left | e(n) \right |^{2} \right \}$ 能够取得极值&＃xff0c;如果能证明该式有连续二阶偏导&＃xff0c;且得到的hesse矩阵正定&＃xff0c;则求取的极值点就是该式的严格局部极小值点&＃xff0c;这实际上就是一个非线性规划中的无约束最优化问题&＃xff0c;进一步如果能证明 $E\left \{ \left | e(n) \right |^{2} \right \}$ 是凸的&＃xff0c;那么该式局部极小值就是全局极小值。h(j)为变量&＃xff0c;函数对h(j)求偏导,当求偏导结果为0时候&＃xff0c;均方差取得最小值&＃xff0c;此时的滤波器权值为最优滤波器权值&＃xff1a;

$\frac{\partial E\left \{ \left | e(n) \right |^{2} \right \}}{\partial h(j)}\\ &＃61;\frac{\partial E\left \{ (x(n)-h(n)*d(n))^{2} \right \}}{\partial h(j)}\\ &＃61;\frac{\partial E\left \{ x^{2}(n)-2x(n)\cdot h(n)*d(n)&＃43;\left (h(n)*d(n) \right )^{2}\right \} }{\partial h(j)}\\ &＃61;\frac{\partial E\left \{ x^{2}(n) \right \}}{\partial h(j)}-E\left \{ 2x(n)\cdot d(n-j) \right \}&＃43;2\cdot \left \{ \sum_{m&＃61;0}^{n}h(m)\cdot E(x(n-m)\cdot d(n-j)) \right \}\\ &＃61;0&＃43;2R_{dx}(j)-2\sum_{m&＃61;0}^{n}h(m)\cdot R_{dd}(j-m)\\ &＃61;2R_{dx}(j)-2h(j)*R_{dd}(j)$

当以上式子&＃61;0时&＃xff0c;整理得到维纳霍夫方程&＃xff1a;

$R_{dx}(j)&＃61;h(j)*R_{dd}(j)$

分别对等式两边进行傅里叶变换&＃xff0c;将时域计算转到频域内处理&＃xff0c;时域内的相关转到频域内表现为(互)功率谱&＃xff0c;时域内的卷积转换到频域内表现为相乘&＃xff1a;

$P_{dx}(\omega )&＃61;H(\omega )\cdot P_{dd}(\omega )$

整理得维纳滤波器权系数计算公式&＃xff1a;

$H(\omega )&＃61;\frac{P_{dx}(\omega )}{P_{dd}(\omega )}$

同时注意到&＃xff1a;

$\frac{\partial E\left \{ x^{2}(n)-2x(n)\cdot h(n)*d(n)&＃43;\left (h(n)*d(n) \right)^{2}\right \} }{\partial h(j)}\\ &＃61;\frac{E \partial \left \{ x^{2}(n)-2x(n)\cdot h(n)*d(n)&＃43;(h(n)*d(n)) ^{2}\right \} }{\partial h(j)}\\ &＃61;E\left \{ 0-2x(n)\cdot d(n-j)&＃43;2y(n)\cdot d(n-j) \right \}\\ &＃61;-2E\left \{ e(n)\cdot d(n-j) \right \}$

当上式&＃61;0时候&＃xff0c;经过整理即得到正交性原理:当&＃61;0时候&＃xff0c;均方差取得最小值

也就是说正交性原理与维纳霍夫方程是同一个条件 $E\left \{ \left | e(n) \right |^{2} \right \}&＃61;0$ 的两种表达方式&＃xff0c;将求解的结果写成期望的形式得到的就是正交性原理&＃xff0c;写成相关的形式就是维纳霍夫方程。

以上&＃xff0c;我们虽然得到了维娜霍夫方程的表达形式。但是在设计维纳滤波器的过程中&＃xff0c;目标信号x无法获取&＃xff0c;因此就无法得到纯净信号x与期望信号d之间的相关向量&＃xff0c;也就是说上述维娜霍夫方程是无法应用在实际信号处理过程之中的。对于这个问题我们可以通过使用替代的方法对以上方程进行改造。我们将纯净信号表示成期望信号d与噪声g的差值&＃xff0c;同时我们假设纯净信号x与噪声g之间相互独立&＃xff0c;这样我们就能将期望信号d与纯净信号x之间的相关性重新表示如下&＃xff1a;

$R{_d_x} &＃61; E[d(n)x(n)]\\ &＃61; E[d(n)*[d(n)-g(n)]]\\ &＃61; E[d(n)d(n)] - E[[x(n)&＃43;g(n)]*g(n)]$

因为 x与g相互独立&＃xff0c;所以Rxg &＃61; 0&＃xff0c;带入上式

$R{_d_x} &＃61; E[d(n)*d(n)]-E[g(n)*g(n)]\\&＃61;R{_d_d}-R{_g_g}$

重新整理维纳霍夫方程&＃xff0c;得到如下形式&＃xff1a;

$R_{dd} - R_{gg}&＃61;h(j)*R_{dd}(j)$

重新整理维纳滤波器的形式

$H(\omega )&＃61;\frac{P_{dd}(\omega )-P_{gg}(\omega )}{P_{dd}(\omega )}$

根据公式可以看出&＃xff0c;维纳滤波器的系数在特定条件下&＃xff08;滤波器的输入纯净信号与输入的噪声不想关&＃xff09;可以通过输入的期望信号d和噪声功率完全获得&＃xff0c;而且噪声可以通过设置前端无语音段的平均功率作为初始条件然后在每一次处理过程中迭代获得。

概念补充&＃xff1a;

希尔伯特空间&＃xff1a;属于泛函分析的核心概念&＃xff0c;是一个满足多项式计算法则、具有范数概念&＃xff08;距离的一个子概念&＃xff09;、满足内积运算&＃xff0c;并具有完备性&＃xff08;空间内的极限运算结果仍落在空间范围内&＃xff09;特点的特殊空间。

一个抽象的希尔伯特空间中的元素往往被称为向量&＃xff0c;这个希尔伯特空间则可以代表一个系统&＃xff0c;每个希尔伯特空间内都有一族标准正交基&＃xff0c;空间内的任何元素都可以用这族标准正交基或其倍数的和表示。

希尔伯特空间元素 &＃xff1a;

$a&＃61; \left ( a1,a2,...,an \right )$

希尔伯特空间元素&＃xff1a;

$b&＃61;\left ( b1,b2,...,bn \right )$

两元素的内积&＃xff1a;

$\left \langle a,b \right \rangle&＃61;a\cdot b^{T}&＃61;a1\cdot b1&＃43;a2\cdot b2&＃43;...&＃43;an\cdot bn$

同时&＃xff0c;如果 &＃61; 0,则认为元素a与元素b正交。

a的范数&＃xff08;类似于线性空间中的距离定义&＃xff09;

$\left \| a \right \|&＃61;\sqrt{\left \langle a,a \right \rangle}$

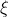正交性原理&＃xff1a;当> &＃61; 0时候&＃xff0c;由 $\eta_{i}$ 估计出来的 $\hat{\xi }&＃61;\sum a_{i}\cdot \eta _{i}$ 与原来的 $\xi$ 值之间的均方误差e最小。

关于共轭的一个小知识点&＃xff1a;

若 $X_{n}\cdot Y_{n}^{*}&＃61;0$ &＃xff0c;则 $X_{n}^{*}\cdot Y_{n}&＃61;0$ &＃xff08;知识点1&＃xff09;

$X_{n}&＃61;\left | a \right |\cdot e^{j\theta_{1}}$

$Y_{n}&＃61;\left | b \right |\cdot e^{j\theta _{2}^{}}$

$X_{n}\cdot Y_{n}^{*} &＃61;\left | a\cdot b \right |\cdot e^{j\left ( \theta _{1} -\theta _{2}\right )} &＃61;\left | a\cdot b \right |\cdot cos(\theta _{1}-\theta _{2})&＃43;\left | a\cdot b \right |\cdot sin(\theta _{1}-\theta _{2})\cdot j$

$X_{n}^{*}\cdot Y_{n} &＃61;\left | a\cdot b \right |\cdot e^{j\left ( \theta _{2} -\theta _{1}\right )} &＃61;\left | a\cdot b \right |\cdot cos(\theta _{2}-\theta _{1})&＃43;\left | a\cdot b \right |\cdot sin(\theta _{2}-\theta _{1})\cdot j$

要想式子等于0&＃xff0c;实部、虚部必须同时为0&＃xff0c;分别对比以上式子中的虚部与实部&＃xff0c;可证知识点1

$X_{n}\cdot Y_{n}^{*}&＃61;\left (X_{n}^{*}\cdot Y_{n} \right )^{*}$

推荐阅读

算法
理解与实现动态赋值

本文深入探讨了动态赋值的概念及其在编程实践中的应用，特别是通过Java代码示例来展示如何利用循环结构动态地为数组分配值。 ... [详细]

蜡笔小新 2024-11-22 14:17:01
go
吴石访谈：腾讯安全科恩实验室如何引领物联网安全研究

腾讯安全科恩实验室曾两次成功破解特斯拉自动驾驶系统，并远程控制汽车，展示了其在汽车安全领域的强大实力。近日，该实验室负责人吴石接受了InfoQ的专访，详细介绍了团队未来的重点方向——物联网安全。 ... [详细]

蜡笔小新 2024-11-22 13:27:32
python
变量间相关性分析

本文探讨了如何通过统计方法评估两个变量之间的关系强度，重点介绍了皮尔森相关系数的计算及其应用。除了数学公式外，文章还提供了Python编程实例，展示如何利用实际数据集（如泰坦尼克号乘客数据）进行相关性检验。 ... [详细]

蜡笔小新 2024-11-22 12:53:03
python
OpenCV中的霍夫圆检测技术解析

本文详细介绍了如何使用OpenCV库中的HoughCircles函数实现霍夫圆检测，并提供了具体的代码示例及参数解释。 ... [详细]

蜡笔小新 2024-11-22 12:17:05
java
解决Android Studio意外崩溃及重启后Import错误问题

本文提供了一种有效的方法来解决当Android Studio因电脑意外重启而导致的所有import语句出现错误的问题。通过清除缓存和重建项目结构，可以快速恢复开发环境。 ... [详细]

蜡笔小新 2024-11-22 11:53:00
struct
网络流24题——试题库问题

题目描述：假设一个试题库中有n道试题。每道试题都标明了所属类别。同一道题可能有多个类别属性。现要从题库中抽取m道题组成试卷。并要求试卷包含指定类型的试题。试设计一个满足要求的组卷算 ... [详细]

蜡笔小新 2024-11-22 11:33:55
python
基于OpenCV和Python的边缘检测与四点变换实现

本文介绍了如何利用OpenCV库进行图像的边缘检测，并通过Canny算法提取图像中的边缘。随后，文章详细说明了如何识别图像中的特定形状（如矩形），并应用四点变换技术对目标区域进行透视校正。 ... [详细]

蜡笔小新 2024-11-22 11:31:52
python
算法解析：最大连续子数组和

本文将探讨一个经典算法问题——最大连续子数组和。我们将从问题定义出发，逐步深入理解其背后的逻辑，并通过实例分析加深理解。 ... [详细]

蜡笔小新 2024-11-21 20:21:35
java
H5技术实现经典游戏《贪吃蛇》

本文将分享一个使用HTML5技术实现的经典小游戏——《贪吃蛇》。通过H5技术，我们将探讨如何构建这款游戏的两种主要玩法：积分闯关和无尽模式。 ... [详细]

蜡笔小新 2024-11-21 20:16:59
python
Python算法实践：多维缩放技术的应用

本文介绍了多维缩放（MDS）技术，这是一种将高维数据映射到低维空间的方法，通过保持原始数据间的关系，以便于可视化和分析。文章详细描述了MDS的原理和实现过程，并提供了Python代码示例。 ... [详细]

蜡笔小新 2024-11-21 20:04:27
python
Spring 事件监听机制详解与应用

本文详细介绍了如何在Spring框架中设置事件发布器、定义事件监听器及响应事件的具体步骤。通过实现ApplicationEventPublisherAware接口来创建事件发布器，利用ApplicationEvent类定义自定义事件，并通过ApplicationListener接口来处理这些事件。 ... [详细]

蜡笔小新 2024-11-21 19:17:55
python
TCP协议中的可靠传输机制分析

本文深入探讨了TCP协议如何通过滑动窗口和超时重传来确保数据传输的可靠性，同时介绍了流量控制和拥塞控制的基本原理及其在实际网络通信中的应用。 ... [详细]

蜡笔小新 2024-11-21 18:52:07
session
Maven + Spring + MyBatis + MySQL 环境搭建与实例解析

本文详细介绍如何使用MySQL数据库进行环境搭建，包括创建数据库表并插入示例数据。随后，逐步指导如何配置Maven项目，整合Spring框架与MyBatis，实现高效的数据访问。 ... [详细]

蜡笔小新 2024-11-21 18:39:23
python
Python 开发环境最佳实践：Anaconda + Jupyter Notebook 快速上手指南

对于初学者而言，搭建一个高效稳定的 Python 开发环境是入门的关键一步。本文将详细介绍如何利用 Anaconda 和 Jupyter Notebook 来构建一个既易于管理又功能强大的开发环境。 ... [详细]

蜡笔小新 2024-11-21 18:30:23
python
使用TabActivity实现Android顶部选项卡功能

本文介绍如何通过继承TabActivity来创建Android应用中的顶部选项卡。通过简单的步骤，您可以轻松地添加多个选项卡，并实现基本的界面切换功能。 ... [详细]

蜡笔小新 2024-11-21 17:47:42

拍友2502906483

这个家伙很懒，什么也没留下！

Tags | 热门标签

RankList | 热门文章