作者：手机用户2502852661 | 来源：互联网 | 2023-07-18 20:51
人工神经网络
- 人工神经网络简介
- 代码
- 神经网络的缺点
- 程序优化
- BP算法
- 补充
人工神经网络简介
人工神经网络(Artificial Neural Network, ANN)是指一系列受生物学和神经学启发的数学模型. 在人工智能领域, 人工神经网络也常常简称为神经网络(Neural Network, NN)或神经模型(Neural Model). 一个简单的多层前馈神经网络如下图.
代码
构造一个神经网络类, 首先需要将一些变量进行初始化，其中各个层的权重矩阵以及偏置项分别存储在字典中, 键代表层数.
from scipy.special import expit
import numpy as np
class ANN(object):
def __init__(self, innum, outnum, lr, *hide_tuple):
self.innum = innum
self.outnum = outnum
self.lr = lr
self.layernum = len(hide_tuple) + 1
self.Weight = {}
self.Bias = {}
self.Weight[1] = np.random.normal(0.0, pow(self.innum, -0.5), (hide_tuple[0], self.innum))
for i in range(1, self.layernum):
self.Bias[i] = np.random.randn(hide_tuple[i-1]).reshape(hide_tuple[i-1], 1)
if i>=2:
self.Weight[i] = np.random.normal(0.0, pow(hide_tuple[i-1], -0.5), (hide_tuple[i-1], hide_tuple[i-2]))
self.Weight[self.layernum] = np.random.normal(0.0, pow(hide_tuple[-1], -0.5), (self.outnum, hide_tuple[-1]))
self.Bias[self.layernum] = np.random.randn(self.outnum).reshape(self.outnum, 1)
self.ActiveFunction = lambda x: expit(x)
接下来通过BP算法反向求解误差，进而不断更新权重和偏置项, 其中将所有层的输入和输出分别存入相应的字典中, 键代表相应的层数.
def BPFit(self, input_list, target_list):
Input0 = np.array(input_list, ndmin=2).T
TargetValue = np.array(target_list, ndmin=2).T
Input = {}
Output = {}
Output[0] = Input0
for i in range(1, self.layernum+1):
Input[i] = np.dot(self.Weight[i], Output[i-1])
Output[i] = self.ActiveFunction(Input[i] + self.Bias[i])
Error={}
Error[self.layernum] = Output[self.layernum] * (1 - Output[self.layernum]) * (-(TargetValue - Output[self.layernum]))
self.Weight[self.layernum] -= self.lr * Error[self.layernum] * Output[self.layernum-1].T
self.Bias[self.layernum] -= self.lr * Error[self.layernum]
for i in range(self.layernum-1, 0, -1):
Error[i] = Output[i] * (1 - Output[i]) * np.dot(self.Weight[i+1].T, Error[i+1])
self.Weight[i] -= self.lr * Error[i] * Output[i-1].T
self.Bias[i] -= self.lr * Error[i]
接着再添加一个预测函数, 它是用来实现神经网络预测功能的成员函数.
def predict(self, input_list):
Input0 = np.array(input_list, ndmin=2).T
Input = {}
Output = {}
Output[0] = Input0
for i in range(1, self.layernum + 1):
Input[i] = np.dot(self.Weight[i], Output[i - 1])
Output[i] = self.ActiveFunction(Input[i] + self.Bias[i])
return Output[self.layernum]
最后来测试一下程序是否可以正确运行. 在测试中, 小编任选一个4维的输入向量, 1维的输出向量, 中间添加了四个隐藏层.
if __name__ == '__main__':
"""
测试样例
"""
inode = 4
hnode1 = 4
hnode2 = 5
hnode3 = 10
hnode4 = 5
onodenum = 1
learningrate = 0.3
ann = ANN(inode, onodenum, learningrate, hnode1, hnode2, hnode3, hnode4)
TrainValue = [1, 3, 2, 4]
TargetValue = [0]
ann.BPFit(TrainValue, TargetValue)
TestValue = [2, 4, 2, 4]
predict = ann.predict(TestValue)
print(predict)
预测结果为:
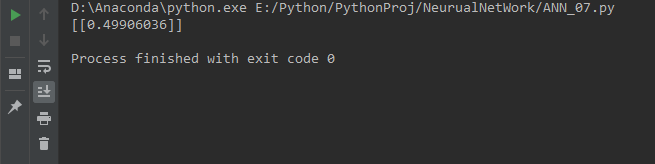这样就实现了简易版神经网络的搭建.
神经网络的缺点
- 可解释性差
神经网络相当于一个黑箱模型, 不知道能产生什么结果, 也不知道为什么产生这种结果. 但是决策树可以遵循一定的逻辑, 如果出问题也能想出来原因, 比如银行就不会用神经网络预测一个人的信誉.
- 耗时耗力
训练大型的神经网络需要花费大量的时间以及需要大量的内存来对神经网络进行训练
- 样本量大
为了得到一个预测能力强的神经网络, 前提是需要大量的样本
- 信息丢失
因为在训练神经网络时, 需要把样本都转换成数值型, 在转化的过程中就会用信息丢失.
程序优化
虽然实现了简易版的神经网络, 并且可以任意设置层数以及神经元的个数, 但是为了提高预测的准确率和运行速度, 还可以从许多方面对该程序进行优化. 比如:
- 初始权重矩阵以及偏置项
- 样本量
- 优化器的种类
- 优化器的学习率
- 神经网络的层数
- 神经元的个数
- 激活函数
- 损失函数
- 训练次数
BP算法
本文中的神经网络是基于BP算法来搭建的. 在本文结尾引用的书籍中, 对于该算法有详细的介绍, 在这里小编就不再详细介绍该算法了, 感兴趣的小伙伴们可以了解一下哈~
补充
这是小编的第一篇博文, 也是小编初入互联网大家庭的一个标志. 因为本篇文章主要靠小编自己的理解去写的, 所以可能存在一些不是很恰当的词语, 还请大家多多包容与理解. 最后立个flag, 小编会继续加油, 希望可以早日甩掉技术小白的称号！！！(ps: Python源码已经上传到小编的github)
[1]: 邱锡鹏. 神经网络与深度学习.
京公网安备 11010802041100号