Part VIII 因子分析 主成分分析 独立成分分析

在上个部分介绍了EM算法&＃xff0c;在此部分因子分析中&＃xff0c;我们会再次应用到。

因子分析、主成分分析和独立成分分析都作为对于数据维度进行处理的手段&＃xff0c;对于我们理解数据、更好的表示数据都起到或多或少的作用&＃xff0c;因此将三者放在一起进行叙述。

目录

Part VIII 因子分析 主成分分析 独立成分分析

1 因子分析&＃xff08;Factor Analysis&＃xff0c;FA&＃xff09;

1.1 背景

1.2 思想与推导

2 主成分分析&＃xff08;Principal Components Analysis&＃xff0c;PCA&＃xff09;

3 独立成分分析&＃xff08;Independent Components Analysis,ICA&＃xff09;

4 小结

1 因子分析&＃xff08;Factor Analysis&＃xff0c;FA&＃xff09;

首先介绍因子分析&＃xff08;FA&＃xff09;的提出背景&＃xff0c;接着给出算法的思想&＃xff0c;最后结合EM算法给出其参数的推导。

1.1 背景

之前介绍的各种算法&＃xff0c;我们都有着一个不容忽视假设&＃xff1a;样本的数量m足够充足&＃xff0c;这样就使得通过训练&＃xff08;迭代&＃xff09;&＃xff0c;能够求解出参数从而构造出模型。但是现实有时候是残酷的&＃xff0c;有时候会存在样本的数量匮乏的情况&＃xff08;m<

但是在当前样本数量m<

这是一个很强的限制&＃xff0c;因为这种限制认为各个参数之间是独立的&＃xff0c;实际情况下是不可取的。在协方差阵为对角阵的基础之上&＃xff0c;还可以进一步限制&＃xff0c;即协方差阵中的对角元素取值相同。这两种强限制条件大多数情况下感觉都不太适用。

在没有限制条件即原有条件下&＃xff0c;需满足

&＃xff08;2&＃xff09;原始数据空间x为n&＃xff08;图中n&＃61;2&＃xff09;维。可以将低维空间变量通过变换矩阵

&＃xff08;3&＃xff09;每个样本加上n维偏移向量

&＃xff08;4&＃xff09;每个样本加上n维高斯扰动ε~N(0,ψ)从而得到高维向量x

由上&＃xff0c;可将因子分析模型总结如下&＃xff1a;

从高维向量x可由潜在的低维高斯型向量z线性表示出发&＃xff0c;存在着以下假设&＃xff0c;并且在下列分布中隐变量z与随机高斯噪声

第一行表示潜在型高斯变量分布。

第二行表示随机高斯噪声的影响。

第三行表示x由z线性表示形式。

结合上述定义&＃xff0c;不难得到&＃xff08;确保明白这点&＃xff09;

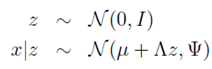
接下来&＃xff0c;对于x和z的联合分布建模。由于p(x,z)&＃61;p(x|z)*p(z)&＃xff0c;两个高斯型密度函数的乘积仍然为高斯型&＃xff0c;因此将x&＃xff0c;z联合分布建模为高斯型如下&＃xff1a;

之所以在左端写成矩阵形式&＃xff0c;仅仅是为了接下来的表述方便。那么参数

那么就有&＃xff1a;

到这里就很清晰了。还是老套路&＃xff0c;接下来利用最大似然法求解参数从而得到x&＃xff0c;z的联合分布。此时参数为

能够直接求偏导解出上述参数算你厉害。

此方程比较复杂&＃xff0c;很难直接解出&＃xff0c;因此就需要利用上一讲介绍EM算法进行求解了。在上一讲最后利用高斯混合模型对于EM算法的流程已经进行过介绍了。对于高斯混合模型而言&＃xff0c;隐变量z为离散型&＃xff0c;而在因子分析中隐变量z则为连续性&＃xff1b;其实就是将求和改为积分即可。下面给出EM算法的解参数步骤&＃xff1a;

&＃xff08;1&＃xff09;E-step&＃xff1a;在E-step中&＃xff0c;我们需要根据参数计算得到后验概率

那么可得以下结论&＃xff1a;

因此&＃xff0c;根据此结论和前文的推导&＃xff0c;可得后验分布

以上&＃xff0c;E-step顺利走通。

&＃xff08;2&＃xff09;M-step&＃xff1a;在M-step&＃xff0c;我们要最大化&＃xff1a;

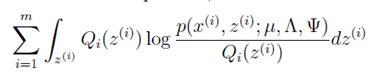
简化此式得到&＃xff1a;

然后分别对于参数

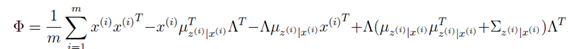
在每次迭代中&＃xff0c;更新参数的值直到收敛从而得到最终参数的结果。

由此&＃xff0c;求解出三个参数&＃xff0c;原有的n维&＃xff08;高维&＃xff09;空间样本x便可由k维&＃xff08;低维&＃xff09;空间隐变量z线性表示了。

2 主成分分析&＃xff08;Principal Components Analysis&＃xff0c;PCA&＃xff09;

主成分分析&＃xff08;PCA&＃xff09;作为另外一种数据降维的手段得到了广泛的应用。

主成分分析的思想在于&＃xff0c;在数据维度&＃xff08;n维&＃xff09;较大时&＃xff0c;各个维度之间或多或少都会存在着相关性&＃xff0c;而实际上我们并不需要全部使用维度进行处理&＃xff0c;因为或许选取数据的某k维就代表了很大部分的n维特征。PCA的过程就是提取这k维的过程。

解释PCA可以从将近10种思路出发&＃xff0c;这里选取比较好理解的最大方差的思路出发进行解释。

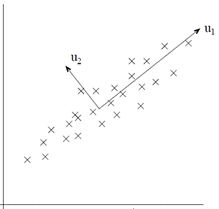
以2维数据压缩为1维数据为例&＃xff0c;PCA要做的找到一个新的维度&＃xff0c;是数据在新维度上的方差最大&＃xff08;即投影长度最长&＃xff0c;如u1的方向所示&＃xff09;。因为根据信息论的观点&＃xff0c;数据所包含的方差越大&＃xff0c;那么数据所包含的信息量越大。如果新的投影方向u1能够包含原有数据的大部分信息&＃xff08;假设85%以上&＃xff09;&＃xff0c;那么可以认为在保证了数据信息的精度上进行了压缩。

再举一个例子&＃xff0c;假设原有5个2维样本如下图所示。

分别将原始数据按照如图所示的两个方向进行投影&＃xff0c;得到左图与右图。

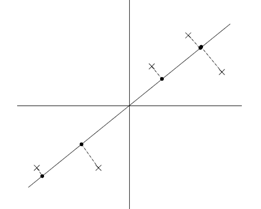
这就很清晰了&＃xff0c;左图的数据明显比右图更能保留原始的数据信息。

那么包含了数据最多的新的投影方向是什么方向呢&＃xff1f;听上去是一个解最值的问题&＃xff0c;实际上也正是这样。

首先对于数据预处理。预处理的目的在于使各个维度的数据在接下来的处理中拥有着相同的尺度。预处理步骤如下。

&＃xff08;1&＃xff09;计算    

因此&＃xff0c;优化问题即为在|u|&＃61;1的条件下&＃xff0c;使下式最大化

利用拉格朗日乘数法即可解决&＃xff0c;这里设

对u求偏导&＃xff0c;并另偏导等于0&＃xff0c;得

又因为

从而推出&＃xff1a;

接下来又到了求参环节了&＃xff0c;这里我们的参数是W&＃xff0c;同样利用最大似然法进行参数的求解。写出最大似然方程&＃xff1a;

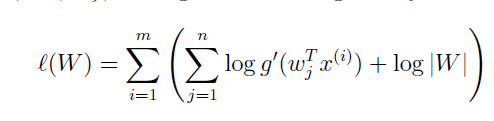
对W求偏导&＃xff0c;可得每次迭代的更新公式为&＃xff1a;

为了表述方便&＃xff0c;可将解得的W写成如下形式&＃xff1a;

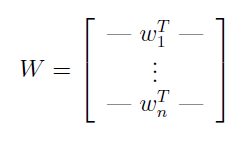
根据W&＃xff0c;那么原有数据中的每个信号的来源即可分离开了。即每个。由此ICA从原有混合数据中将来源于不同信号源的数据进行分离的任务便完成了。

4 小结

或许有人会疑惑同样是作为数据降维的手段&＃xff0c;好像最后的形式也差不多&＃xff0c;因子分析&＃xff08;FA&＃xff09;和主成分分析&＃xff08;PCA&＃xff09;有什么区别呢&＃xff1f;看完二者的推导&＃xff0c;谈谈我的看法。

首先&＃xff0c;差别还是挺明显的&＃xff0c;二者的思想出发点就不同。FA是想从众多特征中找出一些共性&＃xff08;即隐变量z&＃xff09;&＃xff0c;利用共性对于原有数据进行表达&＃xff1b;而PCA则是从众多特征中找出一些具有代表性的特征对于原有特征进行表达。

其次&＃xff0c;二者的着重点也不一致。FA着重于各个变量间的协方差&＃xff1b;而PCA则着重于总体的方差。

再者&＃xff0c;FA相比较而言做了一些假设&＃xff0c;较为受到限制&＃xff1b;而PCA则无需假设&＃xff0c;应用更广。

最后&＃xff0c;PCA的实际应用范围是大于FA的。PCA在许多方面都发挥着不小的作用。

独立成分分析&＃xff08;ICA&＃xff09;的目的在于从多个信号混杂的数据中&＃xff0c;解算出每个信号原有的数据。为此ICA做了一些假设&＃xff0c;包括确定信号的分布函数。在ICA中应该留意&＃xff0c;高斯分布的数据并不能直接应用ICA做分解。