1 Recipe of Deep Learning

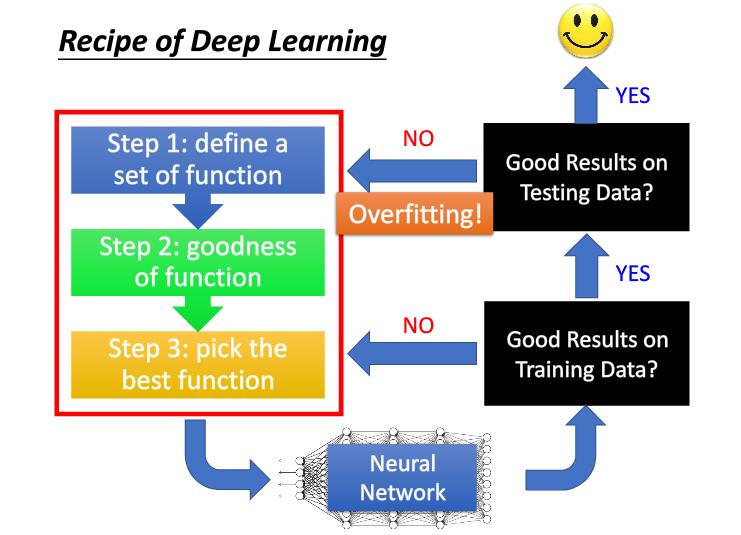
我们在搭建与训练神经网络的时候最好使用上图步骤&＃xff1a;

1. 快速搭建好神经网络模型
2. 看训练集上有没有好的结果&＃xff0c;如果有那么执行3&＃xff0c;如果没有高偏差执行4
3. 看测试集上有没有好的结果&＃xff0c;如果有执行6&＃xff0c;如果没有高方差执行5
4. 选择更好的模型&＃xff0c;如增加网络的深度&＃xff0c;增加迭代次数&＃xff0c;改变学习率等
5. 因为过拟合&＃xff0c;所示使用如regularization&＃xff0c;EarlyStopping&＃xff0c;Dropout&＃xff0c;增大数据集等方法
6. 训练完成

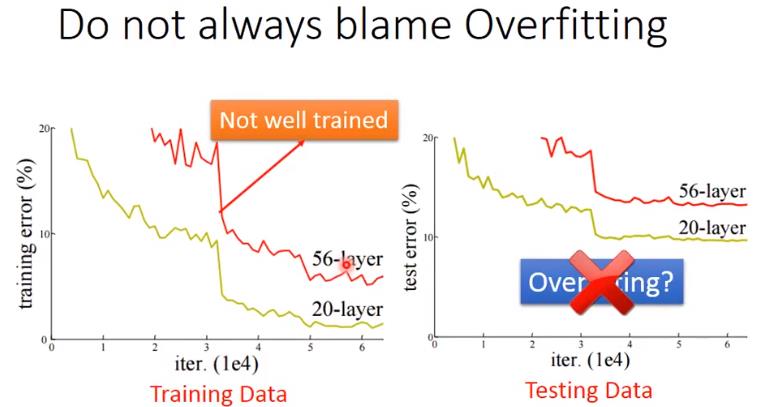
因此我们在训练集上测试不理想的时候&＃xff0c;不能首先就 认为是因为overfitting&＃xff0c;也有可能是训练集上的训练结果就不好。如下图&＃xff0c;56层的神经网络在测试集上的准确率没有20层好&＃xff0c;但我们不能说是因此overfitting的原因&＃xff0c;也有可能是训练集上56层的没有训练好。

2 Good Results on Training Data?

2.1 New activation function

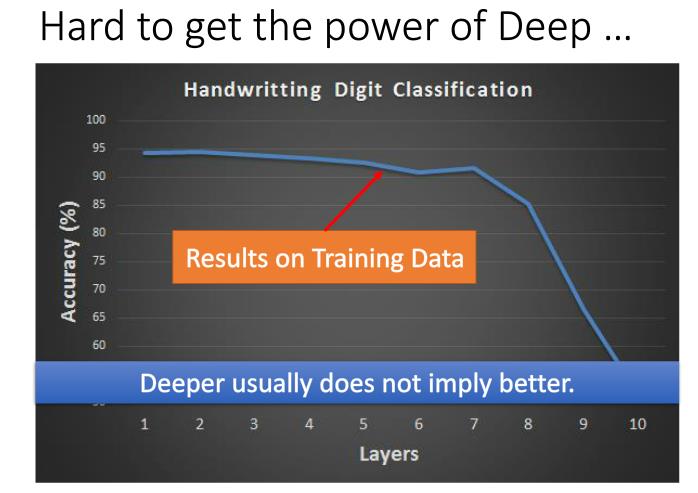
之前激活函数一般是sigmoid函数&＃xff0c;对于训练集&＃xff0c;神经网络更深的深度不代表有更好的结果&＃xff0c;如上图&＃xff0c;当神经网络深度为7层的时候&＃xff0c;准确率就开始逐渐下降。

梯度消失问题

如上图&＃xff0c;靠近input的参数对最后loss functiong的微分值比较小&＃xff0c;但靠近output的参数的微分值比较大。所以靠近input的参数跟新很慢&＃xff0c;而靠近output的参数跟新很快&＃xff0c;最终靠近input的参数几乎还是随机的&＃xff0c;没有学到东西。

对于神经网络&＃xff0c;梯度表示当前参数的变化对最终loss的影响程度&＃xff0c;因为使用sigmoid函数&＃xff0c;会将输出值压缩到0-1之间&＃xff0c;因此靠近input的参数变化随着网络深度的加深&＃xff0c;对output的影响越来越小&＃xff0c;因此梯度值就越来越小。学习到的东西就越来越少。

为了解决这个问题&＃xff0c;早期的做法是RBM&＃xff0c;即先训练第一个layer&＃xff0c;在训练第二个&＃xff0c;在训练第三个。这样在反向传播的时候&＃xff0c;第一层没有更新慢也没关系&＃xff0c;因为已经更新好了。

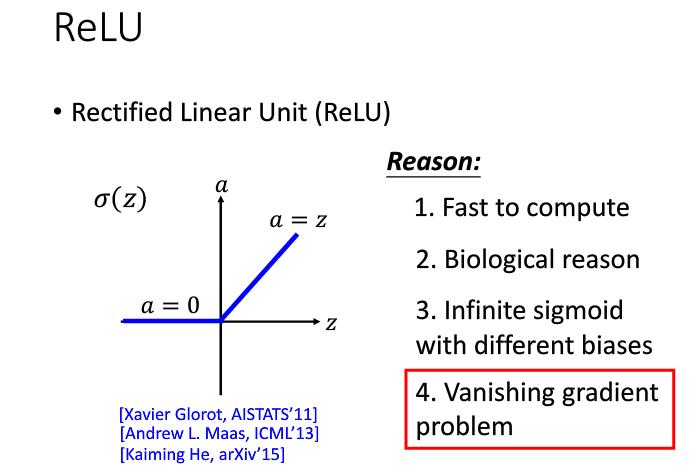
现在的做法是改变激活函数&＃xff0c;使用ReLU&＃xff08;Rectified Linear Unit&＃xff09;激活函数,它可以解决梯度消失的问题 。因为把等于0的神经元拿掉&＃xff0c;ReLU的神经网络就成了一个瘦长的线性网络了&＃xff0c;就不有梯度值非常小的问题了。

使用ReLU神经网络还是非线性的&＃xff0c;因为每次计算神经元的值作用域是不一样的&＃xff08;小于0跟大于0&＃xff09;&＃xff0c;因此神经网络还是非线性的&＃xff0c;如果作用域也一样那就是线性的了。

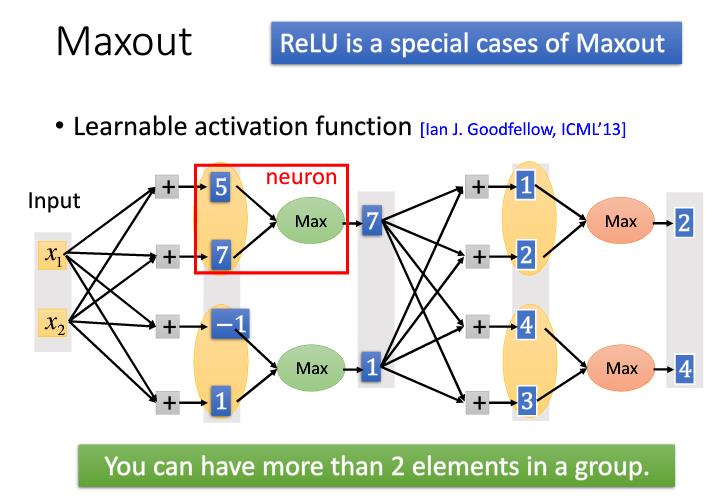
除了ReLU还有一些其他的激活函数如下图&＃xff0c;其中Maxout跟MaxPooling其实是一样的运算。

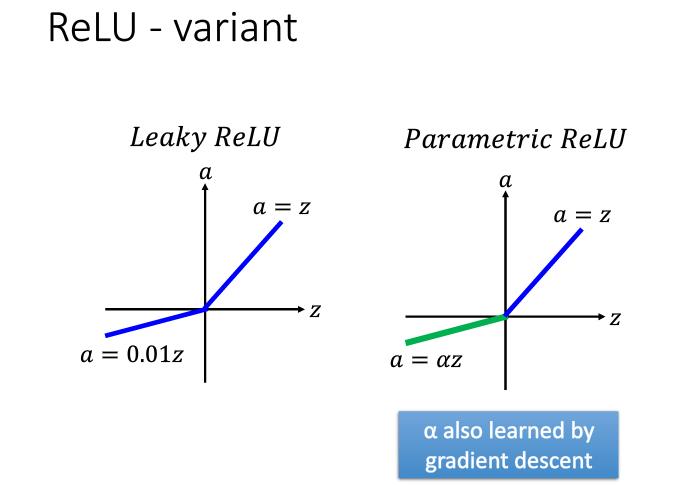
2.2 Adaptive Learning Rate

2.2.1 AdaGrad

由公式可以看出&＃xff0c;若平时梯度值较小&＃xff0c;即在这个维度上比较平缓&＃xff0c;则让它的学习率便大一些&＃xff0c;因为历史的梯度平方做分母。同理若平时梯较大&＃xff0c;即在这个维度上比较陡峭&＃xff0c;则让它的学习率便小一些。下面链接也有解释

Deep Learning 最优化方法之AdaGrad - 忆臻的文章 - 知乎
https://zhuanlan.zhihu.com/p/29920135

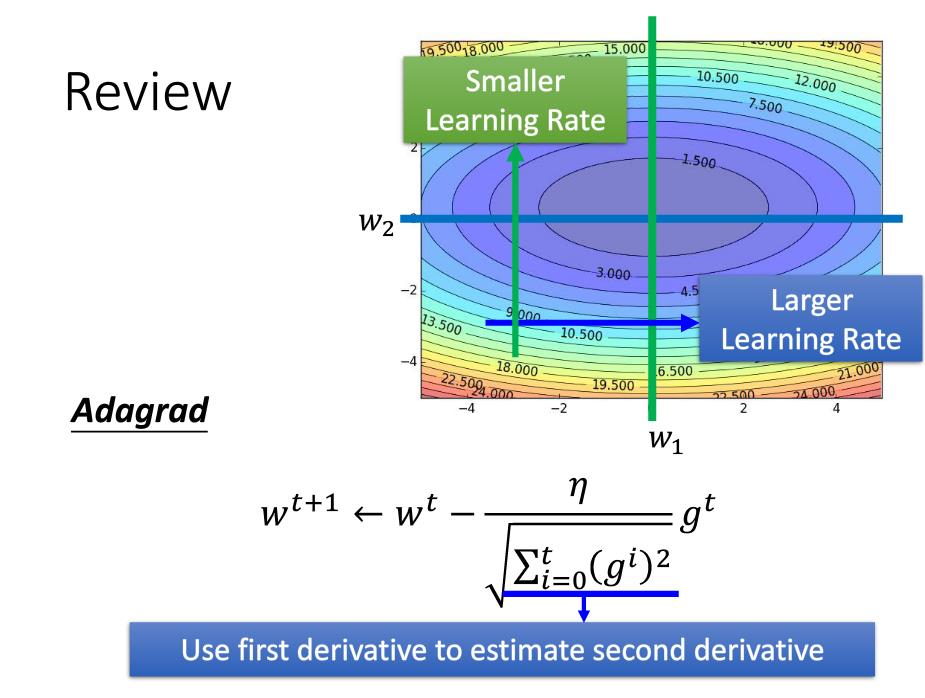但由于历史梯度平方和是递增的&＃xff0c;因此会使得学习率衰减到0&＃xff0c;可能是训练提前结束。

2.2.2 RMSprop

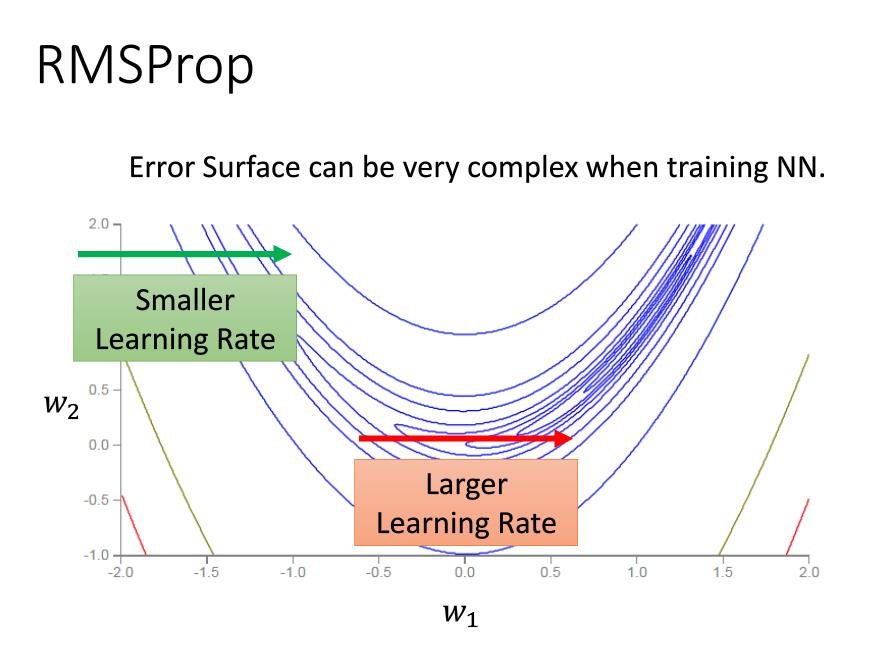
在实际问题中&＃xff0c;我们的损失值的等高线图不会是很规则的形状&＃xff0c;如下图&＃xff0c;因此有了了RMSProp&＃xff0c;对比Adagrad,使用的为历史梯度平方和&＃xff0c;Rmsprop采用了指数加权平均的方式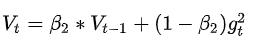即二阶动量的&＃xff0c;当前的梯度值跟历史梯度值与当前梯度值有关&＃xff0c;历史梯度值跟\(\beta_2\)有关.就避免了二阶动量持续积累导致训练提前结束。

2.2.3 Momentum

这里有个问题是&＃xff0c;我们不需要太担心局部最优解的情况&＃xff0c;因为这种情况是比较少了&＃xff0c;局部最优解要求每个维度的梯度值都等于0 &＃xff0c;但实际上我们有很多的维度。

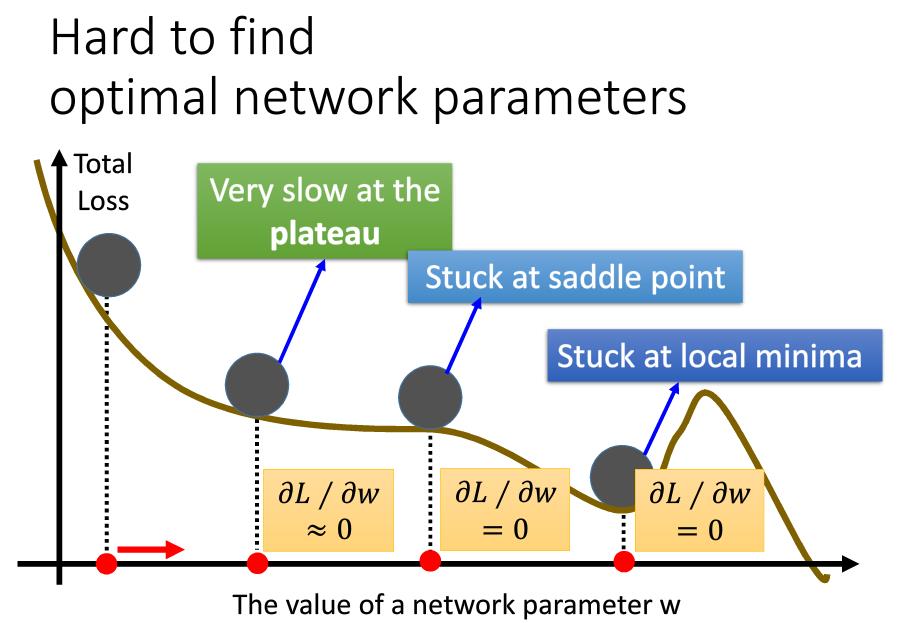
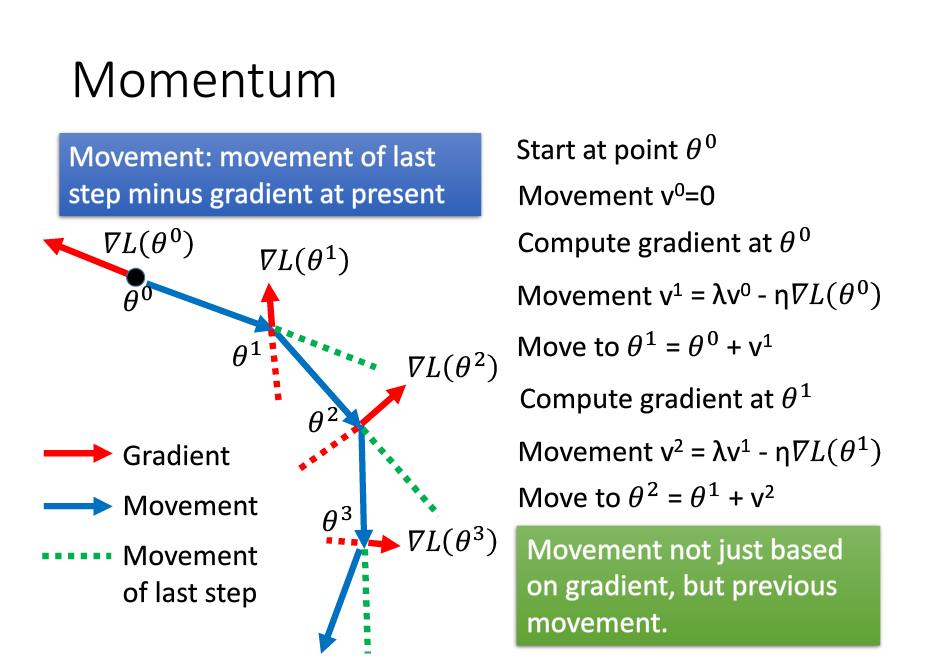
动量梯度下降可是使我们参考历史梯度值。即是我们在求最优解的时候有了惯性。Momentum的公式为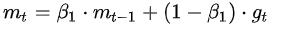&＃xff0c;它约等于最近\(1/(1-\beta_1)\)个时刻的梯度向量和平均值。

2.2.4 Adam

RMSProp&＃43;Momentum形成Adam计算方法如下

3 Good Results on Testing Data?

训练结果好&＃xff0c;而测试集结果不好&＃xff0c;是因为发生了过拟合&＃xff0c;有Early Stopping 、Regularization与Dropout等方法可以使用&＃xff0c;其中Early Stopping 跟 Regularization是一个传统的方法&＃xff0c;机器学习只要发生过拟合基本都能使用&＃xff0c;而Dropout一般适用于神经网络中。

3.1 Early Stoping

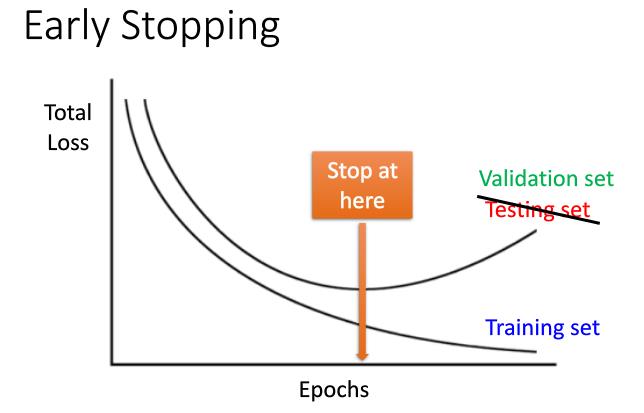
如下图&＃xff0c;因为过拟合的原因&＃xff0c;测试集或验证集的精度会随着迭代次数的增加而降低&＃xff0c;因此我们可以提早结束循环。

3.2 Regularization

正则化一般用L2正则化&＃xff0c;或者L1正则化&＃xff0c;L2用的最多。

3.2.1 L2正则化

下图为L2的正则化公式&＃xff0c;即在原来的损失函数上加上\(\frac 1 2\lambda\)乘每个参数的平方和。

意义是这样的&＃xff0c;如下图对加了L2正则化项的损失函数求导&＃xff0c;结果为\((1-\eta\lambda)w^t-\eta\frac {\partial L} {\partial w}\)其中\(\eta,\lambda\)都大于0&＃xff0c;因此\((1-\eta\lambda)\)总会小于1所以\(w^t\)总会越来越接近0。这称为权重衰减

3.2.2 L1 正则化

下图为L1正则化&＃xff0c;即在原来的损失函数上加上\(\frac 1 2\lambda\)乘每个参数的绝对值。

L1正则化的意义如下图&＃xff0c;对加了L1正则化的损失函数求导得到\(w^t-\eta \frac{\partial L}{\partial w}-\eta\lambda sgn(w^t)\),当我们的\(w^t\)为正值的时候&＃xff0c;\(sgn(w^t)\)为1&＃xff0c;因此会减去一个正值\(\eta\lambda\),\(w^t\)的值会变小&＃xff0c;接近0&＃xff0c;当\(w^t\)为负值的时候&＃xff0c;\(sgn(w^t)\)为\(-1\)&＃xff0c;因此会减去一个负,\(w^t\)的值\(\eta\lambda\)会变大&＃xff0c;接近0&＃xff0c;因此L1正则化的作用也是使参数越来越接近0.

跟L2正则化\((1-\eta\lambda)w^t-\eta \frac{\partial L}{\partial w}\) 梯度更新相比&＃xff0c;L1每次更新减去一个固定的值&＃xff0c;而L2正则化是乘以一个小于1的数。因此L2正则化会使参数都很接近0&＃xff0c;但不等于0。L1因为减去固定值&＃xff0c;所以参数值会有很多等于0的值。同时若参数初始化为一个很大的值&＃xff0c;L2正则化会使参数值下降的非常快。

3.2.3 Dropout

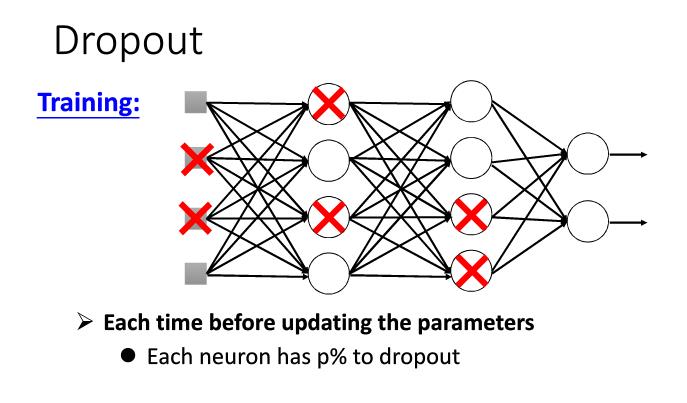
在训练的时候&＃xff0c;每个epochs每个节点都会有%p的概率被删掉。删掉节点后的神经网络如下。

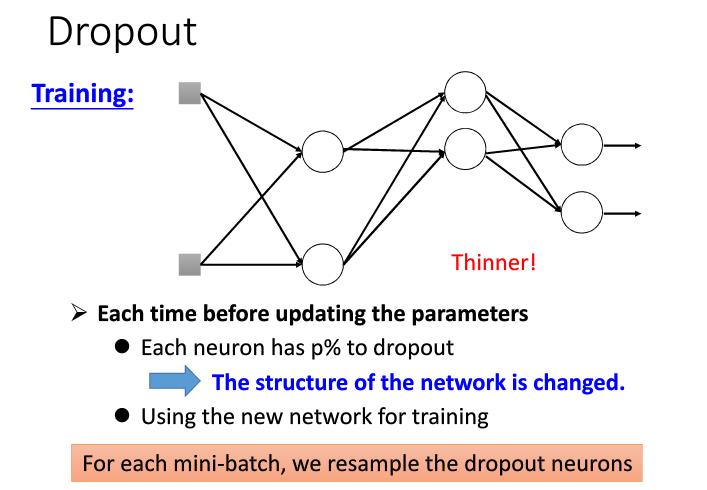
在测试的时候&＃xff0c;每个参数都应该乘1-%p​,因为在测试的时候&＃xff0c;如果我们想得到跟训练时候接近的神经元的值&＃xff0c;我们应该将参数缩小一点。如下图。

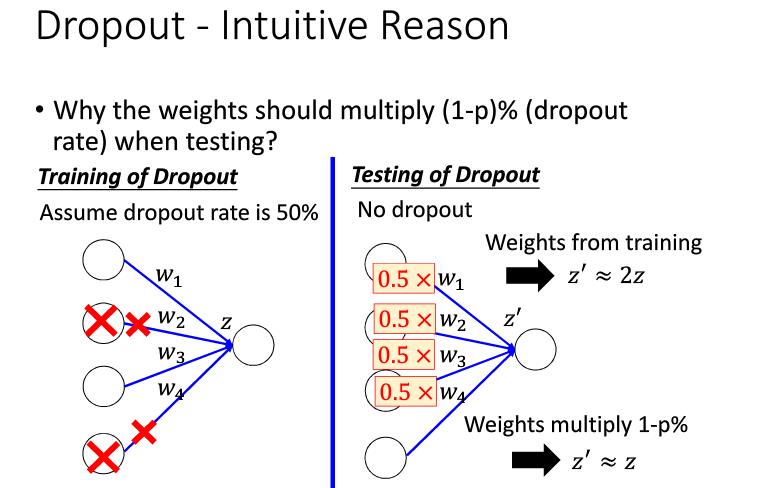
dropout为什么会有用呢&＃xff0c;是因为dropout实际上使一种ensemble&＃xff08;多个模型取平均结果&＃xff09;。即相当于训练了多个模型&＃xff0c;而这些模型的参数使共享的。达到了ensemble的效果。

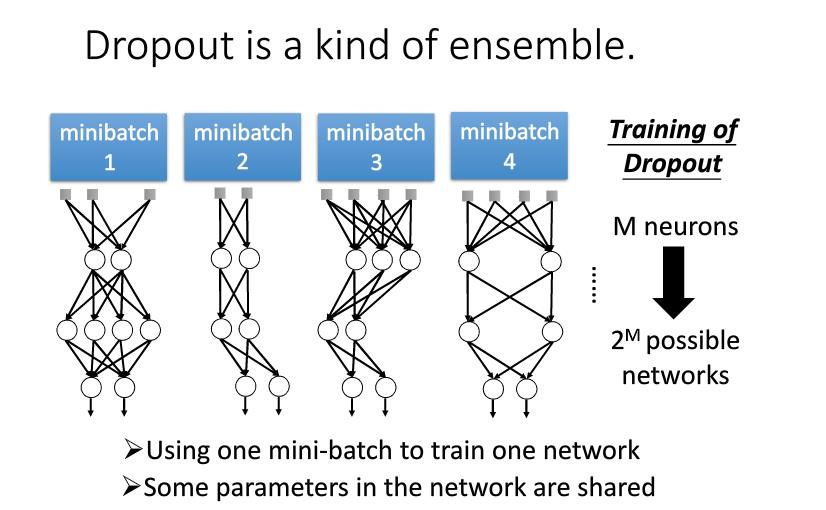
4 Kears提示

如果我们在训练模型的时候&＃xff0c;测试集的损失值跟精度不好&＃xff0c;可能有下面几个原因&＃xff1a;

1. loss function设的不好。如做分类的时候&＃xff0c;mean square error损失函数不合适
2. batch_size也会对结果有影响
3. 激活函数的原因&＃xff1a;sigmoid在深层神经网络结果特别不好&＃xff0c;最好用ReLU
4. 个别时候是否normalization也会有影响
5. 优化器的影响&＃xff0c;如使用adagrad、adam、sgd有不同结果
6. 过拟合&＃xff0c;可以加上Dropout