系统集成资质培训 - 难题分析 - 资源约束经典题型

作者&＃xff1a;刘毅 lypmpok&＃64;163.com 转载注明出处

 

本题第一种解题方法参考&＃xff1a;http://pmpok.blog.51cto.com/44246/975635

●某企业需要采用甲、乙、丙三种原材料生产Ⅰ、Ⅱ两种产品。生产两种产品所需原材料数量、单位产品可获得利润以及企业现有原材料数如表所示&＃xff1a;

 

产品&＃xff08;吨&＃xff09;

现有原材料&＃xff08;吨&＃xff09;

Ⅰ

Ⅱ

资源

甲

1

1

4

乙

4

3

12

丙

1

3

6

单位利润&＃xff08;万元/吨&＃xff09;

9

12

 

则公司可以获得的最大利润是 &＃xff08;66&＃xff09; 万元。取得最大利润时&＃xff0c;原材料 &＃xff08;67&＃xff09; 尚有剩余。

&＃xff08;66&＃xff09; A&＃xff0e;21                 B&＃xff0e;34               C&＃xff0e;39               D&＃xff0e;48

&＃xff08;67&＃xff09; A&＃xff0e;甲                 B&＃xff0e;乙               C&＃xff0e;丙               D&＃xff0e;乙和丙

 

试题分析&＃xff1a;

本题属于线性规划问题。

设生产Ⅰ、Ⅱ两种产品分别为x吨、y吨&＃xff0c;公司获利z&＃61;9x&＃43;12y万元&＃xff0c;依据题意有&＃xff1a;

 

 

约束条件&＃xff1a; x&＃43;y<&＃61;4
4x&＃43;3y<&＃61;12
x&＃43;3y<&＃61;6
目标函数&＃xff1a;Max z&＃61;9x&＃43;12y

我们使用运筹学中的图解法解决这类问题&＃xff1a;

&＃xff08;1&＃xff09;由全部约束条件做图得到可行域

考虑约束条件1.1&＃xff0c;若取等号的x&＃43;y&＃61;4&＃xff0c;做直线&＃xff0c;将坐标系划分为两个部分。同理做4x&＃43;3y&＃61;12、x&＃43;3y&＃61;6&＃xff0c;x&＃61;0&＃xff0c;y&＃61;0的直线。

全部约束条件相应部分&＃xff0c;交集即为线性规划问题的可行域。具体如图1所示。

 

 

 

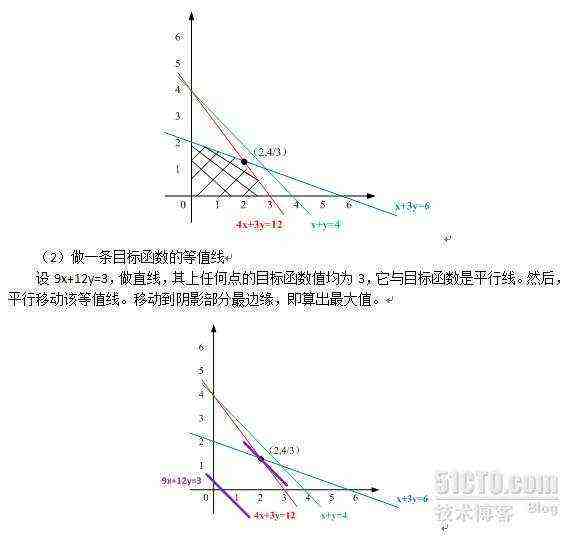
本题&＃xff0c;顶点&＃xff08;2&＃xff0c;4/3&＃xff09;为最优点&＃xff0c;即产品Ⅰ、Ⅱ分别为2吨、4/3吨。

代入Max z&＃61;9x&＃43;12y得到MAX

本题第2问。

甲原料需要花费2&＃43;4/3吨&＃xff0c;乙原料需要花费2*4&＃43;4/3*3&＃61;12吨&＃xff0c;丙原料需要花费4&＃43;4/3*3&＃61;8吨&＃xff0c;这里只有甲还有剩余。

参考答案

&＃xff08;66&＃xff09;B  &＃xff08;67&＃xff09;A