文本表示模型(1)：主题模型LSA、pLSA、LDA

文本表示模型

文本表示模型可分为以下几种：

• 基于one-hot, tf-idf, textrank等的bag-of-words；
• 基于计数的，主题模型，如LSA, pLSA, LDA
• 基于预测的，静态词嵌入，如Word2Vec, FastText, Glove
• 基于大规模预训练的，动态词嵌入，如BERT, ELMo, GPT, T5

本文讲解第二种“主题模型”。

主题模型

主题模型的目标是在大量的文档中自动发现隐含的主题信息

LSA

LSA（Latent Semantic Analysis，潜在语义分析）

首先构建doc-word共现矩阵，矩阵元素为词的tf-idf值（常见词不一定和主题相关，所以tf-idf比词频适用）。

为了找到潜在的语义（主题），LSA利用奇异值分解SVD，把高维的doc-word共现矩阵映射（降维）到低维的潜在语义空间，得到映射后的文档向量和词向量，并且具有相似主题分布的文档（或词）向量接近。

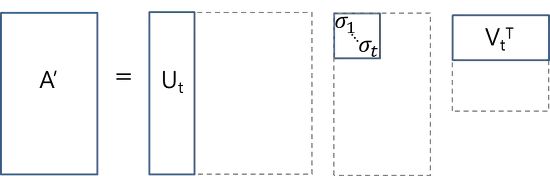
如上图所示，SVD将doc-word共现矩阵 A 分解为U、S、V三个矩阵的乘积

• U∈R(m⨉t)U∈ℝ^{(m⨉t)}U∈R(m⨉t)是潜在语义空间中的doc-topic矩阵，行表示按t个主题表达的文档向量；
• VT∈R(n⨉t)V^T∈ℝ^{(n⨉t)}VT∈R(n⨉t)是潜在语义空间中的topic-word矩阵，列代表按t个主题表达的词向量；
• U和V是列向量彼此正交的正交矩阵；
• S 是一个对角矩阵，奇异值在对角线上降序排列，可视为该维度的重要性；
• t 是一个超参数，根据待查找的主题数量进行选择和调整。

有了LSA文档向量和词向量，可计算不同文档的相似度、不同词的相似度、词（或query）与文档的相似度

缺点：

• 缺乏严谨的数理统计基础
• SVD分解慢。如果矩阵大小是N，SVD的计算复杂度达到O(N^3)，不过可以使用Truncated SVD等更快的方法。

pLSA

pLSA（probabilistic Latent Semantic Analysis，概率潜在语义分析）

将LSA的思想带入到概率统计模型中，不再使用SVD，是一种生成式概率图模型（可以写成若干条件概率连乘），用EM算法学习模型参数。

如上图，给定文档 d，主题 z 以 P(z|d) 的概率出现在该文档中；给定主题 z，单词 w 以 P(w|z) 的概率从主题 z 中被选取。在这个模型中，d 和 w 是已经观测到的变量，而 z 是未知的变量(代表潜在的主题)。其中 P(z|d) 和 P(w|z) 是pLSA模型需要求解的参数。

注：pLSA 模型和 LSA 模型之间存在一个直接的平行对应关系：

缺点：

• 无法得知新文档的 P(d)
• pLSA 的参数量随文档数量线性增长，容易过拟合

LDA

LDA（Latent Drichlet Allocation，潜在狄利克雷分配）

LDA 是 pLSA 的贝叶斯版本，在 pLSA 的基础上，引入了参数的狄利克雷先验分布。

• pLSA采用的是频率学派思想：把 P(z|d) 和 P(w|z) 这两个待估计的参数，看作固定的未知常数，可以求解出来（通过样本计算最大似然估计）。
• LDA采用的是贝叶斯学派思想：把 P(z|d) 和 P(w|z) 这两个待估计的参数，看作服从一定分布的随机变量（这个分布符合狄利克雷先验概率分布），可通过样本修正先验分布，获得后验分布；
• 狄利克雷是一种「分布的分布」。它回答了：「给定某种分布，我看到的实际概率分布可能是什么样子？」

注：pLSA 相当于把 LDA 的先验分布转为均匀分布，然后对参数求最大后验估计(在先验是均匀分布的前提下，这也等价于求参数的最大似然估计)，而这也正反映出了一个较为合理的先验对于建模是非常重要的。

P(w,Z,B,Θ∣α,η)=∏t=1Tp(Θt∣α)∏i=1Kp(βk∣η)(∏n=1NP(wt,n∣zt,n,βk)P(zt,n∣Θt))P(w,Z,\Beta,\Theta|\alpha,\eta)=\prod_{t=1}^Tp(\Theta_t|\alpha)\prod_{i=1}^Kp(\beta_k|\eta)(\prod_{n=1}^NP(w_{t,n} | z_{t,n}, \beta_k) P(z_{t,n|\Theta_t}))P(w,Z,B,Θ∣α,η)=t=1∏T​p(Θt​∣α)i=1∏K​p(βk​∣η)(n=1∏N​P(wt,n​∣zt,n​,βk​)P(zt,n∣Θt​​))

上图中的 α 和 η 是狄利克雷分布的超参数，通过极大似然学习，分别决定了主题分布 $\Theta$ 和词分布 $\beta$ 。主题分布 $\Theta$ 是一个维度为文档数 × 主题数的矩阵，矩阵元素 θi,j\theta_{i,j}θi,j​ 是主题 j 在文档 i 中的比例；词分布 $\beta$ 是一个维度为主题数 × 词数的矩阵，矩阵元素 βi,j\beta_{i,j}βi,j​ 是词 j 在主题 k 中的频次。在这个模型中，只有文档分布 w 是观测变量。文档分布 $w$ 是一个维度为文档数 × 词数的矩阵，矩阵元素 wi,jw_{i,j}wi,j​ 是词 j 在文档 i 中出现的频次。

求解主题分布和词分布，用Gibbs Sampling。首先随机初始化，多次遍历每个词，用其他所有词来预测它，逐渐收敛，获得近似解。

使用 LDA，可以从文档语料库中提取人类可解释的主题，其中每个主题都以与之关联度最高的词语作为特征。例如，主题 2 可以用诸如「石油、天然气、钻井、管道、楔石、能量」等术语来表示。此外，在给定一个新文档的条件下，我们可以获得表示其主题混合的向量，例如，5％ 的主题 1，70％ 的主题 2，10％的主题 3 等。通常来说，这些向量对下游应用非常有用。

Reference：

• 《深度学习进阶-NLP》，p63-94
• 《百面机器学习》p133-138
• 《西瓜书》p337-339
• 一文读懂如何用LSA、PSLA、LDA和lda2vec进行主题建模
• 浅谈话题模型：LSA、PLSA、LDA
• topic model (LSA、PLSA、LDA)