维特比算法

维特比算法（Viterbi algorithm）是在一个用途非常广的算法，本科学通信的时候已经听过这个算法，最近在看 HMM（Hidden Markov model） 的时候也看到了这个算法。于是决定研究一下这个算法的原理及其具体实现，如果了解动态规划的同学应该很容易了解维特比算法，因为维特比算法的核心就是动态规划。

对于 HMM 而言，其中一个重要的任务就是要找出最有可能产生其观测序列的隐含序列。一般来说，HMM问题可由下面五个元素描述

1
2
3
4
5

观测序列（observations）：实际观测到的现象序列
隐含状态（states）：所有的可能的隐含状态
初始概率（start_probability）：每个隐含状态的初始概率
转移概率（transition_probability）：从一个隐含状态转移到另一个隐含状态的概率
发射概率（emission_probability）：某种隐含状态产生某种观测现象的概率

下面以***上的具体例子来说明

想象一个乡村诊所。村民有着非常理想化的特性，要么健康要么发烧。他们只有问诊所的医生的才能知道是否发烧。 聪明的医生通过询问病人的感觉诊断他们是否发烧。村民只回答他们感觉正常、头晕或冷。
假设一个病人每天来到诊所并告诉医生他的感觉。医生相信病人的健康状况如同一个离散马尔可夫链。病人的状态有两种“健康”和“发烧”，但医生不能直接观察到，这意味着状态对他是“隐含”的。每天病人会告诉医生自己有以下几种由他的健康状态决定的感觉的一种：正常、冷或头晕。这些是观察结果。 整个系统为一个隐马尔可夫模型(HMM)。
医生知道村民的总体健康状况，还知道发烧和没发烧的病人通常会抱怨什么症状。 换句话说，医生知道隐马尔可夫模型的参数。则这些上面提到的五个元素表示如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

states = ('Healthy', 'Fever')
 
observatiOns= ('normal', 'cold', 'dizzy')
 
start_probability = {'Healthy': 0.6, 'Fever': 0.4}
 
transition_probability = {
   'Healthy' : {'Healthy': 0.7, 'Fever': 0.3},
   'Fever' : {'Healthy': 0.4, 'Fever': 0.6},
   }
 
emission_probability = {
   'Healthy' : {'normal': 0.5, 'cold': 0.4, 'dizzy': 0.1},
   'Fever' : {'normal': 0.1, 'cold': 0.3, 'dizzy': 0.6},
   }

其对应的状态转移图如下所示

现在的问题是假设病人连续三天看医生，医生发现第一天他感觉正常，第二天感觉冷，第三天感觉头晕。 于是医生产生了一个问题：怎样的健康状态序列最能够解释这些观察结果。维特比算法解答了这个问题。

首先直观地看这个问题，在HMM中，一个观测现象后面的对应的各个状态都有一个概率值，我们只需要选择概率值最大的那个状态即可，但是这个概率值是跟前面一个状态有关的（马尔科夫假设），因此不能独立考虑每个观测现象。

为了从时间复杂度方面进行比较，现在将问题一般化：假设观测序列的长度为 m，隐含状态个数为 n。则有下面的隐含状态转移图（下图为了便于表示，将只画出n = 3 的图）。

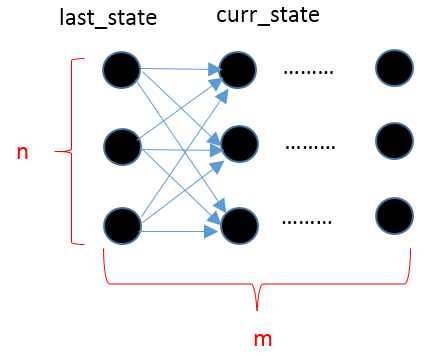
假如采用穷举法，穷举出所有可能的状态序列再比较他们的概率值，则时间复杂度是 O(m∗n2)

从动态规划的问题去考虑这个问题，根据上图的定义，记 last_state 为上一个观测现象对应的各个隐含状态的概率，curr_state 为现在的观测现象对应的各个隐含状态的概率。则求解curr_state实际上只依赖于last_state。而他们的依赖关系可通过下面的 python 代码表示出来

1
2
3
4
5

for cs in states:
    curr_state[cs] = max(last_state[ls] * 
                         transition_probability[ls][cs] *             
                         emission_probability[cs][observation] 
                         for ls in states)

计算过程利用了转移概率 transition_probability 和发射概率 emission_probability，选出那个最有可能产生当前状态 cs 的上一状态 ls。

除了上面的计算，同时要为每个隐含状态维护一个路径 path， path[s] 表示到达状态 s 前的最优状态序列。通过前面的计算选出那个最有可能产生当前状态 cs 的上一状态 ls后，往path[cs] 中插入 ls。则依照这种方法遍历完所有的观测序列后，只需要选择 curr_state 中概率值最大的那个 state 作为最终的隐含状态，同时从 path 中取出 path[state] 作为该最终隐含状态前面的状态序列。

从上面的分析可知，观测序列只需要遍历一遍，时间复杂度为 O(m∗n2).

假如在 NLP 中应用 HMM，则将词序列看做是观测到的现象，而词性、标签等信息看做是隐含状态，那么就可以通过维特比算法求解其隐含状态序列，而这也是 HMM 在分词，词性标注，命名实体识别中的应用。其关键往往是找出上面提到的初始概率（start_probability）、转移概率（transition_probability）、发射概率（emission_probability）。

而在通信领域中，假如将收到的编码信息看作是观测序列，对应的解码信息为隐含状态，那么通过维特比算法也能够找出概率最大的解码信息。

需要注意的是维特比算法适用于多步骤多选择的最优问题，类似于下面的网络，《数学之美》中将其叫做“篱笆网络(Lattice)”。每一步都有多个选择，并且保留了前面一步各个选择的最优解，通过回溯的方法找到最优选择路径。

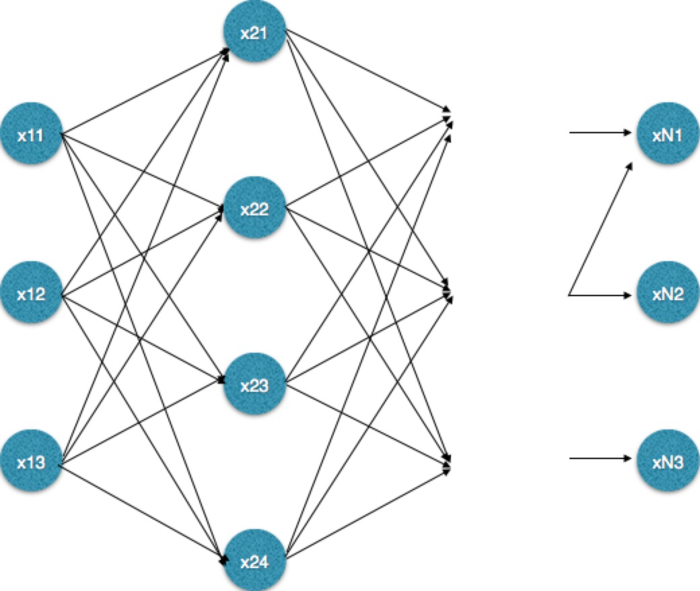
这里要强调的是 viterbi 算法可以用于解决 HMM 问题，但是也可以用于解决其他符合上面描述的问题。

最后，上文中的完整的代码见这里

参考：
维特比算法