 神经网络(Neural networks,NN)在过去十年来硕果累累,推动了整个行业的机器学习进程。然而,虽然许多神经网络在一些任务中表现相当出色,但网络本质上是一个复杂的系统,之前的研究已经分析了神经网络训练的过程,但它在很大程度上仍然是一个黑盒子,我们对其训练和操作模式仍然知之甚少。因此,产学研界都在为更好地理解网络属性和模型预测而不懈努力。
神经网络(Neural networks,NN)在过去十年来硕果累累,推动了整个行业的机器学习进程。然而,虽然许多神经网络在一些任务中表现相当出色,但网络本质上是一个复杂的系统,之前的研究已经分析了神经网络训练的过程,但它在很大程度上仍然是一个黑盒子,我们对其训练和操作模式仍然知之甚少。因此,产学研界都在为更好地理解网络属性和模型预测而不懈努力。
针对这个问题,Uber 在论文中提出了一种称为损失变化分配 (Loss Change Allocation,LCA)的方法,为神经网络训练过程提供了丰富的观察窗口,有望提高神经网络的可解释性。

作者 | Janice Lan,Rosanne Liu等
译者 | 清儿爸
责编 | 夕颜
在 Uber,工程师们将神经网络用于各种目的,包括检测和预测自动驾驶车辆的目标运动,更快地响应客户,以及构建更好的地图。
在神经网络训练过程中,尽管数以百万计的参数在训练期间可以通过简单的规则进行调整,但我们对过程本身的看法仍然局限于标量损失量,这严重限制了我们对丰富、高维处理过程的了解。例如,可能网络的一部分正在执行所有的学习,而另一部分却是无用的,但是仅仅观察损失,永远不会揭示这一点。
在 Uber 的论文《LCA:神经网络训练的损失变化分配》(LCA: Loss Change Allocation for Neural Network Training)中,Uber 提出的 LCA 方法可以将损失的变化分配给各个参数,从而度量每个参数的学习量。使用 LCA,Uber 提出了三个关于神经网络有趣的观察,包括噪音、层贡献和层同步。

LCA方法详解
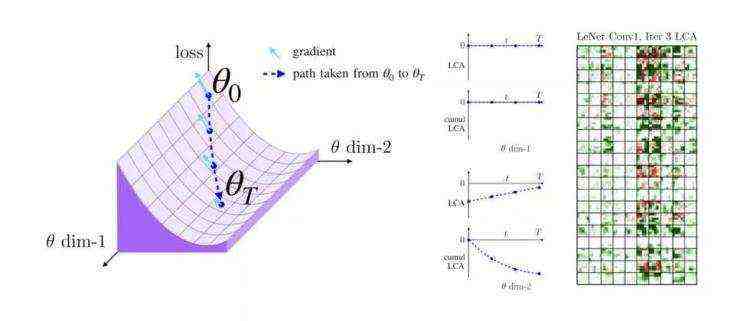
揭示神经网络训练过程的详细见解的一种方法是,度量神经网络的每个可训练参数在任何时间点的学习量。此处 Uber 将“学习”视为对网络的改变,从而降低训练集的损失。请注意,他们考虑的是整个训练集的损失,而不仅是一批;在 SGD 中,虽然批量驱动参数更新,但他们衡量的是整个训练集的学习。
假设正在训练一个网络,在一次训练迭代中,参数向量从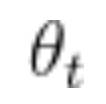 移动到
移动到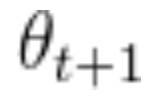 。由于这一运动,损失从 1.85 减少到 1.84。在这种
。由于这一运动,损失从 1.85 减少到 1.84。在这种 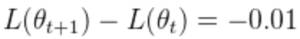 情况下,可以说网络“学会了”将损失减少 0.01。我们可以通过一阶泰勒级数来近似这种损失的变化:
情况下,可以说网络“学会了”将损失减少 0.01。我们可以通过一阶泰勒级数来近似这种损失的变化:
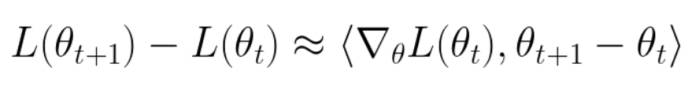
一个与我们可以直接计算近似的量似乎毫无意义,但近似并非 Uber 的最终目标:Uber 用近似来将标量损失的变化分解成单个的分量。在这种情况下,方程的右侧是两个向量的点积,其长度等于参数的数量。Uber 可以将这个点积分解成它的分量总和:
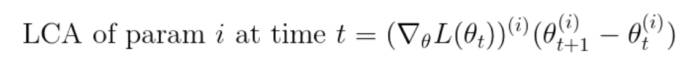
其中, 是参数向量或梯度向量上的索引。通过在每个训练迭代中对此进行度量,能够将标量损失的变化分配给各个参数。Uber 将其称为损失变化分配(Loss Change Allocation,LCA):参数在迭代中的移动造成的损失上升或下降的程度。下面是 LCA 的一些直观属性:
是参数向量或梯度向量上的索引。通过在每个训练迭代中对此进行度量,能够将标量损失的变化分配给各个参数。Uber 将其称为损失变化分配(Loss Change Allocation,LCA):参数在迭代中的移动造成的损失上升或下降的程度。下面是 LCA 的一些直观属性:
如果参数具有零梯度或者不移动,那么它的 LCA 为零,如图 1b 所示。
如果参数具有非零梯度并沿着负梯度方向移动,那么它具有负 LCA,如图 1c 所示。Uber 称这些参数为“帮助”,因为它们减少了迭代中的损失。
如果参数沿着梯度的正方向移动,它就会因为增加损失而“受伤”。这可能是由于嘈杂的小批量或动量导致的参数移动错误方向引起的。
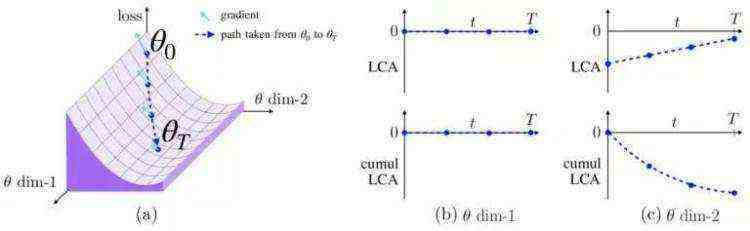
LCA 分量具有很好的接地特性,这意味着它们是损失的实际变化的总和(对近似方法作了一些修改,考虑了曲率,并保证精度,正如 Uber 在论文所揭示的那样)。在整个训练过程中,度量每个参数和迭代的 LCA。对参数进行求和,将得到每次迭代的总损失变化量;如果对迭代进行求和,将得到每个参数的总 LCA。

通过训练显微镜进行可视化
有了如上所述定义的 LCA 度量,Uber 就可以将其作为显微镜,用于训练数据集(例如 MNIST 或 CIFAR-10)的一些示例网络的训练过程。对于 MNIST,Uber 训练了两个网络:FC(一个三层全连接网络)和 LeNet(一个带有两个卷积层,然后是两个全连接层的网络)。对于 CIFAR-10,Uber 训练了 ResNet(一个 20 层的残差网络)。本文中所有的网络都使用 SGD 进行训练(要了解其他网络和优化器的结果,请参阅 Uber 的论文)。
在下面的视频中,Uber 将直接对 LCA 数据进行可视化,每个帧给定迭代中所有参数的 LCA。FC 在本例中表示,每个像素代表一个参数,以层的形式布置。
视频 1. Uber在 MNIST 上为 FC 训练的前 400 次迭代制作了动画。绿色表示负 LCA(帮助),红色表示正 LCA(受伤)。
在上面的视频中,Uber看到了一些趋势:
迭代 1-10:在开始时,损失急剧下降,Uber看到许多绿色参数。
迭代 10-100:经过几次迭代之后,Uber看到绿色和红色的嘈杂混合,表明一些参数是有帮助的,而另一些参数正在受伤。
迭代 100+:一旦损失接近其最终值,Uber看到大多数像素接近白色,表明参数不再具有明显的帮助或伤害。
本文的第 S2 节提供了更多直接可视化的示例。这样的可视化很吸引人,可以帮助表面缺陷或识别死亡的神经元和无用的参数,但很难从中得出更多的定量结论。为了更好地理解更高级别的 LCA 模式,Uber 接下来尝试一些定量聚合。

结果 1:训练很嘈杂
Uber 考虑的第一个聚合是 LCA 值在所有参数和所有迭代上的分布。下面的图 2 显示了 ResNet 的 LCA 分布,其中绿色条表示有助于损失的分量,红色条表示伤害损失的分量:
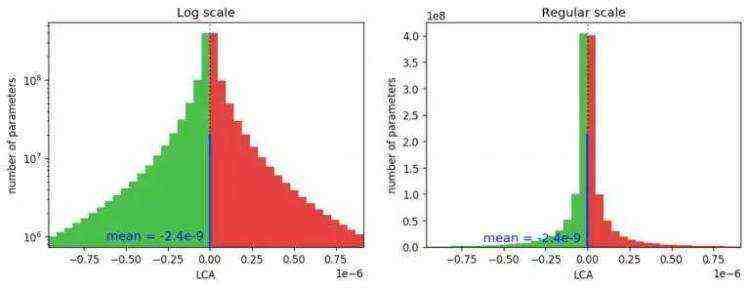
图 2. 显示所有 LCA 元素分布情况的直方图(所有迭代中的所有参数),显示只有不到一半是负数(帮助)。相应的直方图以对数刻度(左)显示,以查看分布的尾部和常规刻度(右),以便更清楚地显示负 / 正比率。
LCA 分布有几个有趣的属性。在绘制这张图之前,Uber 已经知道这个分布的均值是多少:平均 LCA 仅为(总损失变化)/(参数数量 x 训练步骤数量)。对于图 2 中的运行,平均值为 -2.4e-9,用蓝线高亮显示。假设平均值是 -2.4e-9,Uber可能已经预期在该值附近会有一个狭窄的正态分布。相反,他们看到的是一个非常广泛的分布。事实上,它是如此之宽,以至于在这种细节层面上,它的均值与 0 无法区分。这意味着,并非所有的网络参数都在单一方向上移动,将网络推向更低的损耗,而是在训练过程中充满了帮助和受伤的参数之间的竞争。LCA 也是重尾分布的:如果它是正态分布的,那么对数空间中的直方图就会呈现出倒抛物线的形状。
Uber 可以通过计算帮助(绿色)而不是受伤(红色)的权重百分比来量化这种张力。他们发现,在给定的迭代中,只有 80.7% 的权重对该网络有帮助。换言之,在任何给定的时间里,所有参数只有不到一半对网络训练是有帮助的,其余的参数都朝着错误的方向移动!
令人惊讶的是,正 LCA 参数朝着错误的方向移动,这引发了一些额外的问题:
随着训练网络的时间越来越长,损失最终会停止下降,可以想象,有帮助的参数百分比将会收敛到 50%。因此,他们不禁要问:这个接近 50% 的比例,仅仅是否因为网络训练时间过长而产生的?然而,下面的图 3a 表明,情况并非如此:在训练期间的大多数时间点,这个比率仅略高于 50%,在最速学习的早期迭代中,这一比例略高,但仍然低于 60%。
其次,鉴于许多函数的帮助被许多参数的伤害所抵消,那么一些参数是否一直在“帮忙”,如果是,它们是否一直被其他参数的伤害所抵消?换句话说,是否有一些“英雄”参数几乎一直在帮助,而“恶棍”参数却不断造成伤害?但图 3b 显示并非如此:帮助最多的参数通常在 53% 的时间内有帮助,而帮助最少的参数仍然有 48% 的时间帮助。
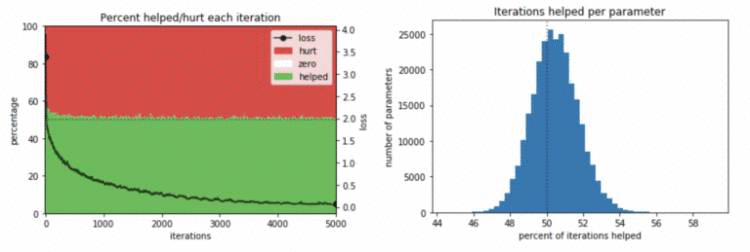
图 3. 研究发现:(a) 在所有迭代中,参数的帮助率接近 50%;(b) 所有参数的帮助大约为一半时间。
这两个观察结果在很大程度上可以解释为训练中普遍存在的震荡现象。在下面的图 4 中,Uber展示了两个示例参数随时间变化的运动、底层梯度和结果 LCA。在这些图标中,可以清楚看到震荡现象:
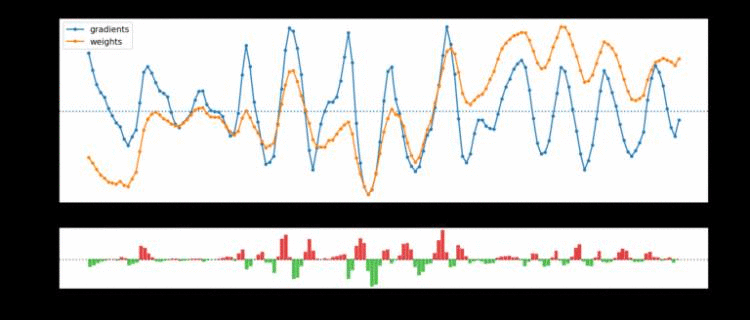
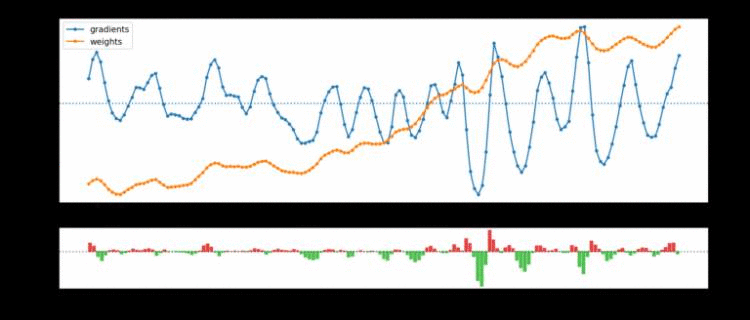
图 4. 显示了 ResNet 最后一层的两个参数:在给定的迭代过程中,一个参数伤害最大(顶部),另一个参数帮助最大(底部)(net LCA 分别为 +3.41e-3 和 -3.03e-3)。权重(橙色)和梯度(蓝色)轨迹都在震荡,导致 LCA(绿色和红色)在帮助和伤害之间交替。
除了震荡权重和梯度之外,图 4 还揭示了参数的运动和底层梯度有同时波动的趋势。这表明震荡是由于参数在局部极小值上来回摆动所致,与小批量噪声驱动无关。
虽然图 4 中只显示了两个参数,但震荡在整个训练和整个网络中是普遍存在的。例如,在所描述的运行期间,权重值平均每 7 次迭代改变方向,梯度每 10 次迭代改变符号。事实上,即使调整学习率、批量大小和动量值,使网络能够合理地训练,仍然可以观察到震荡普遍存在,并测量出近一半的参数会受到伤害(详情请参阅 Uber 的论文)。
通过这些实验,LCA 揭示了关于神经网络训练的第一个见解:在任何给定的时间,几乎将近一半的参数都会受到伤害,或者在训练梯度上出现偏差。网络之所以能够进行整体学习,只是因为许多有噪声的 LCA 分量的平均值略微为负。

结果 2:有些层是向后的
Uber 不仅可以使用自己方法来研究低层次的、每个参数的 LCA,也可以在更高层次的分解上聚合 LCA。Uber 期望,通过这种方式能够看到不同的见解;在参数级别上有很多噪音,但总体来说,网络是有学习能力的。聚合 LCA 的一种方法是对每一层中所有参数和所有时间进行求和。这可以度量每一层在训练过程中的学习量,如下面的图 5 中两个网络所示:
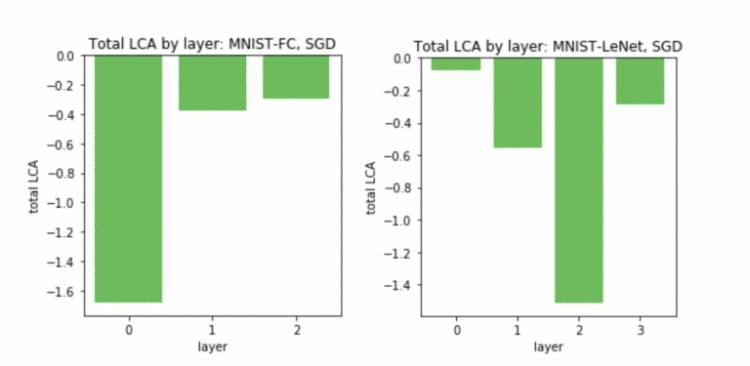
图 5. Uber对 FC(左)和 LeNet(右)的每个层中的所有参数进行 LCA 求和。不同的层学习不同的数量,每层 LCA 的差异主要可以通过层中参数的数量来解释。
如果按照参数的数量将每一层的 LCA 进行归一化,不出意外的话,我们会看到相反的效果,其中较小的层的参数平均具有更多的 LCA。接下来,我们来看看 ResNet 是否表现出不同的行为:
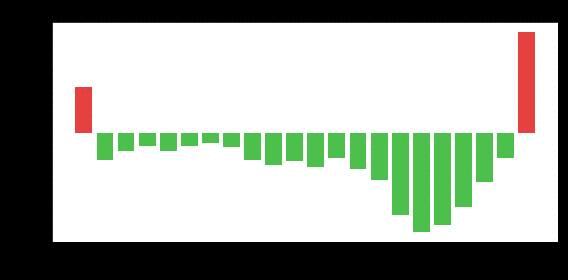
图 6.ResNet 揭示了一个不同的模式:第一层和最后一层具有正 LCA,这意味着它们的移动实际上增加了训练过程的损失。这很让人惊讶,因为网络总体上是有学习能力的,而且对于一大组参数的 LCA 总和而言,持续为正是没有意义的。
虽然 FC 和 LeNet 并没有给出任何令人惊讶的结论&#xff0c;但 Uber 注意到&#xff0c;ResNet 有些不正常。第一层和最后一层具有正 LCA&#xff0c;这意味着它们的移动实际上增加了训练过程中的损失&#xff01;虽然他们已经观察到个别参数受到伤害&#xff0c;但Uber预计在大群体上进行总和时&#xff0c;LCA 将为负&#xff0c;因为平均 LCA 为负。然而&#xff0c;对于这些有害的层来说&#xff0c;情况并非如此&#xff0c;它们每次运行时&#xff0c;LCA 始终为正&#xff08;并且 10 次运行时 p-value <1e-4&#xff09;。
对于这个奇怪的结果&#xff0c;Uber 想知道&#xff1a;如果一个层受伤了&#xff0c;那么在初始化时就冻结该层会怎么样呢&#xff1f;通过阻止权重移动&#xff0c;Uber 就可以阻止让它受到伤害或帮助。这会让网络整体表现变得更好吗&#xff1f;Uber 在第一层尝试了这项技术&#xff0c;但最终的损失并没有变得更好&#xff1a;即使阻止了第一层的伤害&#xff0c;其他的层也没能起到同样的作用。因此&#xff0c;尽管 LCA 为正&#xff0c;但第一层的参数移动是很重要的。然而&#xff0c;如果冻结最后一层&#xff08;如图 7 所示&#xff09;&#xff0c;它将提高整体网络性能&#xff0c;从而降低整体损失。

图 7. Uber 展示了 ResNet 中每层的 LCA&#xff0c;用于常规训练场景&#xff08;实心柱&#xff09;&#xff0c;以及在初始化时冻结最后一层&#xff08;阴影线&#xff09;的场景&#xff0c;平均每个场景超过 10 次运行。通过冻结最后一层&#xff0c;Uber可以防止它受到伤害。虽然其他层的帮助没有那么多&#xff08;LCA 的负面影响较小&#xff09;&#xff0c;但最后一层 LCA 的变化弥补了这一点&#xff0c;从而降低了整体损失&#xff08;图右&#xff09;。
这些结果表明&#xff0c;最后一层最好要冻结。先前的研究已经发现冻结最后一层或者用不同的方法对其进行不同的处理是有好处的。LCA 提供了原则性的提示&#xff0c;即冻结最后一层可能会更好&#xff0c;同时也解释了它最初的问题所在&#xff1a;它普遍地受到了伤害。
为了理解为何一个层会首先受到伤害&#xff0c;Uber 考虑了一些可能的原因。小批量梯度是整个训练集梯度的无偏估计&#xff0c;因此&#xff0c;小批量噪声本身并不能解释总 LCA 为何为正。Uber 之前观察到的参数震荡现象是另一种可能的解释&#xff0c;但如果没有其他因素的话&#xff0c;震荡不应该导致在错误的方向上的漂移&#xff0c;因此这也不能解释为何总 LCA 为正。
在排除这些选项之后&#xff0c;Uber 假设解释与不同层对优化器相应的速度有关。如果由于各种因素的收敛&#xff0c;各层以不同的延迟进行学习&#xff0c;那么最后一层可能会一直滞后于其他层&#xff0c;与其他层稍微不同步。由于层间竞争以减少损失&#xff0c;延迟的最后一层可能会丧失收集 LCA 的能力。
幸运的是&#xff0c;Uber 可以通过优化器的动量直接调整每个层的延迟来检验这个假设是否正确。由于动量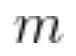 是过去梯度的指数加权平均值&#xff0c;因此 Uber 使用的平均梯度是
是过去梯度的指数加权平均值&#xff0c;因此 Uber 使用的平均梯度是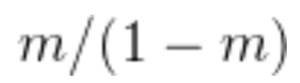 迭代的。到目前为止&#xff0c;Uber 对每一层都使用了动量 0.9&#xff0c;对应 9 次迭代的延迟。动量为 0 时&#xff0c;延迟则为 0。如果减少最后一层的动量&#xff0c;就能够减少最后一层相对于其他层的延迟。
迭代的。到目前为止&#xff0c;Uber 对每一层都使用了动量 0.9&#xff0c;对应 9 次迭代的延迟。动量为 0 时&#xff0c;延迟则为 0。如果减少最后一层的动量&#xff0c;就能够减少最后一层相对于其他层的延迟。
Uber 可以在不同的最后一层延迟级别下运行同一个网络&#xff0c;从 0 到 9 次进行迭代&#xff0c;而保持所有其他层的持续延迟为 9。正如假设的那样&#xff0c;最后一层的延迟越少&#xff0c;它的帮助就越大&#xff01;从伤害到帮助的转变几乎与延迟成线性关系。此外&#xff0c;由于其他层相对于最后一层的延迟更大&#xff0c;它们会因为现在的滞后和最后一层向前推进而受到更大的伤害&#xff0c;如下图 8 所示&#xff1a;
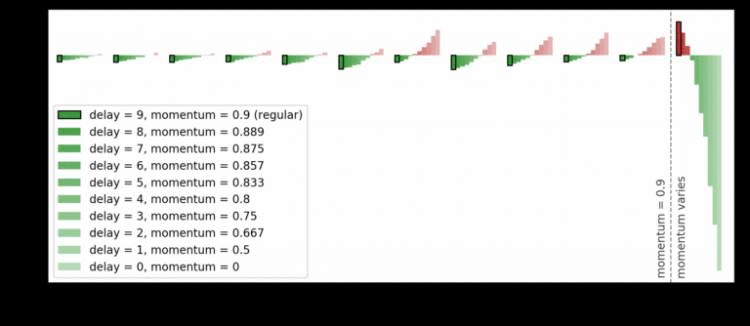
图 8. Uber 为最后一层训练了一个具有不同动量的 ResNet&#xff0c;并为每层绘制了总 LCA&#xff08;为了更好的可视化效果&#xff0c;省略了前十层&#xff09;。随着最后一层动量的减少&#xff0c;梯度新区驱动学习相对于其他层的延迟减小&#xff0c;最后一层的 LCA 以其他层的损失为代价向前推进。
从这些实验中&#xff0c;LCA 揭示了不同层的行为是不同的&#xff0c;有些层甚至在平均水平上逆着梯度移动&#xff0c;并受到伤害。通过信息延迟的角度来看训练&#xff0c;似乎是有效的。总之&#xff0c;这些结果表明&#xff0c;对每层进行优化调整可能是有益处的。

层是同步的
现在&#xff0c;Uber 已经了解了每一层的整体学习情况&#xff0c;下一步自然是研究不同层何时进行学习。先前的研究已经发现了层表示的广泛手链模式&#xff0c;但通过使用 LCA&#xff0c;Uber 可以在较小的范围内检查层间的学习。
LCA 方法的一个有用的特性是&#xff0c;它让研究人员可以分析他们所关心的任何损失函数。Uber 可以利用这一点&#xff0c;将训练集的损失分解成 10 个单独的损失&#xff08;每个真相类 1 个&#xff09;&#xff0c;画出更加细化的训练过程视图&#xff0c;使 Uber 能够确定每一层何时学习对分类有用的概念&#xff08;在这种情况下&#xff0c;是 MNIST 的每个类&#xff09;。
为了精确定位最高时间分辨率的学习&#xff0c;Uber 将层和类的“学习峰值时刻”定义为该层和类的 LCA 的局部最小值。换句话说&#xff0c;该类的损失由于该层在迭代 t 上的移动而减少&#xff0c;而非由于 t&#43;1 或 t-1 的移动而减少。
在下面的图 9 中&#xff0c;Uber 为 MNIST-FC 的每个层和每个类绘制了学习的前 20 个峰值时刻&#xff1a;

图 9. Uber 将 MNIST-FC 的“学习峰值时刻”按层和类进行可视化&#xff0c;每个点代表特定类和层的 LCA 峰值&#xff0c;其中网络中的三个层显示为三个堆叠的点。当所有个层的学习在同一次迭代中排列起来时&#xff0c;Uber 用红色标出这些点。
奇怪的是&#xff0c;研究人员经常在一条直线上看到三个点的集合&#xff08;以红色高亮表示可见性&#xff09;&#xff0c;这意味着所有三个层都在完全相同的迭代中为同一个类学习了一些东西。假设层是独立进行的&#xff0c;那么精确排列的学习峰值时刻的平均数量明显要高于预期的数量 (p <0.001)。
这些点的同步不能简单地使用单个批次在网络中引起大的同步变化来解释&#xff0c;因为虽然权重运动也是同步的&#xff08;见 Uber 论文中图 S18&#xff09;&#xff0c;但峰值权重运动和峰值 LCA 的迭代通常不会重合。每层和类的渐变也是同步的&#xff08;见论文的图 S15&#xff09;&#xff0c;这是另一个令人惊讶的观察结果&#xff1a;对于同一次迭代的所有层&#xff0c;每类训练集的损失会变得非常大&#xff0c;这无疑有助于时同步学习成为可能。
这就引出了 Uber 最后的结论&#xff1a;层学习在微观尺度上是同步的。

总结和展望
Uber 已经介绍了损失变化分配&#xff08;LCA&#xff09;方法&#xff0c;并通过以各种方式聚合 LCA 来证明&#xff0c;他们可以发现训练过程中的噪声&#xff0c;发现某些层对梯度的奇异流动&#xff0c;并揭示增量学习的跨层同步。
在论文中&#xff0c;Uber 详细阐述了这些发现&#xff0c;分析了更多的网络和优化器&#xff0c;并讨论了这项工作的前景。例如&#xff1a;
到目前为止讨论的所有实验都使用了训练集。如果Uber 也 跟踪验证 LCA&#xff0c;可以比较训练 LCA 和验证 LCA 来度量哪些参数导致了过拟合。这种分析可以实现有针对性的正则化。
LCA 可用于识别没有帮助的权重&#xff0c;因此是修剪或重新初始化的目标。除了识别要冻结的层之外&#xff0c;LCA 还可能是一个重要的诊断工具&#xff0c;用于识别次优超参数或配置不良的网络结构。
更好的优化器可能能够考虑到频繁的参数级的震荡现象&#xff0c;或者实现每层可调的超参数。
LAC 的可能性多种多样&#xff0c;可用于任何参数化模型。如果你对这项工作感兴趣&#xff0c;可详读完整论文&#xff0c;并咋你自己的网络下试验一下代码。
论文链接&#xff1a;https://eng.uber.com/research/lca-loss-change-allocation-for-neural-network-training/
GitHub 代码&#xff1a;https://github.com/uber-research/loss-change-allocation
【END】
60s测试&#xff1a;你是否适合转型人工智能&#xff1f;
https://edu.csdn.net/topic/ai30?utm_source&#61;csdn_bw

热 文 推 荐


 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有