图论模型-Floyd 算法

1. 引例

某公司在六个城市C C 1 1 ,C 2 2 ,C 3 3 ,C 4 4 ,C 5 5 ,C 6 6 都有分公司&＃xff0c;
公司成员经常往来于它们之间&＃xff0c;已知从 Ci 到C C j j 的直达航
班票价由下述矩阵的第i i 行&＃xff0c;第j j 列元素给出&＃xff08;∞ ∞ 表示无
直达航班&＃xff09;&＃xff0c;该公司想算出一张任意两个城市之间的最
廉价路线航费表。

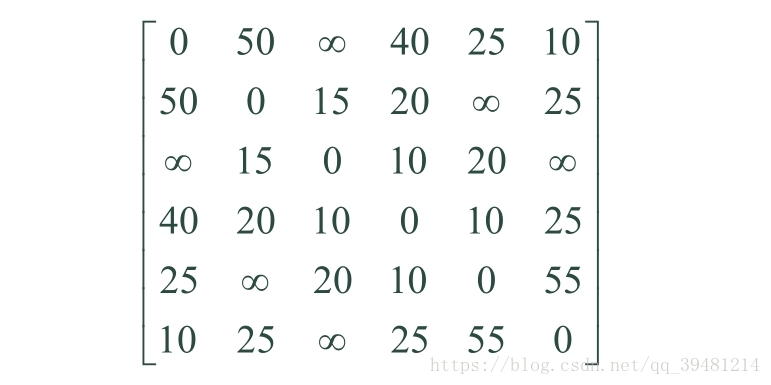
1.1 矩阵解释

第一行&＃xff1a;&＃xff08;1&＃xff0c;1&＃xff09;&＃61;> 第一个城市到第一个城市的费用为 0
&＃xff08;1&＃xff0c;2&＃xff09; &＃61;> 第一个城市到第二个城市的费用为 50
&＃xff08;1.&＃xff0c;3&＃xff09; &＃61;> 第一个城市到第三个城市的费用为 无穷大&＃xff0c;即不能直接到达。
以此类推…

2. Floyd算法思想

算法思想原理&＃xff1a;

Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话&＃xff0c;首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题&＃xff0c;我们需要为这个目标重新做一个诠释&＃xff08;这个诠释正是动态规划最富创造力的精华所在&＃xff09;

从任意节点i到任意节点j的最短路径不外乎2种可能&＃xff0c;1是直接从i到j&＃xff0c;2是从i经过若干个节点k到j。所以&＃xff0c;我们假设Dis(i,j)为节点u到节点v的最短路径的距离&＃xff0c;对于每一个节点k&＃xff0c;我们检查Dis(i,k) &＃43; Dis(k,j) j的路径短&＃xff0c;我们便设置Dis(i,j) &＃61; Dis(i,k) &＃43; Dis(k,j)&＃xff0c;这样一来&＃xff0c;当我们遍历完所有节点k&＃xff0c;Dis(i,j)中记录的便是i到j的最短路径的距离。

3. 通用代码

3.1代码块一&＃xff1a;

tulun2.ma&＃61; [ 0,50,inf,40,25,10;50,0,15,20,inf,25;inf,15,0,10,20,inf;40,20,10,0,10,25;25,inf,20,10,0,55;10,25,inf,25,55,0];% 只需修改举证即可
[D, path]&＃61;floyd(a)

3.2 代码块二&＃xff1a;

floyd.mfunction [D,path,min1,path1]&＃61;floyd(a,start,terminal)
D&＃61;a;n&＃61;size(D,1);path&＃61;zeros(n,n);
for i&＃61;1:nfor j&＃61;1:nif D(i,j)~&＃61;infpath(i,j)&＃61;j;end, end,
end
for k&＃61;1:nfor i&＃61;1:nfor j&＃61;1:nif D(i,k)&＃43;D(k,j)i,j)D(i,j)&＃61;D(i,k)&＃43;D(k,j);path(i,j)&＃61;path(i,k);end, end, end,
end
if nargin&＃61;&＃61;3min1&＃61;D(start,terminal);m(1)&＃61;start;i&＃61;1;path1&＃61;[ ]; while path(m(i),terminal)~&＃61;terminalk&＃61;i&＃43;1; m(k)&＃61;path(m(i),terminal);i&＃61;i&＃43;1;endm(i&＃43;1)&＃61;terminal;path1&＃61;m;
end

4. 结果分析&＃xff1a;

D &＃61;0 35 45 35 25 1035 0 15 20 30 2545 15 0 10 20 3535 20 10 0 10 2525 30 20 10 0 3510 25 35 25 35 0path &＃61;1 6 5 5 5 66 2 3 4 4 65 2 3 4 5 45 2 3 4 5 61 4 3 4 5 11 2 4 4 1 6

4.1 解析&＃xff1a;

D: 城市间最短费用&＃xff08;距离等&＃xff09;
PATH : 城市间最短费用&＃xff08;距离等&＃xff09;对应的路线。
例如&＃xff08;2&＃xff0c;5&＃xff09;城市二到城市五 。观察path矩阵 &＃xff1a;要经过城市四&＃xff0c;即2->4->5。再根据(2,4)对应4, (4,5)对应5&＃xff0c;故最佳路线为2->4->5
观察D矩阵&＃xff1a;&＃xff08;2&＃xff0c;5&＃xff09;对应值30&＃xff0c;则最便宜费用30。

5. 图论模型-Floyd 算法与图论模型-Dijkstra不同

我们使用Floyd算法来计算上面引例 城市二到城市五&＃xff1a;

5.1主代码快一&＃xff1a;

weight&＃61; [ 0,50,inf,40,25,10;50,0,15,20,inf,25;inf,15,0,10,20,inf;40,20,10,0,10,25;25,inf,20,10,0,55;10,25,inf,25,55,0;];
[dis, path] &＃61; dijkstra(weight,2, 5)

5.2 函数代码块一样

5.3 结果

dis &＃61;30path &＃61;2 4 5

5.4 分析

最低费用30&＃xff0c;最佳路线&＃xff1a;2->4->5。 此结果和floyd算法结果一致。
所以我们可以很容易发现他们的不同了吧。

Floyd&＃xff1a;能一次性显示所有路线问题。
Dijkstra&＃xff1a;能显示一条规定的最佳路线&＃xff0c;和最佳值&＃xff0c;较直观。

通常在建模中&＃xff0c;两种算法应该都使用&＃xff0c;这样能互相证明&＃xff0c;更具有说服力。也能为论文加分。