接上一节Tarjan算法初探(2):缩点
在此首先提出几个概念&＃xff1a;
割点集合&＃xff1a;一个无向连通图G 若删除它的一个点集 以及点集中所有点相连的边(任意一端在点集中)后 G中有点之间不再连通则称这个点集是它的一个割点集合
割边集合&＃xff1a;一个无向连通图G 若删除它的一个边集 G中有点之间不再连通则称这个边集是它的一个割边集合
图的点联通度&＃xff1a;无向连通图的最小割点集合中元素的个数是一张无向连通图的点连通度
图的边联通度&＃xff1a;无向连通图的最小割边集合中元素的个数是一张无向连通图的边联通度
割点&＃xff1a;如果一个无向连通图的点连通度为1 那么割点集合中唯一的点就是割点
桥&＃xff1a;如果一个无向连通图的边连通度为1 那么割边集合中唯一的边就是桥
点双连通&＃xff08;或复连通&＃xff09;&＃xff1a;无向连通图的点连通度大于1
边双连通&＃xff08;或复连通&＃xff09;&＃xff1a;无向连通图的边连通度大于1
点双连通子图&＃xff1a;G&＃39;是点双连通的 G&＃39;是G的子图 则G&＃39;是G的一个点双连通子图
点双连通分量&＃xff1a;G&＃39;是G的一个点双连通子图 同时G&＃39;不是G的点双连通子图的真子集 那么G&＃39;就是一个极大点双连通子图 G&＃39;也是G的点双连通分量 点双连通分量又叫块
边双连通子图&＃xff1a;G&＃39;是边双连通的 G&＃39;是G的子图 则G&＃39;是G的一个边双连通子图
边双连通分量&＃xff1a;G&＃39;是G的一个边双连通子图 同时G&＃39;不是G的边双连通子图的真子集 那么G&＃39;就是一个极大边双连通子图 G&＃39;也是G的边双连通分量
概念有点多 但都很简单 希望仔细看完
下面讲割点与桥的求法&＃xff1a;
由割点的定义可知若在dfs搜索树中无向图的一个节点V是割点 当且仅当满足下面两个条件中任意一个时成立&＃xff1a;
1.V是根节点 则当它的子树个数多于1时 若子树个数小于等于1 则V此时不在两点间的路径上 V只能是一条路径的起点和终点 删除V不影响剩下的点之间的连通性
2.V不是根节点 且Low(u)>&＃61;Dfn(v)&＃xff0c;u∈v的子节点 Low(u)表示u及u的子树能够访问到的最早的点的dfs序 而Dfn(u)表示u的dfs序 由于无向图不存在两颗子树之间的连边 故Low(u)
代码具体实现&＃xff1a;
类似Tarjan求强连通分量 由于是无向图 故不需要判断一个点连接到已访问的点是不是在栈中(因为在无向图中一个点连接到已访问的点时这两个点必在同一棵子树内)且重边不影响割点的判断
同时
Low[u]&＃61;min(Low[u],Low[v]),v∈u的子节点
Low[u]&＃61;min(Low[u],dfn[v]),v∈u能连接到的已访问的点
下面贴代码
1 void tarjan(int now)
2 {
3 int tot&＃61;0;
4 low[now]&＃61;dfn[now]&＃61;&＃43;&＃43;k;
5 for(int i&＃61;h[now];i;i&＃61;e[i].nex)
6 {
7 if(!dfn[e[i].to])
8 tarjan(e[i].to),low[now]&＃61;min(low[now],low[e[i].to]),&＃43;&＃43;tot;
9 else
10 low[now]&＃61;min(low[now],dfn[e[i].to]);//更新Low
11 if(now&＃61;&＃61;root&&tot>1||now!&＃61;root&&low[e[i].to]>&＃61;dfn[now])
12 flag[now]&＃61;1;//割点的判断
13 }
14 }
在无向图中判断一条边(u,v)是桥 当且仅当(u,v)是搜索树上的一条边 且Low(u)>Dfn(v) 时成立 在这时(u,v)是u到v唯一路径 故删除(u,v) u,v不连通 此时重边会影响桥的判断 所以我们把一条无向边拆成编号相邻的边那么在实际操作中我们就可以判断一条边是重边还是原来边的反向边 反向边不能继续访问了 因为在Low(u)>Dfn(v)时判断割边 若走反向边会影响判断
代码类似求割点
再说下点双连通分量的求法 &＃xff1a;
事实上在求割点的同时可以顺便求出点双连通分量 维护一个栈在求割点的途中若Low(u)
代码不贴了
边双连通分量的求法更为简单
将求得的割边全部删除 剩下的所有连通块都是边连通分量 同时边连通分量不一定是点连通分量 但点连通分量一定是边连通分量除了下图所示的情况以外
删去 边&＃xff08;1,2&＃xff09; 图不再连通
对于有割边的无向连通图来说 更重要的是如何把通过加边使它的边连通度不再为1 这个问题相较于点连通分量来说更为复杂 故单独提出来分析一下&＃xff1a;
首先将所有删掉桥后的连通块视作一个点 再把桥边加回来得到的必定是一棵树 统计其中度为1的叶子点数为leaf 则最少需要添加(leaf&＃43;1)/2条边(leaf&＃61;&＃61;1时为0条)
若加的边满足如下情况&＃xff08;连接的两点之间有两条支链&＃xff09;则会使叶子节点减少1 否则不会使叶子节点数减少 &＃xff08;三个叶子需要两次&＃xff09;
连接1 5后重缩点 会使叶子节点减少1
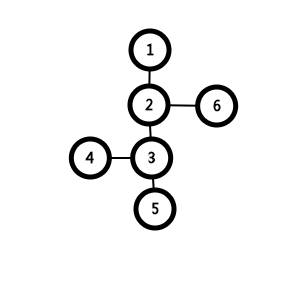
而我们的目标是使叶子节点数为1&＃xff0c;而每次操作会使叶子节点数减少1 减少到3时特判即可 最终得到规律&＃xff1a;最少要(leaf&＃43;1)/2条边(leaf&＃61;&＃61;1时为0条)
京公网安备 11010802041100号