搜索技术【广度优先搜索】简介分支限界法

搜索技术【广度优先搜索】 - 简介 & 分支限界法

【简介】

在图的应用中已讲过图的广度优先搜索&＃xff0c;树上的广度优先搜索实际上就是层次遍历。

首先遍历第1层&＃xff0c;然后第2层……同一层按照从左向右的顺序访问&＃xff0c;直到最后一层。一棵树如下图所示&＃xff0c;

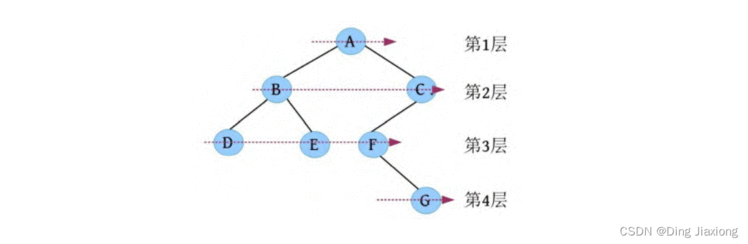
首先遍历第1层A&＃xff1b;然后遍历第2层&＃xff0c;从左向右遍历B、C&＃xff1b;再遍历第3层&＃xff0c;从左向右遍历D、E、F&＃xff1b;再遍历第4层G。

【分支限界法】

分支限界法通常以广度优先或以最小耗费&＃xff08;最大效益&＃xff09;优先的方式搜索问题的解空间树。

首先将根节点加入活节点表中&＃xff0c;接着从活节点表中取出根节点&＃xff0c;使其成为当前扩展节点&＃xff0c;一次性生成其所有孩子节点&＃xff0c;判断对孩子节点是舍弃还是保留&＃xff0c;舍弃那些得不到可行解或最优解的节点&＃xff0c;将其余节点保留在活节点表中。再从活节点表中取出一个活节点作为当前扩展节点。重复上述过程&＃xff0c;直到找到所需的解或活节点表为空时为止。每一个活节点最多只有一次机会成为扩展节点。活节点表的实现通常有两种形式&＃xff1a;一种是普通的队列&＃xff0c;即先进先出队列&＃xff1b;另一种是优先级队列&＃xff0c;按照某种优先级决定哪个节点为当前扩展节点。

根据活节点表的不同&＃xff0c;分支限界法分为以下两种&＃xff1a;队列式分支限界法和优先队列式分支限界法。

[解题秘籍]

① 定义解空间。

解空间的大小对搜索效率有很大的影响&＃xff0c;首先要定义合适的解空间&＃xff0c;确定解空间包括解的组织形式和显约束。解的组织形式规范为一个n 元组{x 1 ,x 2 ,…,xn }&＃xff0c;具体问题表达的含义不同。显约束是对解分量的取值范围的限定。

② 确定解空间的组织结构。

对解空间的组织结构通常用解空间树形象地表达&＃xff0c;根据解空间树的不同&＃xff0c;解空间分为子集树、排列树、m叉树等。

③ 搜索解空间。

分支限界法指按照广度优先搜索策略&＃xff0c;一次性生成所有孩子节点&＃xff0c;根据约束函数和限界函数判定对孩子节点是舍弃还是保留&＃xff0c;如果保留&＃xff0c;则将其依次放入活节点表中&＃xff0c;活节点表是普通队列或优先队列。然后从活节点表中取出一个节点&＃xff0c;继续扩展&＃xff0c;直到找到所需的解或活节点表为空时为止。如果对该问题只求可行解&＃xff0c;则只需设定约束函数即可&＃xff1b;如果求最优解&＃xff0c;则需要设定约束函数和限界函数。在优先队列分支限界法中还有一个关键问题&＃xff0c;即优先级的设定&＃xff1a;选择什么值作为优先级&＃xff1f;如何定义优先级&＃xff1f;因为优先级的设计直接决定算法的效率。