目录

0、前言

1、二阶微分算子的性质

2、二阶微分算子

2.1、Laplacian算子

2.2、LOG算子

0、前言

微分算子其应用着重于图像中的灰度突变区域&＃xff0c;而非灰度级缓慢变化的区域。

之前所介绍的一阶微分算子&＃xff0c;他们的计算都是一次&＃xff0c;左边减去右边一次&＃xff0c;下边减去上边一次&＃xff0c;本节所介绍的是二阶微分算子&＃xff0c;简单来说就是两次计算&＃xff0c;左边减去右边两次&＃xff0c;下边减去上边也是两次。

思路&＃xff1a;

为了能设计出兼顾所有方向的&＃39;&＃39;边缘滤波器&＃39;&＃39;&＃xff0c;就是即使不是360度划分的很密集的方向&＃xff0c;那么至少是在上下垂直对角线上兼顾一下呢&＃xff1f;操作就是使用减中心像素的思想&＃xff0c;就是把四周的信息&＃xff0c;和我们关心的中间点的信息进行对比&＃xff0c;即把上下左右对角线上的和中间都比一下&＃xff0c;把比较的总体结果进行一个中和&＃xff1b;

1、二阶微分算子的性质

 使用二阶微分进行图像锐化&＃xff1b; 

二阶微分&＃xff0c;是一阶微分的导数&＃xff0c;和一阶微分相对应&＃xff0c;二阶微分的性质&＃xff1a;

• &＃xff08;1&＃xff09;在恒定区域二阶微分值为0&＃xff1b;
• &＃xff08;2&＃xff09;在灰度台阶或斜坡的起点处微分值不为0&＃xff1b;
• &＃xff08;3&＃xff09;沿着斜坡的微分值为0&＃xff1b;

2、二阶微分算子

2.1、Laplacian算子

Laplacian算子是二阶的Sobel导数&＃xff0c;在OpenCV中是通过调用Sobel算子来计算Laplacian算子的&＃xff0c;使用的公式和卷积核如下&＃xff1a;

如下计算P5点他的Laplacian算子的梯度&＃xff1a;

88为一个图像中的像素点&＃xff0c;计算该点的梯度值。

  相当于是左边和右边运算两次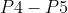&＃xff1a;和 &＃xff08;相当于上下与中间像素操作两次&＃xff09;

上边和下边运算两次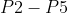&＃xff1a;和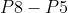

 一阶微分算子每个方向上(X和Y方向)都是运算了一次。(在同一个方向上只运算了一次。)

 而二阶微分算子&＃xff0c;Laplacian算子在X方向上是左边减去中间一次&＃xff0c;右边也减去中间一次&＃xff1b;在Y方向上下边减去中间&＃xff0c;上边也减去中间。(切记操作都是取的绝对值)实际上每个方向上都运算了两次(所以是二阶导数&＃xff0c;不知道这样理解对不对&＃xff1f;意味着在同一个方向上边我进行了两次操作&＃xff0c;都这么直观的理解二阶的由来)

在OpenCV里边不需要我们一步步的去算&＃xff0c;他直接给我们提供了Laplacian这个函数&＃xff1a;

通过调用下边函数就可以对图像进行Laplacian算子的梯度计算&＃xff1a;

实际应用中&＃xff0c;还会有假如对角线方向上的考虑。 

PS&＃xff1a;Laplacian其实就是一个二阶导数&＃xff0c;用来寻找零交叉点的。

2.2、LOG算子

LOG(Laplacian of Gaussian)&＃xff1a;在使用高斯滤波器对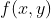滤波(平滑)之后&＃xff0c;通过寻找零交叉来查找边缘。(因为二阶导数对图像是非常敏感的&＃xff0c;所以一般先进行滤波操作&＃xff0c;再进行边缘查找。)

参考链接&＃xff1a;https://www.cnblogs.com/wj-1314/p/9800272.html