本节书摘来自华章计算机《数学建模:基于R》一书中的第2章,第2.4节,作者:薛 毅 更多章节内容可以访问云栖社区“华章计算机”公众号查看。
2.4 数学建模案例分析——气象观察站的优化
2.4.1 问题的提出 该题是1992年西安市大学生数学建模竞赛试题.
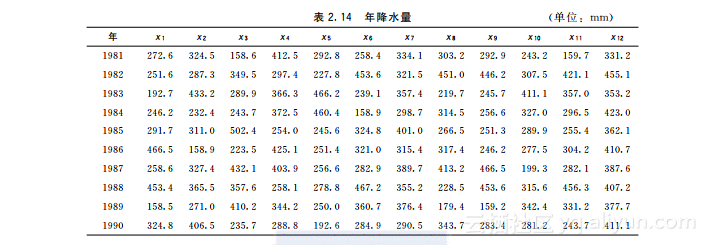
某地区内有12个气象观测站,为了节省开支,计划减少气象观测站的数目.已知该地区12个气象观测站的位置,以及10年来各站测得的年降水量(见表2.14,为便于计算,将表中的数据保存在文本文件rainfall.data中).减少哪些观测站可以使所得到的降水量的信息足够大?观察站分布如图2.7所示.
2.4.2 假设
图2.7 气象观察站分布图1) 相近地域的气象特性具有较大的相似性和相关性,它们之间的影响可以近似为一种线性关系.
2) 该地区的地理特性具有一定的均匀性,而不是表现为复杂多变的地理特性.
3) 在距离较远的条件下,由于地形、环境等因素而造成不同区域的年降水量相似的可能性很小,可以被忽略.不同区域的降水量的差异主要与距离有关.
4) 不考虑其他区域对本地区的影响。
2.4.3 分析
题目要求减少一些观测站,但获得的降水量的信息足够大,如何做到这一点呢?首先要考虑降水量的信息问题.对一个观测站而言,统计10年降水量的均值与方差,均值表示该观测站处降水量的大小,而方差表示降水量变化的大小.粗略地说,如果某观测站测得的降水量的方差为0(这当然是不可能的),则表示该处的降水没有变化,因此,可以用以前的降水量来代替以后的降水量.另一方面,由于相近地域的气象特性具有较大的相似性和相关性,被去掉观测站点的降水量与它附近的观测站点的降水量可以被认为是近似的线性关系.另外,需要对去掉站点的估计值与原观测值进行比较,用以检验估计的效果.因此,得到以下原则
原则1:尽可能去掉降水量方差小的观测站点,用以前的数据来估计这些点的降水量.
原则2:去掉站点的降水量由其他站点降水量的回归方程来估计.
原则3:对去掉站点的观测值与估计值进行比较.
2.4.4 问题的求解
1.计算标准差
求各观测点的标准差,并对标准差由小到大进行排序:X12X7X10X4X2X8
36.8298938.0479457.2472263.9747180.9270585.07349
X11X5X6X1X9X3
86.5135894.1034294.20020100.26600106.40916108.244372. 12号观测站的讨论
按照原则1,首先应该考虑去掉第12号观测站.再按照原则2和12号站点的地理位置,将12号观测站的降水量作为因变量,将8号和11号观测站的降水量作为自变量,作回归方程X12=β8X8+β11X11,通过R软件计算,得到X12=0.6249X8+0.6267X113. 7号观测站的讨论
类似于12号观测站的讨论,作回归方程X7=β3X3+β4X4+β6X6+β8X8+β9X9+β10X10+β11X11利用回归检验和变量选择的方法,将多余变量剔除,发现7号观测站的数据与3号和4号观测站的数据有关,经计算得到回归方程X7=0.50412X3+0.52729X44. 10号观测站的讨论
对于10号站点,经计算得到X10=0.92238X115.结果分析
如果只去掉三个观测站,那么分析到此为止,即去掉12号、7号和10号观测站,它们的信息可由其他观测站的信息作线性组合得到.如果打算继续减少观测站,那么需要作进一步分析.
从标准差的大小来看,应考虑4号观测站,但由于去掉7号观测站需要用4号观测站的信息,因此,只能考虑2号观测站的情况.
对于2号观测站作与10号观测站类似的分析,但不能通过检验,因此,再考虑其他的站点.8号和11号观测站的情况与4号相同,因此,只能讨论5号观测站的情况.
对于5号观测站,经过逐步回归分析,得到回归方程X5=0.8311X9并且通过回归检验,可以去掉5号观测站.
6.计算结果的检验
这里用较为简单的方法对计算结果进行检验,就是画出去掉的观测站点实际的降水量和用其他站点作出的估计值,比较它们之间是否有较大的差异.图2.8给出拟去掉站点的实际降水量和用相关的回归方程得到降水量的预测值,其中实线表示站点的实际降水量,虚线表示用回归方程得到的预测值.
图2.8 拟去掉站点的实际降水量与降水量的预测值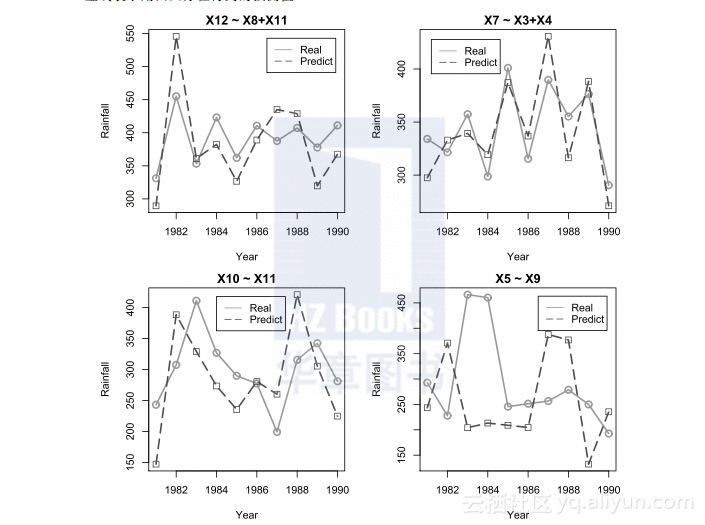
2.4.5 结论
从图2.8中可以看到,12号观测站、7号观测站和10号观测站的预测值与实际值较为接近,但5号观测站的预测值与实际值相差较大,因此,只去掉三个站可能更合理.
习题2
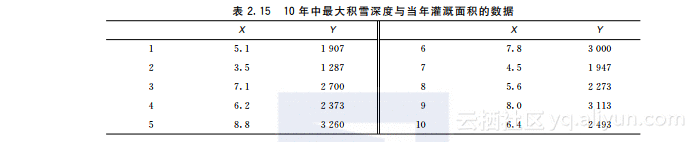
1.为估计山上积雪融化后对下游灌溉的影响,在山上建立一个观测站,测量最大积雪深度X(米)与当年灌溉面积Y(公顷),测得连续10年的数据如表2.15所示.(1)建立一元线性回归模型、求解,并验证系数、方程或相关系数是否通过检验;(2)现测得今年的数据是X=7米,给出今年灌溉面积的预测值、预测区间和置信区间(α=0.05).
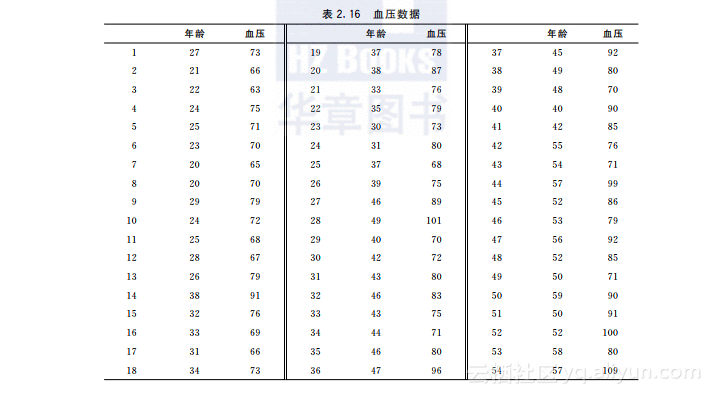
2.现测得20~60岁成年女性的血压(见表2.16),分析血压与年龄之间的回归关系,并作残差分析.检验残差是否满足正态性、方差齐性的要求.如果不满足方差齐性要求,请作Box-Cox变换,再作回归分析.试分析,作了Box-Cox变换后,残差是否满足方差齐性要求.
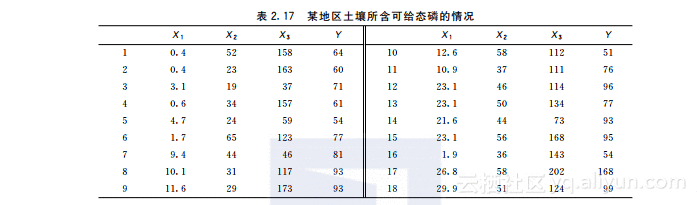
3.研究同一地区土壤所含可给态磷(Y)的情况,得到18组数据如表2.17所示.表中X1为土壤内所含无机磷浓度,X2为土壤内溶于K2CO3溶液并受溴化物水解的有机磷,X3为土壤内溶于K2CO3溶液但不溶于溴化物水解的有机磷.(1)建立多元线性回归方程模型,求解,并验证系数、方程或相关系数是否通过检验;(2)作逐步回归分析.
4.进行一次试验,当缓慢旋转的布面轮子受到磨损时,比较三种布上涂料的磨损量.对每种涂料类型试验10个涂料样品,记录每个样品直到出现可见磨损时的小时数,数据在表2.18中给出.试用单因素方差分析方法分析:这三种涂料直至磨损明显可见的平均时间是否存在显著差异?如果存在,请作多重t检验,分析哪种涂料之间存在显著差异.

5.使用方差不同模型(如oneway.test()函数)和秩检验方法(如kruskal.test()函数)对第4题中的数据进行分析,是否得到与第4题相同的结果?如果得到的结论不同,哪个结论更合理,试对数据作正态性检验(如shapiro.test()函数)和方差齐性检验(如bartlett.test()函数)来说明这一问题.
6.清洁金属部件有三种有机溶剂:芬芳剂、氯烷和酯类,表2.19给出了这三种溶剂吸附比的测试结果,能否根据这组数据分析出这三种溶剂的吸附比存在差显著差异?如果存在,请作多重t检验,分析哪种有机溶剂之间存在显著差异.

77.对第6题中的数据进行正态性检验和方差齐性检验,试分析:使用方差不同模型(如oneway.test()函数)和方差相同模型(如aov()函数)哪个更合理?
8.考查不同职业人群对心理疾病原因的认识,现找到A,B,C三种职业的人员各10名,这30个人用笔试的方式回答心理疾病原因的知识问卷,测试分数如表2.20所示.(1)使用Kruskal-Wallis秩和检验,分析这三种职业人员平均测试分数是否有显著差异?(2)使用正态性检验和方差齐性检验的方法来分析Kruskal-Wallis秩和检验的合理性.

9.表2.21给出某种化工过程在三种浓度、四种温度下得率的数据.(1)对数据作方差分析(考虑有交互作用的情况);(2)计算各种温度下得率均值的估计,各种浓度下得率均值的估计,以及同时考虑温度和浓度下得率均值的估计;(3)通过(1)与(2)计算结果来说明,在今后的生产中,我们将如何选择生产的温度和浓度,使得这些条件对生产最有利(注意,一定要说明理由).

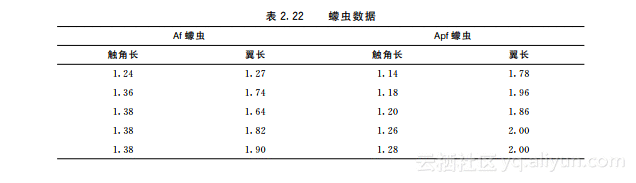
10.两种蠓虫Af和Apf已由生物学家Grogan和Wirth(1981年)根据它们的触角长度和翼长加以区分,现已知9只Af蠓虫和6只Apf蠓虫,数据如表2.22所示.试用线性判别函数(lda()函数)和二次判别函数(qda()函数)判断给定的蠓虫属于哪一族?将这两种方法用于触角长和翼长分别为(1.24,1.80),(1.28,1.84),(1.40,2.04)的三个标本.并分析两种方法的计算结果哪一个更可靠.
562.08
11.某医院研究心电图指标对健康人(Ⅰ)、硬化症患者(Ⅱ)和冠心病患者(Ⅲ)的鉴别能力.现获得训练样本如表2.23所示.试用R中的判别函数对数据进行分析(取先验概率为11/23,7/23,5/23,随机地选择2,1,1个样本分别作为三类样本的待测样本,余下的样本作为训练样本).