0. 引言
完成了SLAM14讲的学习,来VIO进行进阶。
1. 概述与课程介绍
Section1. 课程介绍



Section2. VIO概述

为什么把视觉和IMU结合在一起?
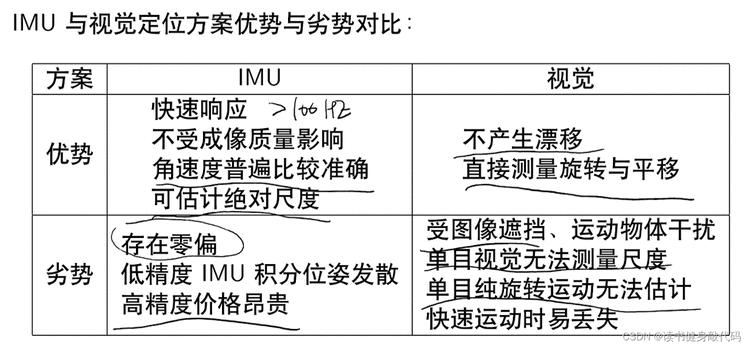
因为这两个sensor是互补的,视觉测慢的,IMU测快的;视觉漂移小,IMU有漂移。
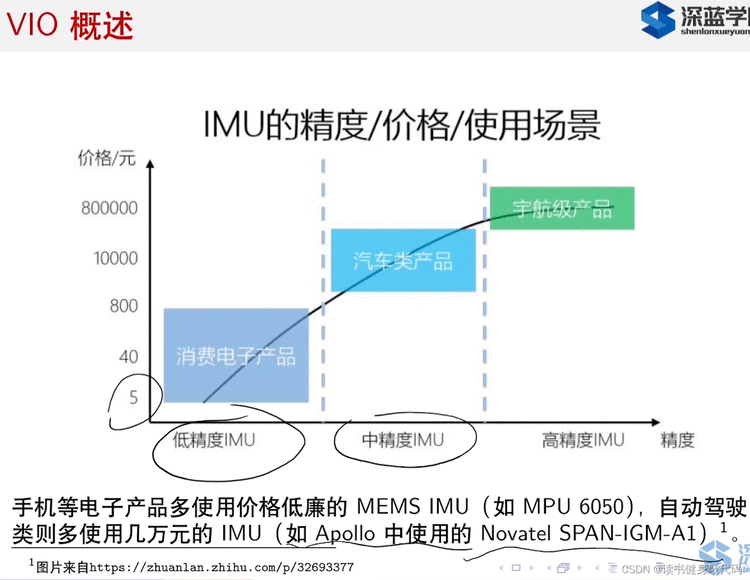
说VIO要明确是跟什么层次的IMU进行融合,各种层次的IMU的角速度普遍比较准确,但便宜的IMU加速度计精度差,基本上只能看个方向,贵的好的可以直接通过积分得到位姿。在飞机上用的很好的IMU,同样的算法在手机上可能就没那么好了。
手机的IMU可能几s就飞了,汽车级别的IMU可能估计个30s就飞了(在GPS,Lidar等失效的情况下)
VIO是在工业界用的较多的一种方案,主要在AR/VR, Robotic/无人机(drone),等,这些场景Lidar的功耗太高,不适合使用,比如VR眼镜,装个IMU是可以的。
而且在场景中要分清楚到底是基于地图的定位还是基于odometer的定位。基于odometer的定位是只要知道他的相对运动,而如果需要知道相对于真实物理世界的运动,则需要建图等,在地图中定位。
需要指出,相对运动无论多准都会有累积误差(VIO是估计相对位姿的),即使VIO很准还是会飘,就变成原来15s不能用,现在30s不能用的东西了。如果是基于地图定位就不用太过纠结odometry,AR/VR需要快速地知道短时间内物体的运动,VIO可用,手机防抖

视觉可以纠正IMU的零偏,IMU可以为视觉提供尺度信息,或者在视觉丢失的时候顶上去。
VIO可分为松耦合和紧耦合。
-
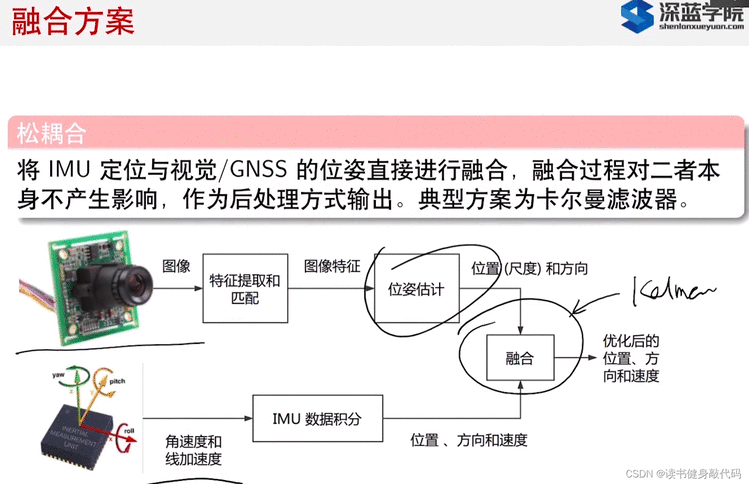
松耦合: IMU和视觉自己算自己的,通过后处理的方法将两个结果融合(典型融合方法是Kalman滤波)。(因为后处理不会影响前面的结果,所以二者是相互独立的。)
-
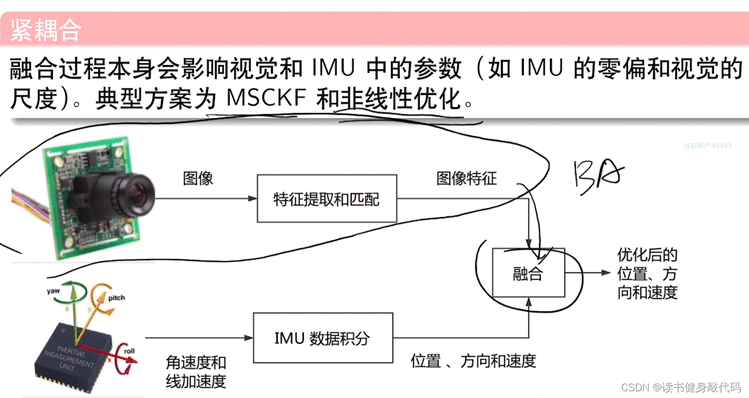
紧耦合:IMU和视觉相互弥补。(视觉可能是一个BA,IMU是一组运动方程 )课程主要介绍紧耦合。

GPS,RTK受场景约束,有些场景很好用,有些场景就不行。

Section 3. 预备知识回顾



默认以
T
w
i
Twi
Twi表示IMU的定位信息,平移可以直接看作IMU在world中的坐标。


由四元数的叉乘可得,一个四元数
q
q
q等于自身与
[
0
,
1
]
T
[0, \boldsymbol 1]^T
[0,1]T做叉乘。
四元数求导:
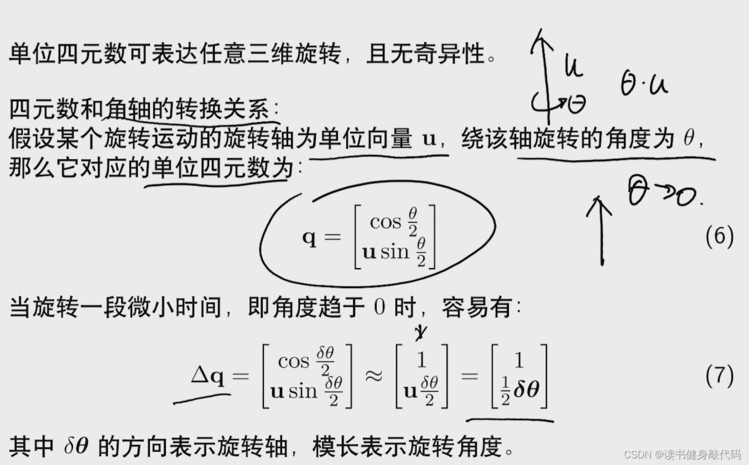
对cos和sin进行泰勒展开即得四元数的变化量。
两个四元数叉乘就代表把右边的四元数按照左边的旋转转了一下。
参考:

δ
θ
\delta \theta
δθ当
△
t
△t
△t趋近于0时即为角速度
ω
\omega
ω
当使用旋转矩阵表示旋转时(和四元数没有本质上的区别),导数可以用泊松公式表示:
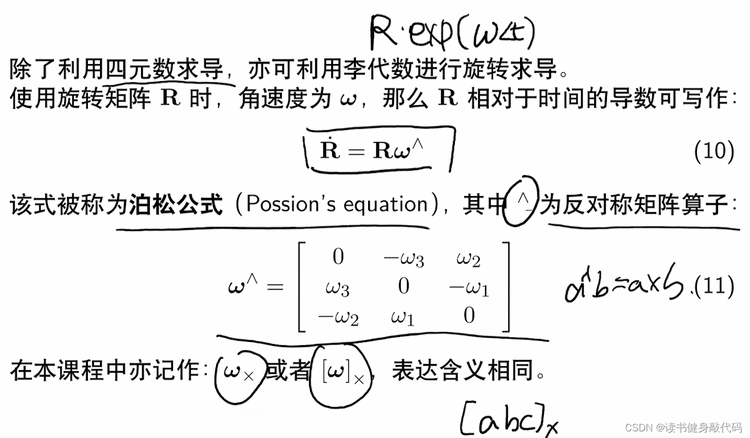
因为
a
∧
b
=
a
×
b
a ^\wedge b=a \times b
a∧b=a×b,所以也可以写成
ω
×
\boldsymbol \omega_{\times}
ω×
左乘时
∂
R
p
∂
ϕ
=
−
(
R
p
)
∧
\frac{\partial Rp}{\partial \phi}=-(Rp)^\wedge
∂ϕ∂Rp=−(Rp)∧,右乘是
−
R
p
∧
-Rp^\wedge
−Rp∧
导数算出来后,如果是按照左扰动模型求的,就左乘更新上去,右扰动就右乘更新上去。
SO(3)导数,比如对旋转的导数

本课程习惯使用右乘