深度学习三人行(第3期)TensorFlow从DNN入手

我们已经学习了TensorFlow的一些基础知识&＃xff0c;

深度学习三人行(第1期)---- TensorFlow爱之初体验

深度学习三人行(第2期)---- TensorFlow爱之再体验

该期我们将从DNN入手开始学习TensorFlow方面的相关知识。学习的路上&＃xff0c;我们多多交流&＃xff0c;共同进步。本期主要内容如下&＃xff1a;

• 从生物学到人工神经网络

• 训练多层感知机

• 训练DNN

文末附本期代码关键字&＃xff0c;回复关键字即可下载。

一. 从生物学到人工神经网络

鸟类启发我们飞翔&＃xff0c;牛蒡植物启发魔术贴&＃xff0c;而大自然激发了许多其他发明。 那么&＃xff0c;大脑的体系结构&＃xff0c;是激发人工神经网络&＃xff08;ANN&＃xff09;的关键思想。人工神经网络是深度学习的核心。

1.1 从生物到人工神经元

在讨论人造神经元之前&＃xff0c;让我们快速看一下生物神经元&＃xff0c;如下图所示。它是一种看起来很奇特的细胞&＃xff0c;主要存在于动物大脑皮层&＃xff08;例如&＃xff0c;你的大脑&＃xff09;中&＃xff0c;由含有细胞核和大部分细胞复杂成分的细胞体以及许多称为树突的分支延伸部分组成&＃xff0c;还有一个非常长的延伸部分&＃xff0c;称为轴突。轴突的长度可能比细胞体长几倍&＃xff0c;或长达几万倍。靠近其末端的轴突分裂出成许多分支称为终树突&＃xff0c;并且在这些分支的尖端是微小的结构&＃xff0c;称为突触末端&＃xff08;或简称突触&＃xff09;&＃xff0c;其被连接到树突&＃xff08;或直接到细胞体&＃xff09;的其他神经元。生物神经元通过这些突触接收来自其他神经元的信号的短电脉冲。当一个神经元在几毫秒内接收到来自其他神经元的足够数量的信号时&＃xff0c;它会触发自己的信号。

tf.assign()函数的作用是创建一个将新值赋给变量的一个节点&＃xff0c;这里相当于执行如下迭代&＃xff1a;

因此&＃xff0c;单个生物神经似乎表现得相当简单&＃xff0c;但它们组织在一个数十亿个神经元的庞大网络中&＃xff0c;每个神经元通常与数千个其他神经元相连时情况就不同了。生物神经网络&＃xff08;BNN&＃xff09;的体系结构仍然是积极研究的主题&＃xff0c;大脑的某些部分结构已经被打印出来&＃xff0c;似乎神经元通常以连续的层次组织&＃xff0c;如下图所示。

二. 训练多层感知机

Warren McCulloch和Walter Pitts提出了一个非常简单的生物神经元模型&＃xff0c;该模型后来被称为人造神经元&＃xff1a;它具有一个或多个二进制&＃xff08;开/关&＃xff09;输入和一个二进制输出。 当超过一定数量的输入有效时&＃xff0c;人造神经元会简单地激活其输出。 McCulloch和Pitts表明&＃xff0c;有了这样一个简化的模型&＃xff0c;我们可以建立一个人造神经元网络&＃xff0c;计算你想要的任何逻辑命题。 例如&＃xff0c;假设神经元至少有两个输入有效时激活神经元&＃xff0c;就可以构建一些执行各种逻辑运算的ANN&＃xff0c;如下图所示。

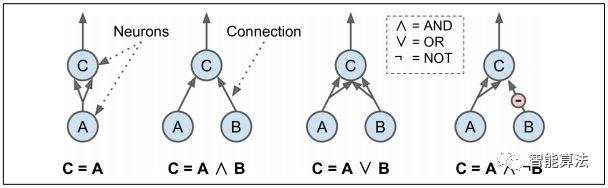
感知机是Frank Rosenblatt于1957年发明的最简单的ANN架构之一。 它基于一个稍微不同的人造神经元&＃xff08;见下图&＃xff09;&＃xff0c;称为线性阈值单元&＃xff08;LTU&＃xff09;&＃xff1a;输入和输出现在是数字&＃xff08;而不是二进制开/关值&＃xff09;&＃xff0c;每个输入连接都与一个重量。 LTU计算其输入的加权和(z &＃61; w1 x1 &＃43; w2 x2 &＃43; ⋯ &＃43; wn xn &＃61; wT · x)&＃xff0c;然后对该和应用阶跃函数并输出结果&＃xff1a;hw&＃xff08;x&＃xff09;&＃61; step&＃xff08;z&＃xff09; &＃61; step&＃xff08;wT·x&＃xff09;。

在感知机中使用的最常用的是Heaviside阶跃函数&＃xff08;见如下公式&＃xff09;。 有时使用符号函数代替。

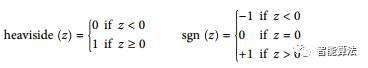
单层感知器仅由单层LTU组成&＃xff0c;每个神经元连接到所有输入&＃xff0c;通常会添加一个额外的偏差特征&＃xff08;x0 &＃61; 1&＃xff09;。具有两个输入和三个输出的感知器如下图所示。 这个感知器可以将实例同时分为三个不同的二进制类&＃xff0c;这使得它成为一个多输出分类器。

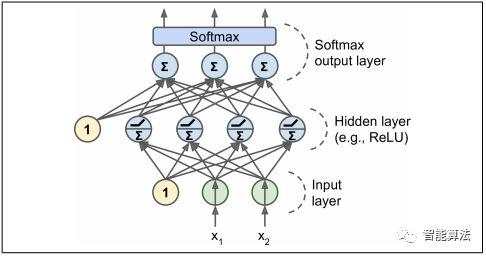
一个MLP由一个&＃xff08;直通&＃xff09;输入层&＃xff0c;一个或多个LTU层组成&＃xff0c;称为隐藏层&＃xff0c;最后一层LTU称为输出层&＃xff08;如下图所示&＃xff09;。 除输出层以外的每一层都包含一个偏置神经元&＃xff0c;并完全连接到下一层。 当ANN具有两个或更多个隐藏层时&＃xff0c;它被称为深度神经网络&＃xff08;DNN&＃xff09;。

多年来&＃xff0c;研究人员一直在努力寻找一种培训MLP的方法&＃xff0c;但没有成功。但在1986年&＃xff0c;D. E. Rumelhart 等人。发表了一篇突破性文章&＃xff0c;介绍反向传播训练算法。对于每个训练实例&＃xff0c;算法将其输入到网络并计算每个神经元的输出&＃xff08;这是正向传递&＃xff0c;就像进行预测时一样&＃xff09;。 然后它计算网络的输出误差&＃xff08;即期望的输出和网络的实际输出之间的差异&＃xff09;&＃xff0c;并且它计算最后一个隐藏层中的每个神经元对每个输出神经元的误差有多大贡献。然后继续测量这些误差贡献中多少来自前一个隐藏层中的每个神经元 - 等等直到算法到达输入层。

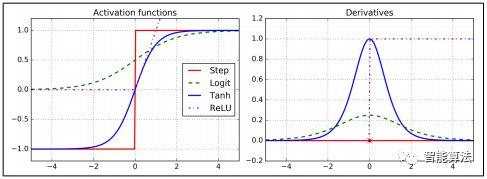
为了使这个算法正常工作&＃xff0c;作者对MLP的架构做了一个关键的改变&＃xff1a;他们用logistic函数σ&＃xff08;z&＃xff09;&＃61; 1 /&＃xff08;1 &＃43; exp&＃xff08;-z&＃xff09;&＃xff09;代替了阶跃函数。 这是很重要的&＃xff0c;因为阶跃函数只包含平坦段&＃xff0c;所以没有梯度可用&＃xff08;梯度下降不能在平坦表面上移动&＃xff09;&＃xff0c;而logistic函数在每个地方都有一个定义明确的非零导数&＃xff0c;允许渐变下降 每一步都有进步。 反向传播算法可以与其他激活函数一起使用&＃xff0c;而不是逻辑函数。 其他两种流行的激活功能是&＃xff1a;

1.双曲正切函数tanh&＃xff08;z&＃xff09;&＃61;2σ&＃xff08;2z&＃xff09; - 1

它是S形的&＃xff0c;连续的&＃xff0c;可微分的&＃xff0c;但是它的输出值范围从-1到1&＃xff08;而不是在逻辑函数中为0到1&＃xff09;&＃xff0c;这往往会使每一层的输出更大或训练开始时标准化程度较低&＃xff08;即以0为中心&＃xff09;。

2.ReLU功能

ReLU&＃xff08;z&＃xff09;&＃61; max&＃xff08;0&＃xff0c;z&＃xff09;。 它是连续的&＃xff0c;但不幸的是它在z &＃61; 0时不可微分&＃xff08;斜率突然变化&＃xff0c;这可能导致梯度下降反弹&＃xff09;。实际上它运行得非常好&＃xff0c;并且具有快速计算的优点。

这些流行的激活函数及其衍生物如图下图所示。

MLP通常用于分类&＃xff0c;每个输出对应于不同的二进制类&＃xff08;例如&＃xff0c;垃圾邮件/火腿&＃xff0c;紧急/不紧急等等&＃xff09;。当这些类是排他性的&＃xff08;例如&＃xff0c;数字图像分类的类0到9&＃xff09;时&＃xff0c;输出层通常通过用共享的softmax函数代替单独的激活函数&＃xff08;见下图&＃xff09;。 softmax函数在机器学习系列中介绍过。每个神经元的输出对应于相应类的估计概率。 请注意&＃xff0c;信号仅在一个方向上&＃xff08;从输入到输出&＃xff09;流动&＃xff0c;所以此架构是前馈神经网络&＃xff08;FNN&＃xff09;的一个示例。

使用TensorFlow训练MLP的最简单方法是使用高级API TF.Learn&＃xff0c;它与Scikit-Learn的API非常相似。 DNNClassifier类使得使用任意数量的隐藏层训练深层神经网络和softmax输出层来输出估计类别概率变得十分简单。 例如&＃xff0c;下面的代码训练一个DNN用于分类两个隐藏层&＃xff08;一个具有300个神经元&＃xff0c;另一个具有100个神经元&＃xff09;以及一个具有10个神经元的softmax输出层&＃xff1a;

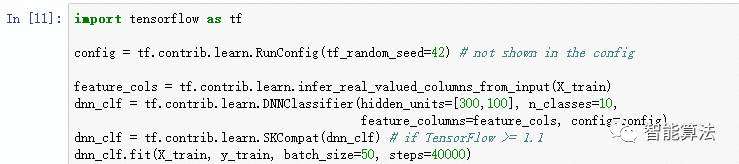
如果您在MNIST数据集上运行此代码&＃xff08;在对其进行缩放后&＃xff08;例如&＃xff0c;通过使用ScikitLearn的StandardScaler&＃xff09;&＃xff0c;您可能会得到一个在测试集上的准确率超过98.2&＃xff05;的模型&＃xff01; 这比我们在机器学习系列文章的模型中训练的最佳模型要好&＃xff1a;

代码过长&＃xff0c;详细代码请移步公众号“智能算法”回复文末关键字下载。

三. 训练DNN

这里我们将实现Minibatch渐变下降以在MNIST数据集上进行训练。 第一步是构建阶段&＃xff0c;构建TensorFlow图。 第二步是执行阶段&＃xff0c;您可以在其中实际运行图来训练模型。

3.1 构建阶段

首先&＃xff0c;我们需要导入tensorflow库。 然后&＃xff0c;我们必须指定输入和输出的数量&＃xff0c;并设置每层中隐藏的神经元的数量&＃xff1a;

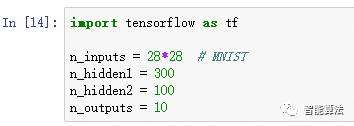
接下来&＃xff0c;我们可以使用占位符节点来表示训练数据和目标。 X的形状只是部分定义的。 我们知道它将是一个二维张量&＃xff08;即矩阵&＃xff09;&＃xff0c;沿第一维的实例和沿第二维的特征&＃xff0c;并且我们知道特征的数量将是28 x 28&＃xff08;每像素一个特征&＃xff09; &＃xff0c;但我们还不知道每个培训批次将包含多少个实例。 所以X的形状是&＃xff08;None&＃xff0c;n_inputs&＃xff09;。 同样&＃xff0c;我们知道y将是每个实例有一个入口的一维张量&＃xff0c;但是在这一点上我们也不知道训练批量的大小&＃xff0c;因此形状是&＃xff08;无&＃xff09;。

现在我们来创建实际的神经网络。 占位符X将充当输入层; 在执行阶段&＃xff0c;它将一次替换为一个训练批次&＃xff08;请注意&＃xff0c;训练批次中的所有实例都将由神经网络同时处理&＃xff09;。 现在你需要创建两个隐藏层和输出层。 这两个隐藏层几乎是相同的&＃xff1a;它们的区别仅在于它们所连接的输入以及它们包含的神经元的数量。 输出层也非常相似&＃xff0c;但它使用softmax激活功能而不是ReLU激活功能。 因此&＃xff0c;让我们创建一个我们将用来一次创建一个图层的neuron_layer&＃xff08;&＃xff09;函数。 它将需要参数来指定输入&＃xff0c;神经元的数量&＃xff0c;激活函数和图层的名称&＃xff1a;

让我们一行一行地看看这段代码&＃xff1a;

1.首先我们使用图层的名称创建一个名称范围&＃xff1a;它将包含该神经元图层的所有计算节点。 这是可选的&＃xff0c;但如果TensorBoard中的节点组织良好&＃xff0c;该图形在TensorBoard中看起来会更好。

2.接下来&＃xff0c;我们通过查询输入矩阵的形状并获得第二维的大小&＃xff08;第一维是实例&＃xff09;来获得输入的数量。

3.接下来的三行创建一个W变量&＃xff0c;它将保存权重矩阵。 它将是一个二维张量&＃xff0c;其中包含每个输入和每个神经元之间的所有连接权重; 因此&＃xff0c;它的形状将是&＃xff08;n_inputs&＃xff0c;n_neurons&＃xff09;。 它将被随机初始化&＃xff0c;使用标准偏差为2 / ninputs的截断法线&＃xff08;高斯&＃xff09;分布。 使用这个特定的标准偏差有助于算法更快地收敛。 为所有隐藏层随机初始化连接权重非常重要&＃xff0c;以避免梯度下降算法无法打破的任何对称性。

4.下一行为偏差创建一个b变量&＃xff0c;初始化为0&＃xff08;在这种情况下不存在对称性问题&＃xff09;&＃xff0c;每个神经元具有一个偏置参数。

5.然后我们创建一个子图来计算z &＃61; X·W &＃43; b。 这种向量化的实现将有效地计算输入的加权和加上层中每个神经元的偏置项&＃xff0c;对于批处理中的所有实例&＃xff0c;只需一次。

6.最后&＃xff0c;如果激活参数设置为“relu”&＃xff0c;则代码返回relu&＃xff08;z&＃xff09;&＃xff08;即&＃xff0c;max&＃xff08;0&＃xff0c;z&＃xff09;&＃xff09;&＃xff0c;否则它只返回z。

好的&＃xff0c;现在你有一个很好的功能来创建一个神经元层。 让我们用它来创建深度神经网络&＃xff01; 第一个隐藏层将X作为输入。 第二个将第一个隐藏层的输出作为输入。 最后&＃xff0c;输出层将第二个隐藏层的输出作为输入。

请注意&＃xff0c;为了清晰起见&＃xff0c;我们再次使用名称范围。 还要注意&＃xff0c;在通过softmax激活函数之前&＃xff0c;logits是神经网络的输出&＃xff1a;出于优化原因&＃xff0c;我们稍后将处理softmax计算。

正如你所期望的那样&＃xff0c;TensorFlow具有许多方便的功能来创建标准的神经网络图层&＃xff0c;所以通常不需要像我们刚才那样定义自己的神经元层&＃xff08;&＃xff09;函数。 例如&＃xff0c;TensorFlow的dense&＃xff08;&＃xff09;函数创建一个完全连接的层&＃xff0c;其中所有输入连接到该层中的所有神经元。 只需导入该函数并用以下代码替换dnn构造部分&＃xff1a;

现在我们已经准备好了神经网络模型&＃xff0c;我们需要定义我们将用来训练它的代价函数。我们将使用交叉熵&＃xff0c;交叉熵会惩罚估计目标类别的概率较低的模型。 TensorFlow提供了几个函数来计算交叉熵。 我们将使用sparse_softmax_cross_entropy_with_logits&＃xff08;&＃xff09;。 这将给我们一个包含每个实例的交叉熵的一维张量。然后&＃xff0c;我们可以使用TensorFlow的reduce_mean&＃xff08;&＃xff09;函数来计算所有实例的平均交叉熵。

我们有神经网络模型&＃xff0c;我们有代价函数&＃xff0c;现在我们需要定义一个GradientDescentOptimizer来调整模型参数以最小化代价函数&＃xff1a;

构造阶段的最后一个重要步骤是指定如何评估模型。我们可以使用in_top_k&＃xff08;&＃xff09;函数。 这将返回一个布尔值为1D的张量&＃xff0c;所以我们需要将这些布尔值转换为浮点数&＃xff0c;然后计算平均值。 这会给我们网络的整体准确性。

我们需要创建一个节点来初始化所有变量&＃xff0c;并且我们还将创建一个Saver以将我们训练好的模型参数保存到磁盘&＃xff1a;

3.2 构建阶段

这部分更短&＃xff0c;更简单。 首先&＃xff0c;我们加载MNIST。 我们可以使用ScikitLearn&＃xff0c;但TensorFlow提供了自己的帮助程序&＃xff0c;它可以提取数据&＃xff0c;对数据进行缩放&＃xff08;0到1之间&＃xff09;&＃xff0c;对其进行混洗&＃xff0c;并提供一个简单的函数来一次加载一个小批量。 所以让我们用它来执行&＃xff1a;

此代码打开TensorFlow会话&＃xff0c;并运行初始化所有变量的init节点。 然后它运行主要的训练循环&＃xff1a;在每个时代&＃xff0c;代码迭代对应于训练集大小的许多小批量。 每个小批量都通过next_batch&＃xff08;&＃xff09;方法获取&＃xff0c;然后代码简单地运行训练操作&＃xff0c;为其提供当前的最小批量输入数据和目标。 接下来&＃xff0c;在每个迭代结束时&＃xff0c;代码将在最后一个小批量和完整训练集上评估模型&＃xff0c;并打印出结果。 最后&＃xff0c;模型参数保存到磁盘。

3.3 使用神经网络

现在神经网络已经过训练&＃xff0c;您可以使用它来进行预测。 要做到这一点&＃xff0c;你可以重复使用相同的构造阶段&＃xff0c;但像这样改变执行阶段&＃xff1a;

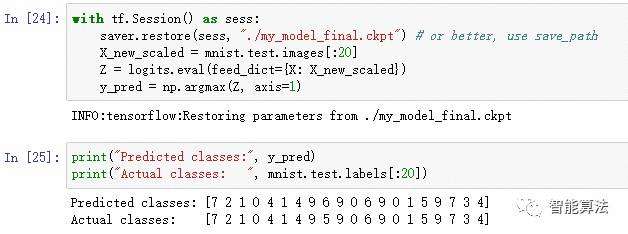
首先代码从磁盘加载模型参数。 然后它加载一些你想分类的新图像。然后代码评估logits节点。 如果你想知道所有估计的类概率&＃xff0c;你需要将softmax&＃xff08;&＃xff09;函数应用于logits&＃xff0c;但是如果你只是想预测一个类&＃xff0c;你可以简单地选择具有最高logit值的类&＃xff08;使用 argmax&＃xff08;&＃xff09;函数执行这个技巧&＃xff09;。

四. 本期小结

至此&＃xff0c;我们了解了神经网络的由来&＃xff0c;并且训练了多层感知机以及DNN神经网络。

&＃xff08;如需更好的了解相关知识&＃xff0c;欢迎加入智能算法社区&＃xff0c;在“智能算法”公众号发送“社区”&＃xff0c;即可加入算法微信群和QQ群&＃xff09;

本文代码回复关键字&＃xff1a;tfdnn