小侠客们周末愉快呀,又到了每周的学习时间,我是oubahe。今天我们探讨一下如何使用深度学习模型做到对目标值的区间预测。使用神经网络做回归任务,我们使用MSE、MAE作为损失函数,最终得到的输出y通常会被近似为y的期望值,例如有两个样本:(x=1, y=3)和(x=1, y=2),那只用这两个样本训练模型,预测x=1时y的值就是2.5。但有些情况下目标值y的空间可能会比较大,只预测一个期望值并不能帮助我们做进一步的决策。我们想知道x=1时,y的值最小会是多少,最大会是多少,使用MSE、MAE这些损失函数来构建预测输出区间模型时候,往往需要对样本进行非常复杂的处理才能达到目的,而且因为数据的预处理需要加入很强的先验信息,建模效果肯定会打折扣,再一个如果数据规模比较大,那将会在数据预处理上浪费大量的时间。来吧,展示~
01
引言
这里介绍一个特殊的损失函数——分位数损失,利用分位数损失我们不需要对数据进行任何先验的处理,就可以轻松做到预测输出y的某一分位数水平值,例如5%分位数或95%分位数,利用这个输出很自然就完成预测输出范围的回归模型。分位数损失函数的表达式如下: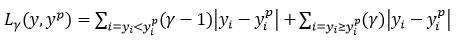
其中,γ是损失函数的参数,从实际意义上可以理解为是我们需要的分位数,这个损失函数从结构上看,就是以一定的概率γ惩罚预测值大于实际值,同时鼓励预测值小于实际值,这样的效果就是学得了目标y的γ分位数期望值。对于分位数损失函数的具体应用可以参考下边的例子。
02
分位数损失函数
我们这里以波士顿房价数据集为例理解一下分位数损失函数的效果。首先加载数据并进行分割,另外为了可视化方便,我们将x_test进行PCA降维并排序:
boston_data = load_boston()
x = boston_data['data']
y = boston_data['target']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=77)
# PCA对数据进行降维处理,方便可视化
pca = PCA(n_compOnents=1)
x_test_after_pca = pca.fit_transform(x_test, y_test)
# 对数据进行排序
x_sort_id = np.argsort(x_test, axis=None)
x_test = x_test[x_sort_id]
y_test = y_test[x_sort_id]
x_for_visual = x_test_after_pca[x_sort_id]
第二步就是损失函数的定义,在Tensorflow2.0中没有分位数函数的定义,可以根据公式来进行定义:def quantile_loss(y_pred, y_true, r=0.5):
greater_mask = K.cast((y_true <= y_pred), 'float32')
smaller_mask = K.cast((y_true > y_pred), 'float32')
return K.sum((r-1)*K.abs(smaller_mask*(y_true-y_pred)), -1)+K.sum(r*K.abs(greater_mask*(y_true-y_pred)), -1)
在这里,我们给出一种更简洁的定义方式:
def tilted_loss(q, y_true, y_pred):
e = (y_true-y_pred)
return K.mean(K.maximum(q*e, (q-1)*e), axis=-1)
进一步地,我们构建一个最简单的模型:
def gen_model(ipt_dim):
l1 = Input(shape=(ipt_dim,))
l2 = Dense(10, activation='relu', kernel_initializer=glorot_normal(), bias_initializer=zeros())(l1)
l3 = Dense(5, activation='relu', kernel_initializer=glorot_normal(), bias_initializer=zeros())(l2)
l4 = Dense(1, activation='relu', kernel_initializer=glorot_normal(), bias_initializer=zeros())(l3)
m_model = Model(inputs=l1, outputs=l4)
return m_model
plt.figure()
plt.scatter(x_for_visual, y_test, label='actual')
q_list = [0.1, 0.5, 0.9]
for quantile in q_list:
model = gen_model(in_dims)
model.compile(loss=lambda y_t, y_p: tilted_loss(quantile, y_t, y_p), optimizer='adam')
model.fit(x_train, y_train, epochs=5, batch_size=8, verbose=1)
y_ = model.predict(x_test)
plt.plot(x_for_visual, y_, label=quantile)
plt.legend()
plt.show()
可视化的最终结果如下图所示,我们可以看到学习到的三个档位的分位数回归模型。其中0.5的与普通MAE回归结果是等价的,只不过0.5预测的是中位数而MAE预测的是期望值;0.1和0.9的两条曲线可以作为预测结果的上下界,能够包含其中80%的数据结果,如果我们追求更高的区间置信度,可以选择更低的下界分位数和更高的上界分位数。03
总结
以上就是深度学习分位数回归实现区间预测的所有内容了,一般来说,大家在深度回归模型中分别使用1/4中位数和3/4中位数作为上下界分位数损失函数,得到的上下界分位数回归结果是具有95%置信度的。
在回归任务中,我们可以轻松构建能够预测输出值范围的模型,并且不依赖对数据的先验处理,是一种非常高效的方法;另外分位数损失函数的实现,推荐使用文中的第二种方法,涉及的计算步骤更少,效率更高;分位数损失函数与MAE损失类似,是一种线性的损失函数,在loss在0附近的区间内同样存在导数不连续的问题,各位聪明的小侠客如果能有简单的方法可以规避这个缺点,则会更加好用。好啦,今天的内容就到这里啦,我是oubahe,我们下次再见咯~码字虽少,原创不易。分享是快乐的源泉,来个素质三连 —>点击左下角分享 —> 右下角点赞+在看本文,可以汇聚好运气召唤神龙哟~