沙漏结构中的最大总和值分析

给你一个大小为 m x n 的整数矩阵 grid 。

按以下形式将矩阵的一部分定义为一个 沙漏 ：

返回沙漏中元素的 最大 总和。

注意：沙漏无法旋转且必须整个包含在矩阵中。

示例 1：

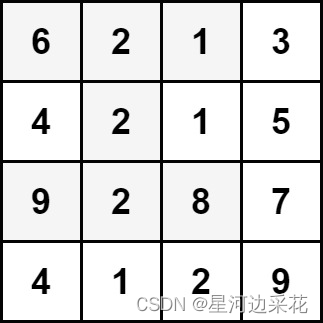
输入：grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]]
输出：30
解释：上图中的单元格表示元素总和最大的沙漏：6 + 2 + 1 + 2 + 9 + 2 + 8 = 30 。

示例 2：

输入：grid = [[1,2,3],[4,5,6],[7,8,9]]
输出：35
解释：上图中的单元格表示元素总和最大的沙漏：1 + 2 + 3 + 5 + 7 + 8 + 9 = 35 。

提示：

    m == grid.length
    n == grid[i].length
    3 <= m, n <= 150
    0 <= grid[i][j] <= 106

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-sum-of-an-hourglass
 

思路：

枚举每一个沙漏，但是我们可以用前缀和计算一个3*3正方形然后剪掉那两块。

AC代码：

class Solution {
public:
#define N 155
typedef long long LL;
LL a[N][N],s[N][N];int maxSum(vector>& g) {int n = g.size();int m = g[0].size();for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){a[i][j]=g[i-1][j-1];s[i][j]=a[i][j]+s[i-1][j]+s[i][j-1]-s[i-1][j-1];}LL res=0;for(int i=3;i<=n;i++)for(int j=3;j<=m;j++){int x1=i-2;int y1=j-2;LL sum = s[i][j]-s[x1-1][j]-s[i][y1-1]+s[x1-1][y1-1];sum=sum-a[i-1][j]-a[i-1][j-2];res = max(sum,res);}return res;}
};