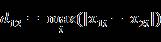请比较欧式距离与曼哈顿距离？

1. 欧氏距离(Euclidean Distance)

欧氏距离是最容易直观理解的距离度量方法，我们小学、初中和高中接触到的两个点在空间中的距离一般都是指欧氏距离。

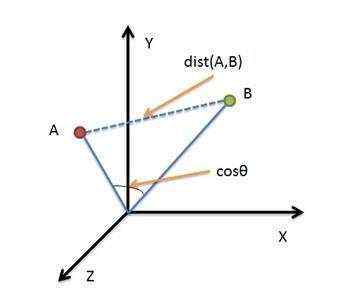
• 二维平面上点a(x1,y1)与b(x2,y2)间的欧氏距离:

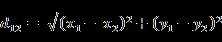
• 三维空间点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:

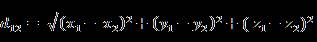
• n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的欧氏距离（两个n维向量）：

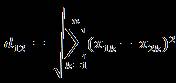
2. 曼哈顿距离(Manhattan Distance)

顾名思义，在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。

• 二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离：

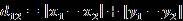
• n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离：

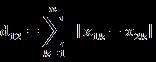
3. 切比雪夫距离 (Chebyshev Distance)

国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。

• 二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离：

• n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的切比雪夫距离：