MySQL的索引是如何实现的

分享一个大牛的人工智能教程。零基础&＃xff01;通俗易懂&＃xff01;风趣幽默&＃xff01;希望你也加入到人工智能的队伍中来&＃xff01;请点击http://www.captainbed.net

mysql中索引分三类&＃xff1a;B&＃43;树索引、Hash索引、全文索引。InnoDB存储引擎中用的是B&＃43;树索引。要介绍B&＃43;树索引&＃xff0c;不得不提二叉查找树、平衡二叉树和B树这三种数据结构。B&＃43;树是从它们三个演化来的。

二叉查找树&＃xff1a;

图中为user表建立了一个二叉查找树的索引。节点中存储了键&＃xff08;key&＃xff09;和数据&＃xff08;data&＃xff09;。数据对应user表中的行数据。

如果查找id&＃61;12的用户信息&＃xff0c;流程如下&＃xff1a;
1&＃xff09;将根节点作为当前节点&＃xff0c;12大于10&＃xff0c;将10的右子节点&＃xff08;13节点&＃xff09;作为当前节点。
2&＃xff09;12与13比较&＃xff0c;将13的左子节点&＃xff08;12节点&＃xff09;作为当前节点。
3&＃xff09;12与12比较&＃xff0c;满足条件&＃xff0c;从当前节点去除data&＃xff0c;即id&＃61;12&＃xff0c;name&＃61;xm。
利用二叉查找树&＃xff0c;3次可找到匹配数据。如果在表中一条一条查找&＃xff0c;需要6次。

平衡二叉树&＃xff1a;
如果上面的二叉树这样构造&＃xff1a;

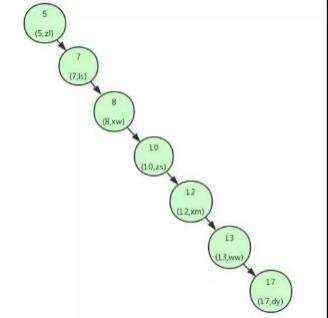
变成了一个链表&＃xff0c;查询id&＃61;17的用户信息&＃xff0c;需要查7次&＃xff0c;相当于全表扫描。导致这个现象是因为二叉查找树不平衡了。为了解决这个问题&＃xff0c;需要用平衡二叉树。
平衡二叉树又称 AVL 树&＃xff0c;在满足二叉查找树特性的基础上&＃xff0c;要求每个节点的左右子树的高度差不能超过 1。

B树&＃xff1a;
因为内存的易失性&＃xff0c;一般会将数据和索引存储到磁盘中。和内存比&＃xff0c;从磁盘读数据会慢很多&＃xff0c;所以应当减少读取次数。此外&＃xff0c;从磁盘读数据按照磁盘块来读取&＃xff0c;而非一条一条的读。
如果我们能把尽可能多的数据放进磁盘块中&＃xff0c;那一次磁盘读取操作就会读取更多数据&＃xff0c;那我们查找数据的时间也会大幅度降低。如果我们用树这种数据结构作为索引的数据结构&＃xff0c;那我们每查找一次数据就需要从磁盘中读取一个节点&＃xff0c;也就是我们说的一个磁盘块。我们都知道平衡二叉树可是每个节点只存储一个键值和数据的。那说明什么&＃xff1f;说明每个磁盘块仅仅存储一个键值和数据&＃xff01;那如果我们要存储海量的数据呢&＃xff1f;
可以想象到二叉树的节点将会非常多&＃xff0c;高度也会极其高&＃xff0c;我们查找数据时也会进行很多次磁盘 IO&＃xff0c;我们查找数据的效率将会极低&＃xff01;
为了解决平衡二叉树的这个弊端&＃xff0c;我们应该寻找一种单个节点可以存储多个键值和数据的平衡树。也就是我们接下来要说的 B 树。

图中的每个节点称为页&＃xff08;就是磁盘块&＃xff09;&＃xff0c;在MySQL中数据读取的基本单位都是页。每个节点存储了更多的键值和数据。子节点的个数一般称为阶&＃xff0c;上述图中B树为3阶B树。
查找id&＃61;28的用户信息&＃xff0c;流程如下&＃xff1a;
1&＃xff09;先找到根节点也就是页 1&＃xff0c;判断 28 在键值 17 和 35 之间&＃xff0c;那么我们根据页 1 中的指针 p2 找到页 3。
2&＃xff09;将 28 和页 3 中的键值相比较&＃xff0c;28 在 26 和 30 之间&＃xff0c;我们根据页 3 中的指针 p2 找到页 8。
3&＃xff09;将 28 和页 8 中的键值相比较&＃xff0c;发现有匹配的键值 28&＃xff0c;键值 28 对应的用户信息为&＃xff08;28&＃xff0c;bv&＃xff09;。

B&＃43;树&＃xff1a;

B&＃43;树是对B树的进化&＃xff0c;其不同&＃xff1a;
1&＃xff09;B&＃43;树非叶子节点不存储数据&＃xff0c;仅存储键值&＃xff0c;B树则存储键值和数据&＃xff08;为什么这么做&＃xff1f;数据库中页的大小是固定的&＃xff0c;InnoDB中默认是16KB&＃xff0c;如果不存数据&＃xff0c;就可以存更多的键值&＃xff0c;树的阶数会更大&＃xff0c;树就会更矮胖&＃xff0c;查找数据进行磁盘IO的次数就会减少&＃xff0c;查询效率快&＃xff09;。一般根节点是常驻内存的。
2&＃xff09;B&＃43;树索引的所有数据存储在叶子节点&＃xff0c;而且数据是按照顺序排列的&＃xff08;使得范围查找、排序查找、分组查找及去重查找很简单&＃xff0c;而B树因为数据分散在各个节点&＃xff0c;实现这一点很不容易&＃xff09;&＃xff0c;B&＃43;树的叶子节点中的数据通过单向链表连接&＃xff0c;各个页之间通过双向链表连接。
通过上图可以看到&＃xff0c;在 InnoDB 中&＃xff0c;我们通过数据页之间通过双向链表连接以及叶子节点中数据之间通过单向链表连接的方式可以找到表中所有的数据。
在 MySQL 中&＃xff0c;B&＃43; 树索引按照存储方式的不同分为聚集索引和非聚集索引。

利用聚集索引查找数据
现在假设我们要查找 id>&＃61;18 并且 id<40 的用户数据。对应的 sql 语句为&＃xff1a;

select * from user where id>&＃61;18 and id<40;

其中id为主键&＃xff0c;具体的查找过程如下&＃xff1a;
1&＃xff09;一般根节点常驻内存的&＃xff0c;页1已经在内存中了&＃xff0c;不用读磁盘&＃xff0c;直接内存读取。
在内存中页1查找id>&＃61;18 and id<40或者范围值&＃xff0c;先找到id&＃61;18的键值。从页1找到指针p2&＃xff0c;定位到页3。
2&＃xff09;从磁盘中读取页3&＃xff0c;然后将页3放入内存中&＃xff0c;然后进行查找&＃xff0c;可以找到键值18&＃xff0c;然后拿到页3中的指针p1&＃xff0c;定位到页8。
3&＃xff09;将页8读取到内存中&＃xff0c;根据二分查找法定位到键值18, 因为是范围查找&＃xff0c;而且此时所有的数据又都存在叶子节点&＃xff0c;并且是有序排列的&＃xff0c;那么我们就可以对页 8 中的键值依次进行遍历查找并匹配满足条件的数据。
我们可以一直找到键值为 22 的数据&＃xff0c;然后页 8 中就没有数据了&＃xff0c;此时我们需要拿着页 8 中的 p 指针去读取页 9 中的数据。
4&＃xff09;因为页 9 不在内存中&＃xff0c;就又会加载页 9 到内存中&＃xff0c;并通过和页 8 中一样的方式进行数据的查找&＃xff0c;直到将页 12 加载到内存中&＃xff0c;发现 41 大于 40&＃xff0c;此时不满足条件。那么查找到此终止。
具体流程图&＃xff1a;

利用非聚集索引查找数据
查找幸运数字为33的用户信息&＃xff0c;需要回表。