慢速特征分析简介

我最近在波鸿鲁尔大学开始了机器学习的博士学位研究。 我加入的小组的主要研究主题之一是慢特征分析&＃xff08;SFA&＃xff09;。 要学习一个新主题&＃xff0c;我喜欢看示例和直观的解释&＃xff0c;如果可能的话&＃xff0c;让自己沉浸在数学上的严谨中。 我为其他喜欢以类似方式接触学科的人写了这篇博客文章&＃xff0c;因为我认为SFA既强大又有趣。

在本文中&＃xff0c;我将以一个应用SFA的代码示例为指导&＃xff0c;以帮助激发该方法。 然后&＃xff0c;我将详细介绍该方法背后的数学原理&＃xff0c;最后提供指向该材料上其他良好资源的链接。

1.确定一个平滑的潜在变量

SFA是一种无监督的学习方法&＃xff0c;可以从时间序列中提取最平滑&＃xff08;最慢&＃xff09;的基础功能或特征 。 这可以用于降维&＃xff0c;回归和分类。 例如&＃xff0c;我们可以有一个高度不稳定的级数&＃xff0c;该级数由更好的行为潜变量确定。

让我们开始生成时间序列D和S&＃xff1a;

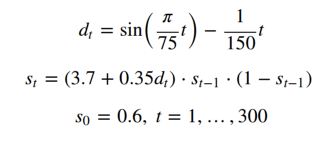
这称为后勤图。 通过绘制序列S &＃xff0c;我们可以检查其混沌性质。 驱动上面曲线的行为的基本时间序列D简单得多&＃xff1a;

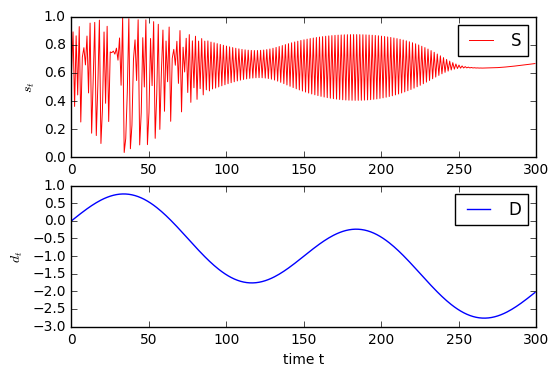
我们如何从不稳定的时间序列中确定简单的基础驱动力&＃xff1f;

我们可以使用SFA来确定功能最缓慢变化的功能。 在我们的情况下&＃xff0c;我们将以S之类的数据开始&＃xff0c;以D结束&＃xff0c;而不必事先知道S是如何生成的。

SFA的实现旨在寻找线性输入的特征。 但是从示例中我们可以看到&＃xff0c;驱动力D是高度非线性的&＃xff01; 这可以通过首先对时间序列S进行非线性扩展&＃xff0c;然后找到扩展数据的线性特征来解决。 通过这样做&＃xff0c;我们找到了原始数据的非线性特征。

让我们通过在上面堆叠S的延时副本来创建一个新的多元时间序列&＃xff1a;

接下来&＃xff0c;我们对数据进行三次扩展并提取SFA特征。 立方膨胀变成一个4维向量[A&＃xff0c;B&＃xff0c;C&＃xff0c;d]ᵀ与元件t³&＃xff0c;t²v&＃xff0c;电大&＃xff0c;吨 ²&＃xff0c;电视&＃xff0c;t代表不同T&＃xff0c;U&＃xff0c;V∈{A&＃xff0c;B的34元素矢量&＃xff0c;c&＃xff0c;d}。

请记住&＃xff0c;每个问题要添加的最佳时间延迟副本数各不相同。 或者&＃xff0c;如果原始数据的维数太高&＃xff0c;则需要进行降维&＃xff0c;例如使用主成分分析 。

因此&＃xff0c;将以下内容视为该方法的超参数&＃xff1a;维数展开&＃xff08;缩小&＃xff09;方法&＃xff0c;展开后的输出尺寸&＃xff08;缩小&＃xff09;和要找到的慢特征数量。

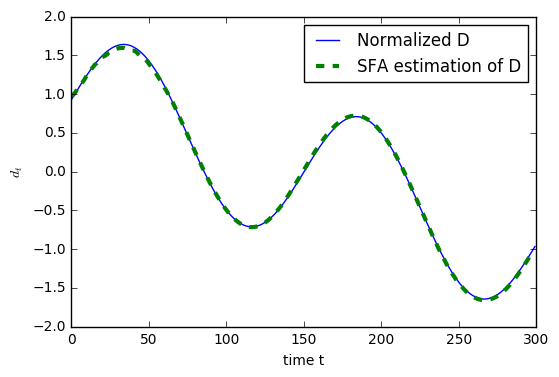
现在&＃xff0c;在添加延时复制后&＃xff0c;时间序列的长度从300更改为297。因此&＃xff0c;慢特征时间序列的相应长度也为297。 为了在此处更好地进行可视化&＃xff0c;我们通过在第一个值之前加上最后一个值两次来将其长度更改为300。 SFA发现的特征的均值和单位方差为零&＃xff0c;因此我们在可视化结果之前也将D归一化。

即使仅考虑300个数据点&＃xff0c;SFA功能也几乎可以完全恢复基础源-令人印象深刻&＃xff01;

2.那么到底发生了什么&＃xff1f;

从理论上讲&＃xff0c;SFA算法接受一个&＃xff08;多元&＃xff09;时间序列X和一个整数m来表示输入&＃xff0c;该整数m指示要从该序列中提取的特征数量&＃xff0c;其中m小于时间序列的维数。 该算法确定m个函数

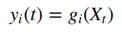
这样使得每个y 1的两个连续时间点的平方时间导数的平方最小。 直观地&＃xff0c;我们希望最大化功能的慢度&＃xff1a;

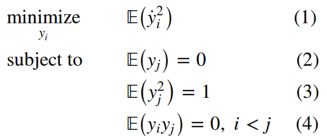
其中的点表示时间导数&＃xff0c;在离散情况下&＃xff1a;

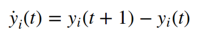
目标函数&＃xff08;1&＃xff09;测量特征的慢度。 零均值约束&＃xff08;2&＃xff09;使特征的第二矩和方差相等&＃xff0c;并简化了表示法。 单位方差约束&＃xff08;3&＃xff09;放弃常数解。

最终约束&＃xff08;4&＃xff09;对我们的特征进行解相关&＃xff0c;并导致其缓慢性排序。 这意味着我们首先找到最慢的特征&＃xff0c;然后找到与它之前的正交的下一个最慢的特征&＃xff0c;依此类推。 对功能进行解相关可确保我们捕获最多的信息。

在下文中&＃xff0c;我浏览了重要的细节并跳过了步骤&＃xff0c;但是为了完整起见&＃xff0c;我想将其包括在内。 我建议也查看下面的链接以获取更详尽的解释。

让我们只考虑线性特征&＃xff1a;

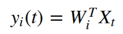
时间序列X可以是“原始数据”或它的非线性扩展&＃xff0c;请参见上面的示例。 请记住&＃xff0c;即使这些是扩展数据的线性特征&＃xff0c;它们仍然可以是原始数据的非线性特征。

假设均值X为零&＃xff0c;则通过求解广义特征值问题 AW &＃61; BWΛ找到线性特征。 我们确定米特征值-特征向量的元组&＃xff08;λᵢ&＃xff0c;Wᵢ&＃xff09;&＃xff0c;使得A &＃61;Wᵢλᵢ 乙 Wᵢ&＃xff0c;在那里我们有

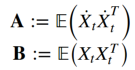
标量λᵢ表示特征的慢度&＃xff0c;即λᵢ越小 &＃xff0c;相应y varying的变化就越慢。 如果您熟悉广义特征值问题&＃xff0c;请注意此处的特征值在增加&＃xff0c;而不会减少。 最后&＃xff0c;特征向量Wᵢ是定义我们学习特征的变换向量。

3.进一步阅读

原始论文&＃xff1a; https : //www.ini.rub.de/PEOPLE/wiskott/Reprints/WiskottSejnowski-2002-NeurComp-LearningInvariances.pdf

SFA在分类中的应用&＃xff1a; http : //cogprints.org/4104/1/Berkes2005a-preprint.pdf

上面的示例改编自&＃xff1a; http : //mdp-toolkit.sourceforge.net/examples/logmap/logmap.html

From: https://hackernoon.com/a-brief-introduction-to-slow-feature-analysis-18c901bc2a58