零基础入门神经网络Matlab学习笔记

零基础快速入门Matlab神经网络,以通俗易懂的原理讲解并配套实战源码。包含RBF、BP、自组织竞争、SOM、Hopfield、SVM及粒子群（PSO）等神经网络的讲解。初学神经网络推荐。具体视频及源码、PPT已上传，下载请见：

https://download.csdn.net/download/qq_32809093/12008338

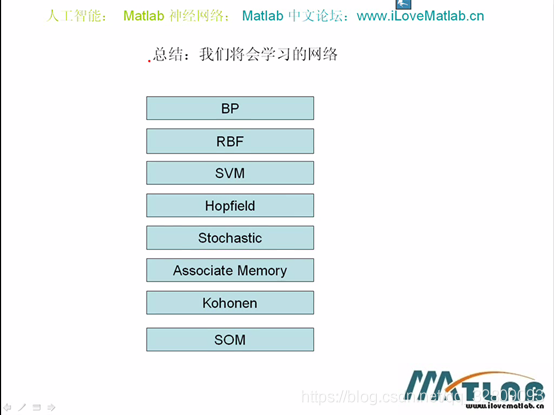
1 神经网络的6个基本问题

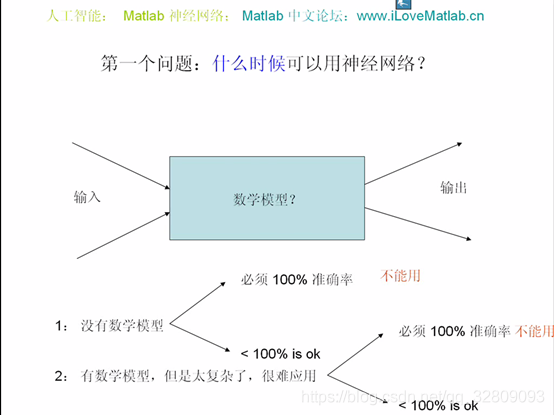
神经网络就是一个黑盒子，谁也不能保证其能百分百准确，所以如果系统要求百分百准确率，则不要使用神经网络进行控制

回归就是个预测

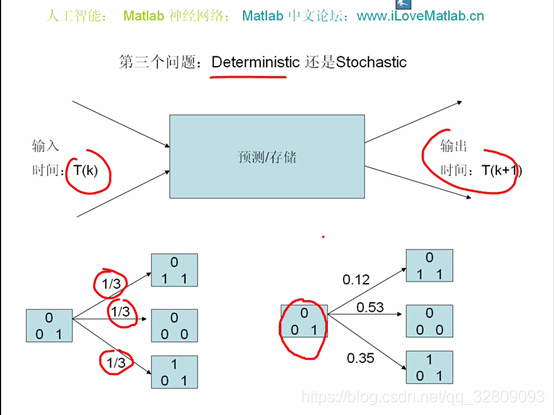
左边为预测，有三个数据表示其由三个组成部分组成，每次仅改变单个数据，每个组成部分比重相同（此都为1/3）

右边为存储，每次仅改变单个数据，每个组成部分比重不同

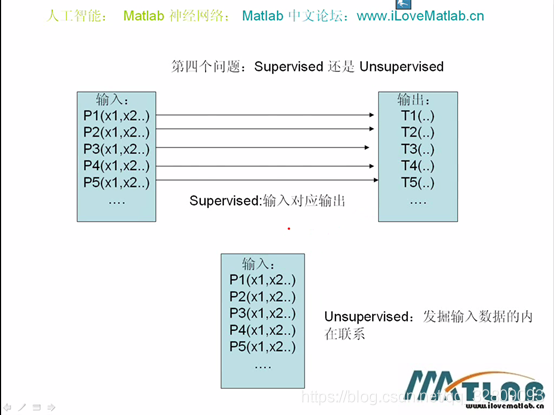
有监督（supervised）：输入输出一一对应。例如：BP网络（输入输出都有）

无监督（unsupervised）：只有输入，其目的为发掘输入数据的内在联系

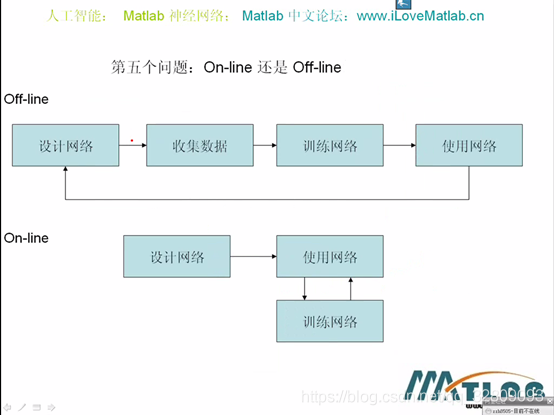
离线网络：需要先设计好网络，然后通过数据对网络进行训练后，再使用此网络

在线网络：可以边使用边训练网络（前期由于数据量少效果可能不是很好）

2 RBF神经网络

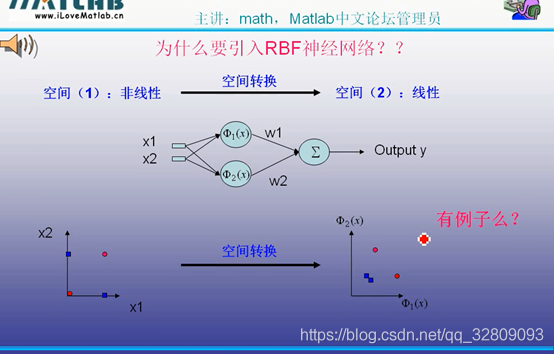
RBF网络本意：把输入的数据从一个空间转换到另外一个空间

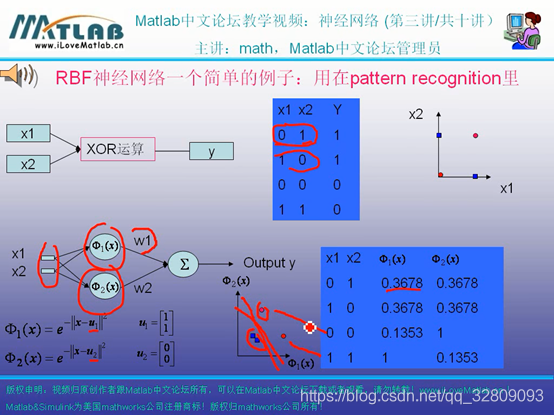
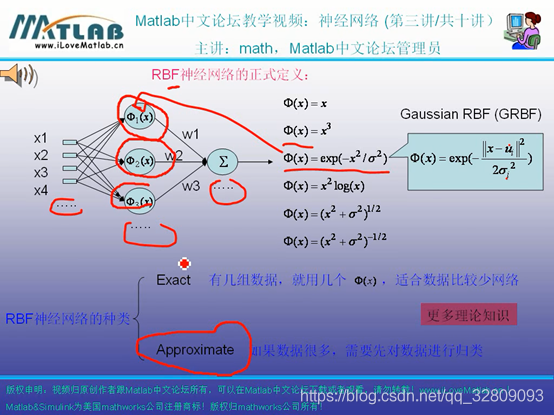
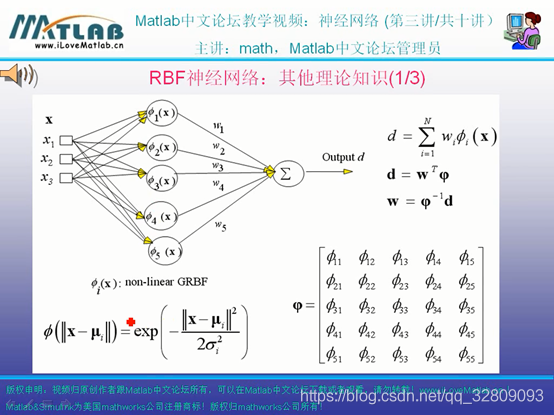
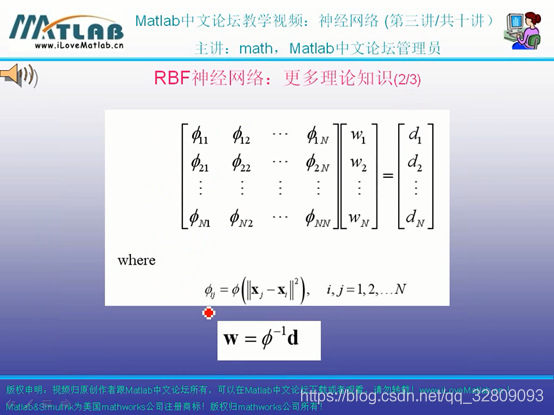
神经网络：只知道数据，不知道模型，要做一个网络，来模拟这个模型

数学回归：知道带参数的数学函数表达式，通过数据带入，可求出具体函数表达式

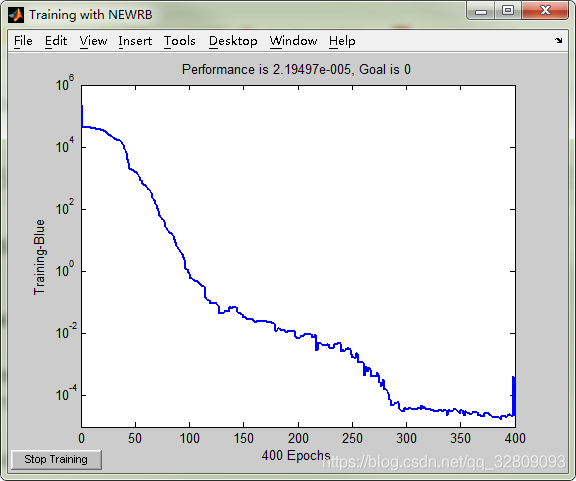
RBF网络程序1：使用随机生成数据，实现回归公式（使用newrb生成网络）

clc;
clear;
close all;

%产生输入，输出
ld=400; %学习数据的个数
%产生一个两维（对应x1、x2）的，共2*100个位于0-1之间的随机数据（或理解为100个二维数据）
x=rand(2,ld); % 0-1
x=(x-0.5)*1.5*2; % -1.5-1.5(改变x的取值范围，利于观察)
%提取产生的输入数据
x1=x(1, : );% x1为x的第一行
x2=x(2, : );% x2为x的第二行
F=20+x1.^2-10*cos(2*pi*x1)-10*cos(2*pi*x2);%产生输出数据

%创建并训练网络
net=newrb(x,F);%创建RBF网络，其自己会进行训练

%generate the testing data 产生模拟数据
interval=0.1; %间隔为0.1
[i, j]=meshgrid(-1.5:interval:1.5);%产生间隔为0.1，且位于-1.5-1.5之间的二维方框数据i和j,
row=size(i);
tx1=i(:);%将i转换成一维数据tx1
tx1=tx1&＃39;;
tx2=j(:);%将j转换成一维数据tx2
tx2=tx2&＃39;;
tx=[tx1;tx2];%将x1,x2合并转换为输入tx

%testing 画出模拟函数
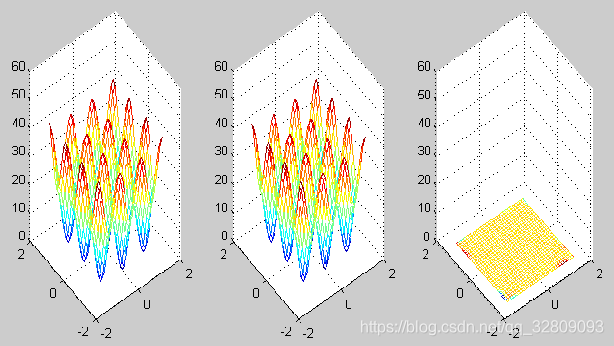
ty=sim(net,tx);%将tx带入网络进行模拟，输出为ty

v=reshape(ty,row);
figure
subplot(1,3,2)
mesh(i,j,v);%绘制i,j输入对应输出v曲线
zlim([0,60])

%plot the original function 画出原函数
interval=0.1;
[x1, x2]=meshgrid(-1.5:interval:1.5);
F = 20+x1.^2-10*cos(2*pi*x1)-10*cos(2*pi*x2);%F为理想输出
subplot(1,3,1)
mesh(x1,x2,F);%绘制x1,x2输入对应输出F曲线
zlim([0,60])

%plot the error 画出偏差
subplot(1,3,3)
mesh(x1,x2,F-v);%绘制x1,x2输入对应输出F-v曲线。F-v为理想输出与神经网络之间的误差
zlim([0,60])

RBF网络程序2：使用随机生成数据，实现回归公式（使用newrbe生成网络）

%Generate some training data
clc;
clear;
interval=0.01;
x1=-1.5:interval:1.5;
x2=-1.5:interval:1.5;
F = 20+x1.^2-10*cos(2*pi*x1)-10*cos(2*pi*x2);
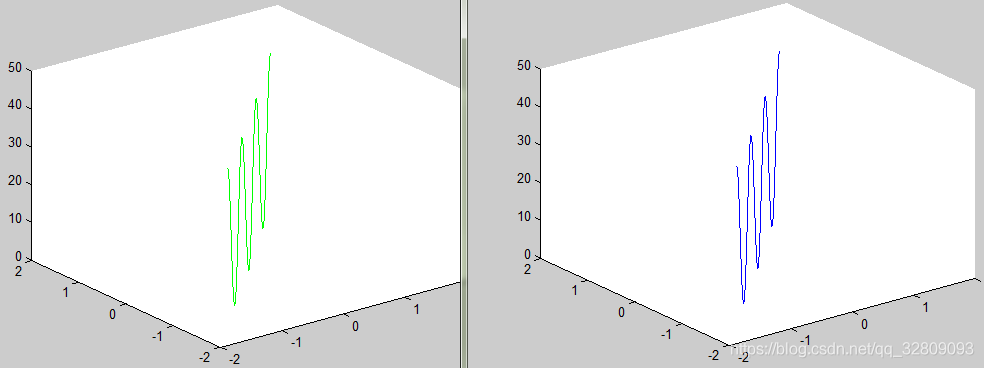
net=newrbe([x1;x2],F)%创建并训练网络

ty=sim(net,[x1;x2]);%将tx带入网络进行模拟，输出为ty
figure
plot3(x1,x2,F,&＃39;g&＃39;);%plot the original function 画出原函数
figure
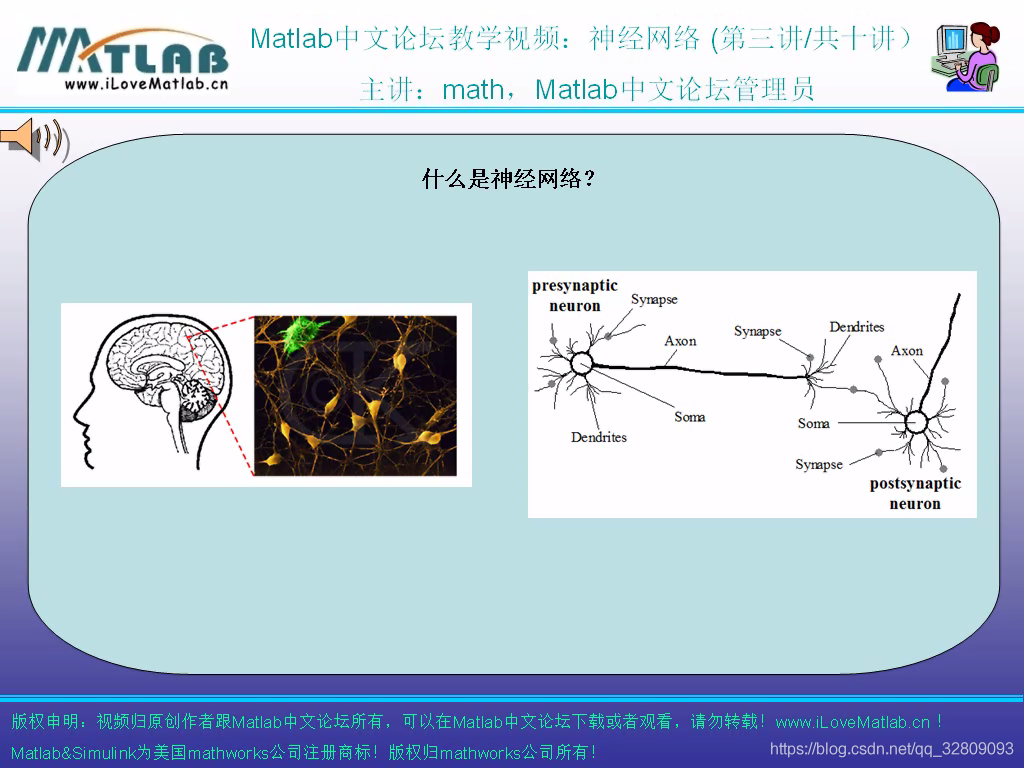
plot3(x1,x2,ty,&＃39;b&＃39;);%testing 画出模拟函数

3 BP神经网络

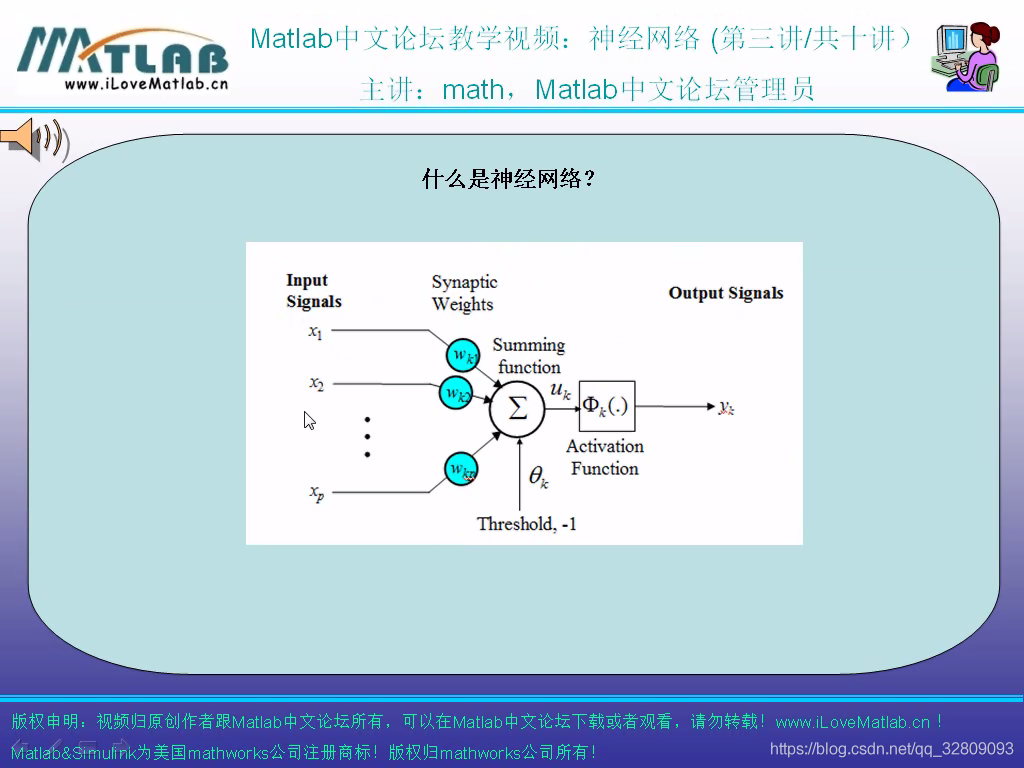
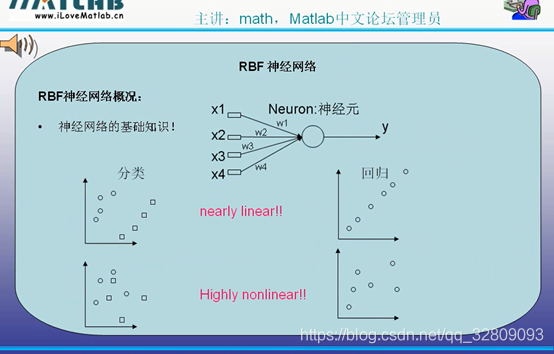
神经网络：怎么利用机器语言模仿人脑，来做决定的过程

理性世界：每一件事情的发生，都是由于其他事情造成的

所有控制、预测、统计都可以使用神经网络。

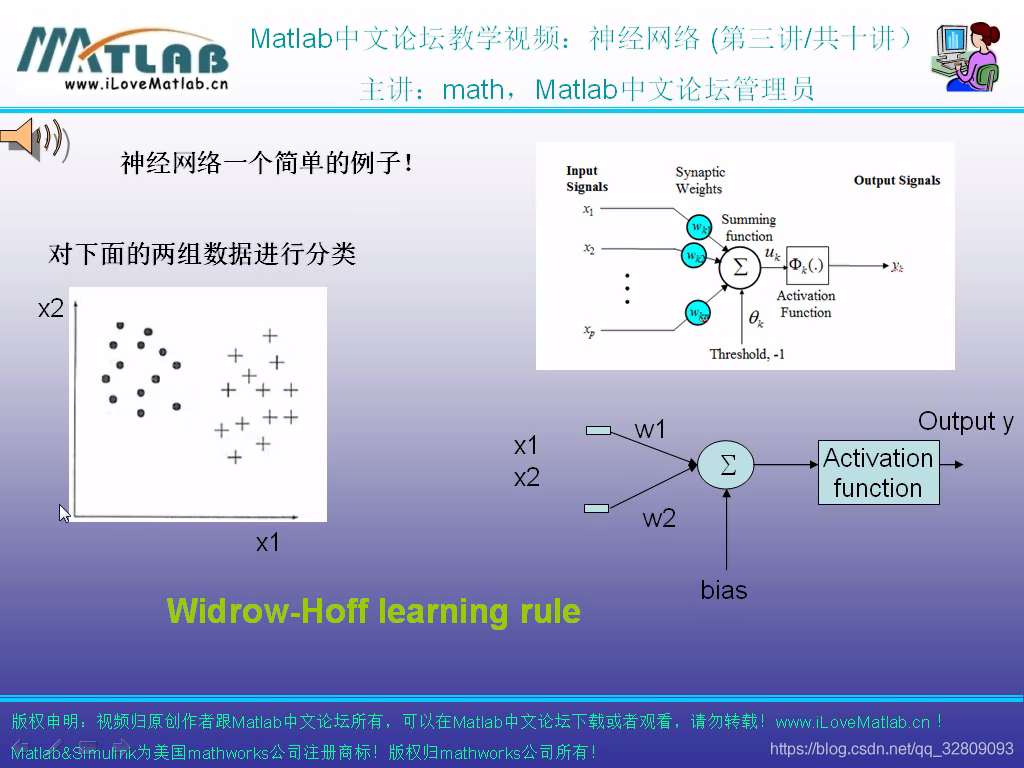
w1、w2权重的调整是减少误差的过程

一层网络可能不能进行非线性分类，所以引入多层神经网络

BP（Backpropagation）：从后往前来更新权重

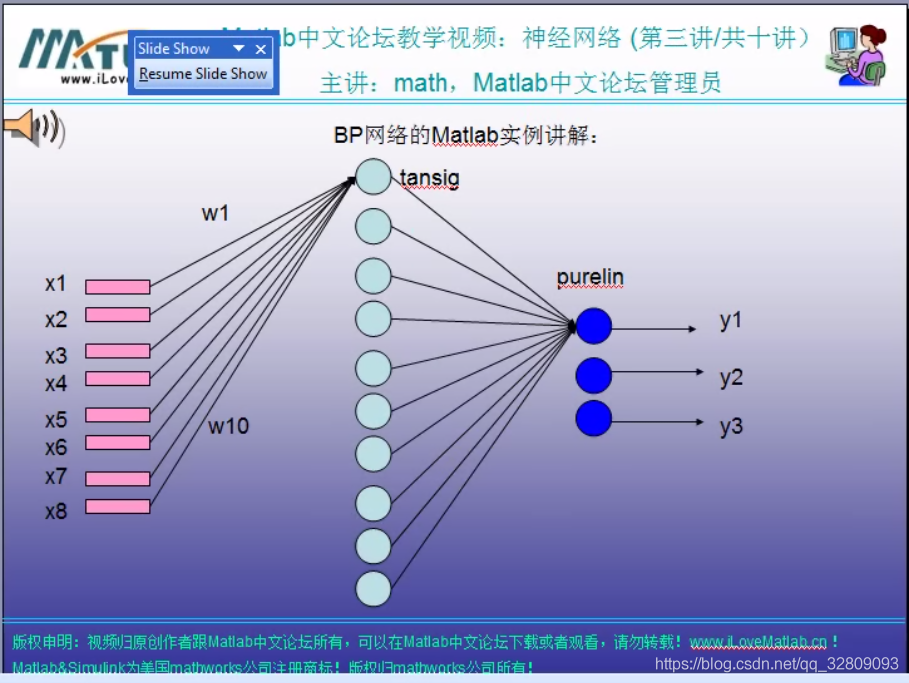
BP网络程序：对人脸角度进行预测

%function mytest()
%一共有15张人脸图片，每张图片提取八个数据，T为对应方向输出
clc;
images=[ ];  
M_train=3;%表示人脸
N_train=5;%表示方向   分别为（左110   左中101   中001    右中110   右101）
sample=[];  
pixel_value=[];
sample_number=0;

  for j=1:N_train
      for i=1:M_train
    str=strcat(&＃39;Images\&＃39;,num2str(i),&＃39;_&＃39;,num2str(j),&＃39;.bmp&＃39;); %读取图像，连接字符串形成图像的文件名。
    img= imread(str);  
    [rows cols]= size(img);%获得图像的行和列值。
     img_edge=edge(img,&＃39;Sobel&＃39;);

    
     %由于在分割图片中我们可以看到这个人脸的眼睛部分也就是位于分割后的第二行中，位置变化比较大，而且眼睛边缘检测效果很好
     
     sub_rows=floor(rows/6);%最接近的最小整数,分成6行
     sub_cols=floor(cols/8);%最接近的最小整数，分成8列
     sample_num=M_train*N_train;%前5个是第一幅人脸的5个角度
    
     sample_number=sample_number+1;
     for subblock_i=1:8 %因为这还在i，j的循环中，所以不可以用i 
           block_num=subblock_i;
           pixel_value(sample_number,block_num)=0;  
            for ii=sub_rows:(2*sub_rows)
             for jj=(subblock_i-1)*sub_cols+1:subblock_i*sub_cols
                 pixel_value(sample_number,block_num)=pixel_value(sample_number,block_num)+img_edge(ii,jj);          
             end
            end     
     end  
  end
  end
  %将特征值转换为小于1的值
 max_pixel_value=max(pixel_value);
  max_pixel_value_1=max(max_pixel_value); 
  for i=1:3
      mid_value=10^i;
      if(((max_pixel_value_1/mid_value)>1)&&((max_pixel_value_1/mid_value)<10))
         multiple_num=1/mid_value; 
         pixel_value=pixel_value*multiple_num; 
         break;
      end
  end     
  

% T 为目标矢量 
    t=zeros(3,sample_number);
    %因为有五类，所以至少用3个数表示，5介于2的2次方和2的3次方之间
    for i=1:sample_number
        % if((mod(i,5)==1)||(mod(i,5)==4)||(mod(i,5)==0))
        if(i<=3)||((i>9)&&(i<=12))||((i>12)&&(i<=15))
            t(1,i)=1;
        end    
        %if((mod(i,5)==2)||(mod(i,5)==4)) 
        if((i>3)&&(i<=6))||((i>9)&&(i<=12))
            t(2,i)=1;
        end        
        %if((mod(i,5)==3)||(mod(i,5)==0)) 
        if((i>6)&&(i<=9))||((i>12)&&(i<=15))
            t(3,i)=1;
        end           
    end  
    
    
   

% NEWFF——生成一个新的前向神经网络 
% TRAIN——对 BP 神经网络进行训练 
% SIM——对 BP 神经网络进行仿真 

%  定义训练样本 
% P 为输入矢量 
P=pixel_value&＃39;
% T 为目标矢量 
T=t
size(P)
size(T)
% size(P)
% size(T)

%  创建一个新的前向神经网络  
net_1=newff(minmax(P),[10,3],{&＃39;tansig&＃39;,&＃39;purelin&＃39;},&＃39;traingdm&＃39;)%P为输入矩阵，minmax(P)为找出P的最大值与最小值作为输入数据的范围
%输出层为3（输出层有三个神经元），有一个中间层（隐藏层），此隐藏层有10个神经元
%若为[10,10,3],则为两个中间层，且每层10个神经元
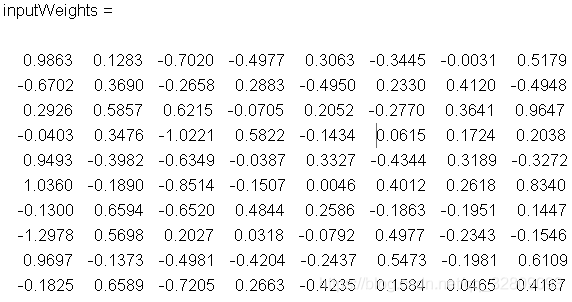
%  当前输入层权值和阈值 
inputWeights=net_1.IW{1,1} 
inputbias=net_1.b{1} 

                
%  当前网络层权值和阈值 
layerWeights=net_1.LW{2,1} 
layerbias=net_1.b{2} 

%  设置训练参数
net_1.trainParam.show = 50; 
net_1.trainParam.lr = 0.05; 
net_1.trainParam.mc = 0.9; 
net_1.trainParam.epochs = 10000; %每训练1000次显示一次结果
net_1.trainParam.goal = 1e-3; %训练误差要求0.001

%  调用 TRAINGDM 算法训练 BP 网络
[net_1,tr]=train(net_1,P,T); 

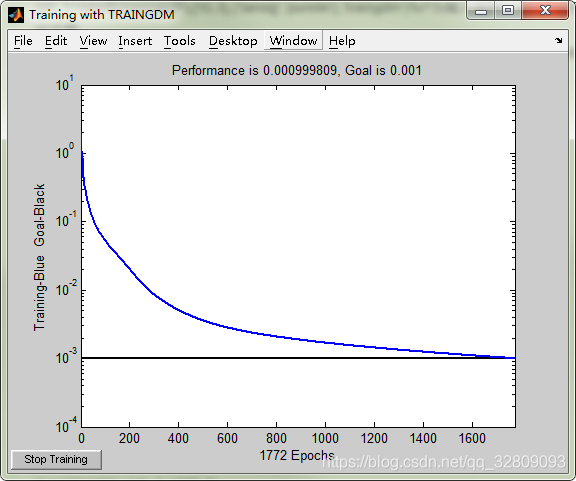
%  对 BP 网络进行仿真
A = sim(net_1,P); 
%  计算仿真误差  
E = T - A; 
MSE=mse(E) 

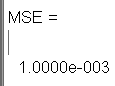
%随机举一个图片提取的8个数据代入网络判断（代入第一张图片数据）
x=[0.87 1.43 0.91 3.19 0.55 0 0.1 0]&＃39;;
sim(net_1,x)

可见其接近1 0 0 所以朝向为左。

4 自组织竞争网络及其matlab的实现

调整当前目录，导入基因数据txt文档

5 SOM神经网络理论及其Matlab实现

6 离散Hopfield神经网络(DHNN)及其MATLAB实现

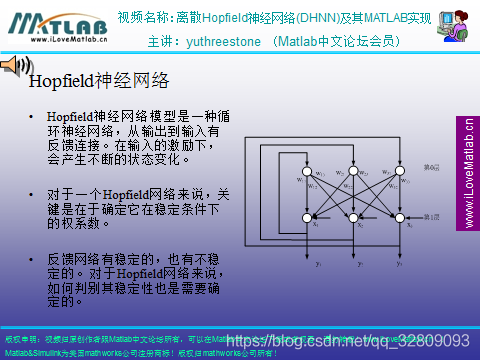
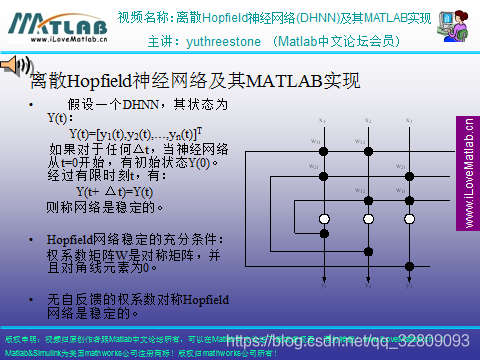
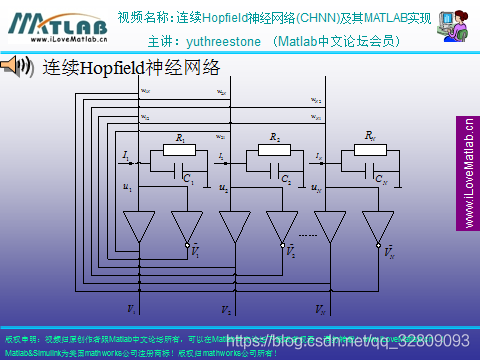
Hopfield是循环的，有反馈的闭环的网络

数字模型程序：

%0~9的数字模型
% 每个稳态由10*10的矩阵构成，该矩阵用于模拟阿拉伯数字点阵。
% 即将数字划分成10*10方阵，有数字的部分用1表示，空白处用-1表示
zero=[-1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
     -1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 -1 -1 -1 -1 1 1 -1;...
     -1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 -1 -1 -1 -1 1 1 -1;...
     -1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 -1 -1 -1 -1 1 1 -1;...
     -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1];
ZERO=imresize(zero,20);%对图像zero进行绘制并放大20倍
subplot(2,5,1)
imshow(ZERO)

One=[-1 -1 -1 -1 1 1 -1 -1 -1 -1;-1 -1 -1 -1 1 1 -1 -1 -1 -1;...
     -1 -1 -1 -1 1 1 -1 -1 -1 -1;-1 -1 -1 -1 1 1 -1 -1 -1 -1;...
     -1 -1 -1 -1 1 1 -1 -1 -1 -1;-1 -1 -1 -1 1 1 -1 -1 -1 -1;...
     -1 -1 -1 -1 1 1 -1 -1 -1 -1;-1 -1 -1 -1 1 1 -1 -1 -1 -1;...
     -1 -1 -1 -1 1 1 -1 -1 -1 -1;-1 -1 -1 -1 1 1 -1 -1 -1 -1];
 OnE=imresize(one,20);
 subplot(2,5,2)
 imshow(ONE)
 
 two=[-1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
       -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
        -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
       -1 1 1 -1 -1 -1 -1 -1 -1 -1;-1 1 1 -1 -1 -1 -1 -1 -1 -1;...
       -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1];
 TWO=imresize(two,20);
 subplot(2,5,3)
 imshow(TWO)
 
 three=[-1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
       -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
        -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
       -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
       -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1];
 THREE=imresize(three,20);
 subplot(2,5,4)
 imshow(THREE)
 
 four=[-1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 -1 -1 -1 -1 1 1 -1;...
      -1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 -1 -1 -1 -1 1 1 -1;...
      -1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
      -1 1 1 1 1 1 1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
      -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1];
 FOUR=imresize(four,20);
 subplot(2,5,5)
 imshow(FOUR)
 
 five=[-1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
       -1 1 1 -1 -1 -1 -1 -1 -1 -1;-1 1 1 -1 -1 -1 -1 -1 -1 -1;...
       -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
       -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
       -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1];
 FIVE=imresize(five,20);
 subplot(2,5,6)
 imshow(FIVE)
 
 six=[-1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
      -1 1 1 -1 -1 -1 -1 -1 -1 -1;-1 1 1 -1 -1 -1 -1 -1 -1 -1;...
      -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
      -1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 -1 -1 -1 -1 1 1 -1;...
      -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1];
 SIX=imresize(six,20);
 subplot(2,5,7)
 imshow(SIX)

 seven=[-1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
      -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
      -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
      -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
      -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1];
 SEVEN=imresize(seven,20);
 subplot(2,5,8)
 imshow(SEVEN)
 
 eight=[-1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
        -1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 -1 -1 -1 -1 1 1 -1;...
        -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
        -1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 -1 -1 -1 -1 1 1 -1;...
        -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1];
EIGHT=imresize(eight,20);
subplot(2,5,9)
imshow(EIGHT)

nine=[-1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
      -1 1 1 -1 -1 -1 -1 1 1 -1;-1 1 1 -1 -1 -1 -1 1 1 -1;...
      -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
      -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
      -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1];
 NINE=imresize(nine,20);
 subplot(2,5,10)
 imshow(NINE)

数字识别程序：

% ------------------------standard number array-----------------------
%标准数字数组
One=[-1 -1 -1 -1 1 1 -1 -1 -1 -1;-1 -1 -1 -1 1 1 -1 -1 -1 -1;...
     -1 -1 -1 -1 1 1 -1 -1 -1 -1; -1 -1 -1 -1 1 1 -1 -1 -1 -1;...
     -1 -1 -1 -1 1 1 -1 -1 -1 -1; -1 -1 -1 -1 1 1 -1 -1 -1 -1;...
     -1 -1 -1 -1 1 1 -1 -1 -1 -1; -1 -1 -1 -1 1 1 -1 -1 -1 -1;...
     -1 -1 -1 -1 1 1 -1 -1 -1 -1; -1 -1 -1 -1 1 1 -1 -1 -1 -1];
 
two=[-1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
     -1 -1 -1 -1 -1 -1 -1 1 1 -1;-1 -1 -1 -1 -1 -1 -1 1 1 -1;...
     -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1;...
     -1 1 1 -1 -1 -1 -1 -1 -1 -1;-1 1 1 -1 -1 -1 -1 -1 -1 -1;...
     -1 1 1 1 1 1 1 1 1 -1;-1 1 1 1 1 1 1 1 1 -1];

  
%   ----------------------plot standard number figure----------------- 
%绘制标准数字
 OnE=imresize(one,20);
 subplot(3,2,1)%subplot(m,n,p)在一个图像窗口切成m*n个小图像，其中此处显示第一个图像one(p从左到右从上到下增大)
 imshow(ONE)
 title(&＃39;stand number&＃39;)
 
 TWO=imresize(two,20);
 subplot(3,2,2)
 imshow(TWO)
 title(&＃39;stand number&＃39;)
 
%  ----------------------create hopfield net--------------------------
%生成hopfield网络
 T=[one;two]&＃39;;
 net=newhop(T);

 % -----------------------noise array(rand noise)-----------------
 %随机加入噪声
            rand(&＃39;state&＃39;,0);%初始化随机发生器
            for i=1:100
                a=rand;%产生0~1的随机数
                if a<0.1%加入10%的干扰，如果参数随机数小于0.1则标准数字取反
                   one(i)=-one(i);
                   two(i)=-two(i);
                end
            end
            no1=one;%噪声矩阵no1
            no2=two;
 
%  -------------------------plot noisy figure---------------
%绘制噪声数字
 subplot(3,2,3)
 NO1=imresize(no1,20);
 imshow(NO1)
 title(&＃39;noisy number&＃39;)

 subplot(3,2,4)
 NO2=imresize(no2,20);
 imshow(NO2)
 title(&＃39;noisy number&＃39;)

 
% --------------------------plot identify figure--------------
 
noise1={(no1)&＃39;};%将矩阵no1进行转置得到noise1
tu1=sim(net,{10,10},{},noise1);%将noise1通过神经网络仿真得到tu1
tu1{10}&＃39;
subplot(3,2,5)
imshow(imresize(tu1{10}&＃39;,20))%对图像tul取转置后进行绘制并放大20倍
title(&＃39;identify number&＃39;)

noise2={(no2)&＃39;};
tu2=sim(net,{10,10},{},noise2);
tu2{10}&＃39;
subplot(3,2,6)
imshow(imresize(tu2{10}&＃39;,20))
title(&＃39;identify number&＃39;)

tu1{10}&＃39;矩阵：

tu2{10}&＃39;矩阵：

当干扰为5%

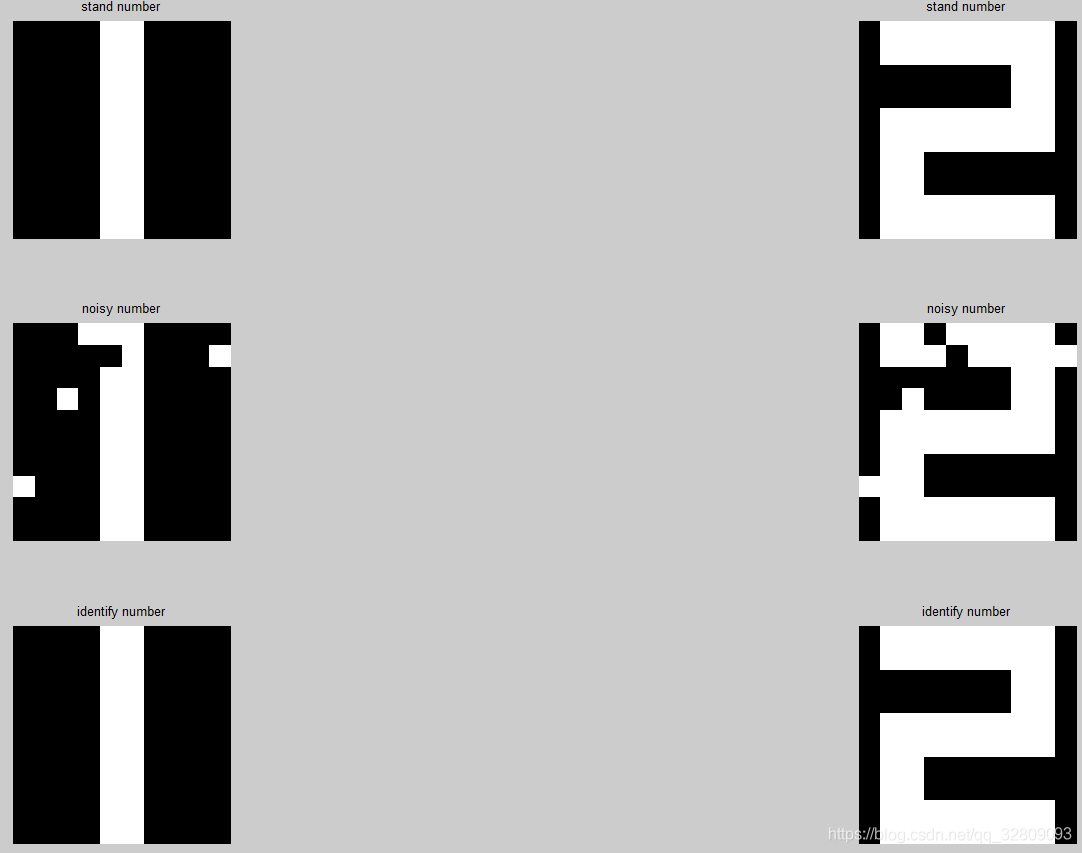
当干扰为10%

当干扰为20%

7 连续Hopfield神经网络(CHNN)及其MATLAB实现

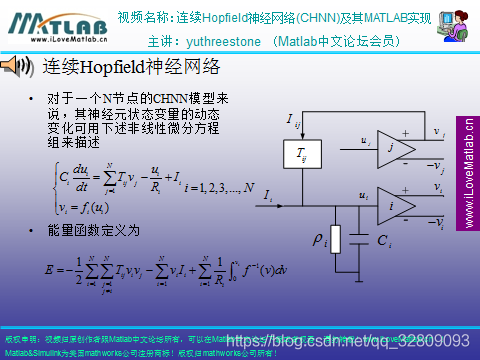
Hopfield网络求解TSP问题的仿真程序：chap8_5.m

% TSP Solving by Hopfield Neural Network

%function TSP_hopfield()
clear all;
close all;

% step 1 设置相关参数
A=1.5;
D=1;
u0=0.02;
step=0.01;

% step 2 读取8.txt中8个城市的坐标，计算各个城市之间的距离
N=8;
citys=load(&＃39;8.txt&＃39;);
Initial_Length=Initial_RouteLength(citys);        % 计算初始路径长度

DistanceCity=dist(citys,citys&＃39;);%每个城市与其它城市之间距离矩阵DistanceCity（1-1 1-2 ... 1-8）1-2指城市1与城市2之间的距离
%citys为8行*2列   citys&＃39;为2行*8列                                                                    % (2-1  2-2 ... 2-8)
% step 3 初始化神经元输入                                                                              % (8-1  8-2 ... 8-8)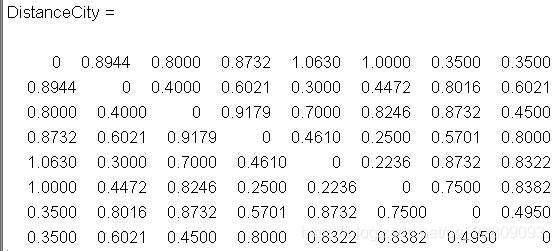                                                      
u=2*rand(N,N)-1;%产生随机数u范围为-1~1
U=0.5*u0*log(N-1)+u;%神经网络输入U
V=(1+tanh(U/u0))/2;%神经网络输出V

for k=1:1:2000%迭代次数2000步
    times(k)=k;
    
%     step 4 计算dU
    dU=DeltaU(V,DistanceCity,A,D);
    
%     step 5 及时更新U
    U=U+dU*step;
    
%     step 6 计算神经元输出V
    V=(1+tanh(U/u0))/2;
    
%     step 7 计算能量函数
    E=Energy(V,DistanceCity,A,D);
    Ep(k)=E;
    
%     step 8 检查路径合法性
    [V1,CheckR]=RouteCheck(V);
end

% step 9
if (CheckR==0)
    Final_E=Energy(V1,DistanceCity,A,D);   %最优能量
    Final_Length=Final_RouteLength(V1,citys);       % 计算最终路径长度
    disp(&＃39;迭代次数&＃39;);k

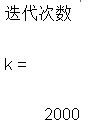
    disp(&＃39;寻优路径矩阵：&＃39;);V1

    disp(&＃39;最优能量函数：&＃39;);Final_E

    disp(&＃39;初始路程：&＃39;);Initial_Length

    disp(&＃39;最短路程：&＃39;);Final_Length

    PlotR(V1,citys);    % 寻优路径作图函数
else
    disp(&＃39;寻优路径无效&＃39;);
end

%绘制能量函数
figure(2);
plot(times,Ep,&＃39;r&＃39;);
title(&＃39;Energy Function Change&＃39;);
xlabel(&＃39;k&＃39;);
ylabel(&＃39;E&＃39;);

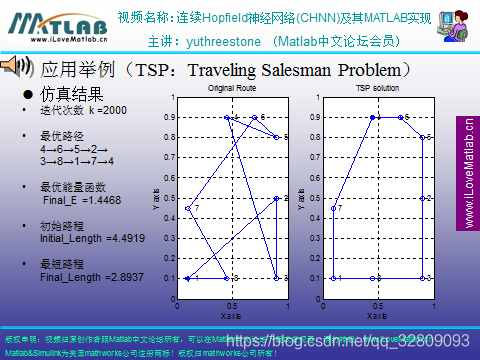
能量函数随迭代次数的变化：

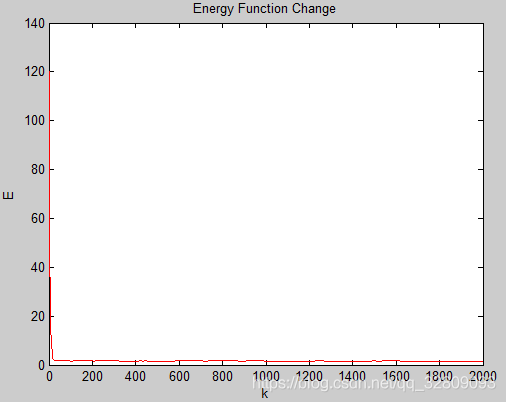
能量函数随时间单调下降，E的最小点对应问题的最优解

初始路径及优化后的路径：

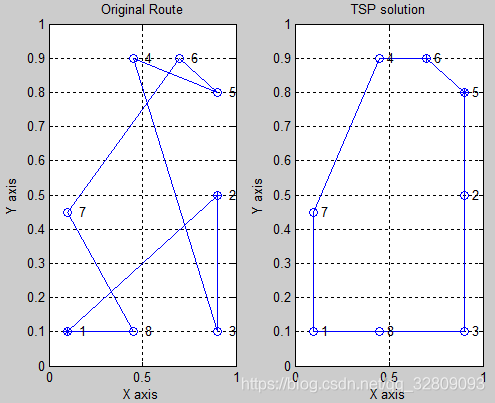
初始路径：1-2-3-4-5-6-7-8-1     优化路径：5-6-4-7-1-8-3-2-5

注：由于网络输入U初始选择的随机性，可能会导致初始化的寻优路径无效，当寻优失败时，需要重新运行优化程序。（90%以上可收敛得到最优解）

改变初试坐标：

8 SVM神经网络理论实际应用

9 粒子群算法（PSO）实现函数极值优化

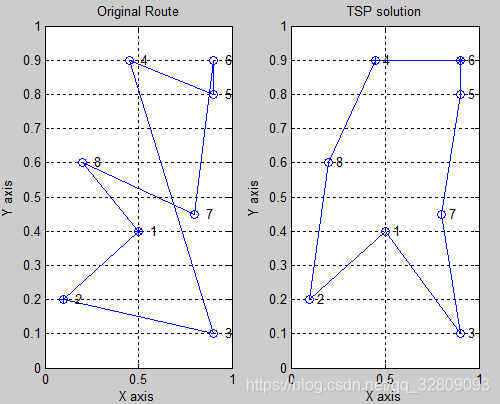
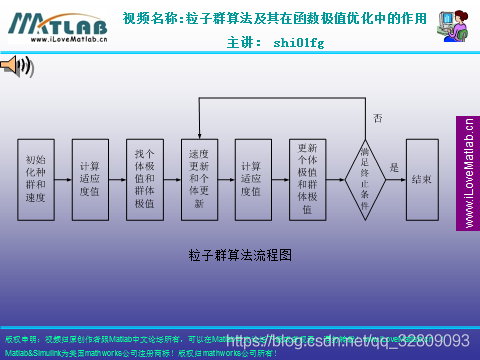
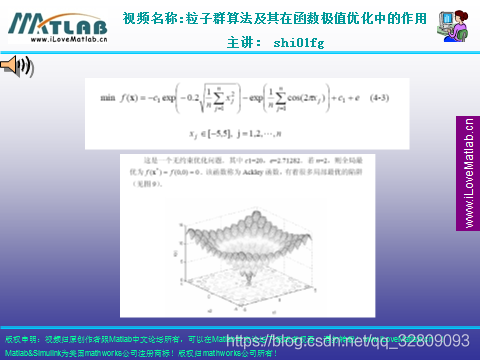
POS程序：

%% 清空环境
clc
clear

%% 参数初始化
%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;

maxgen=200;   % 进化次数  
sizepop=20;   %种群规模

Vmax=1;
Vmin=-1;
popmax=5;
popmin=-5;

%% 产生初始粒子和速度
for i=1:sizepop
    %随机产生一个种群
    pop(i,:)=5*rands(1,2);    %初始种群
    V(i,:)=rands(1,2);  %初始化速度
    %计算适应度
    fitness(i)=fun(pop(i,:));   %染色体的适应度
end

%找最好的染色体
[bestfitness bestindex]=min(fitness);
zbest=pop(bestindex,:);   %全局最佳
gbest=pop;    %个体最佳
fitnessgbest=fitness;   %个体最佳适应度值
fitnesszbest=bestfitness;   %全局最佳适应度值

%% 迭代寻优
for i=1:maxgen
    
    for j=1:sizepop
        
        %速度更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
        V(j,find(V(j,:)>Vmax))=Vmax;
        V(j,find(V(j,:)         
        %种群更新
        pop(j,:)=pop(j,:)+0.5*V(j,:);
        pop(j,find(pop(j,:)>popmax))=popmax;
        pop(j,find(pop(j,:)

        
        %自适应变异
        if rand>0.8
            k=ceil(2*rand);
            pop(j,k)=rand;
        end
      
        %适应度值
        fitness(j)=fun(pop(j,:));
        
        
        %个体最优更新
        if fitness(j)             gbest(j,:) = pop(j,:);
            fitnessgbest(j) = fitness(j);
        end
        
        %群体最优更新
        if fitness(j)             zbest = pop(j,:);
            fitnesszbest = fitness(j);
        end
        
    end
    yy(i)=fitnesszbest;    
        
end

%% 结果分析
plot(yy)
title([&＃39;适应度曲线  &＃39; &＃39;终止代数＝&＃39; num2str(maxgen)]);
xlabel(&＃39;进化代数&＃39;);ylabel(&＃39;适应度&＃39;);

zbest

10 LibSVM工具箱的下载、安装、使用教程