联邦学习:联邦场景下的时空数据挖掘

不论你望得多远，仍然有无限的空间在外边，不论你数多久，仍然有无限的时间数不清。——惠特曼《自己之歌》

1. 导引

时空数据挖掘做为智慧城市的重要组成部分，和我们的日常生活息息相关。如我们打开地图软件，会根据交通流量的预测为我们推荐路线；通过网约车软件下单，会为我们就近做订单匹配等等。

然而，时空数据挖掘在实际使用的过程中会面临一个难点，那就是跨平台协作。比如在疫情期间，我们需要对确诊病例的行程轨迹做追溯。而我们知道，一个人在行程中可能会使用多个软件，比如滴滴出行、共享单车乃至健身软件等。而如何让信息在不同平台间共享便成为难点。

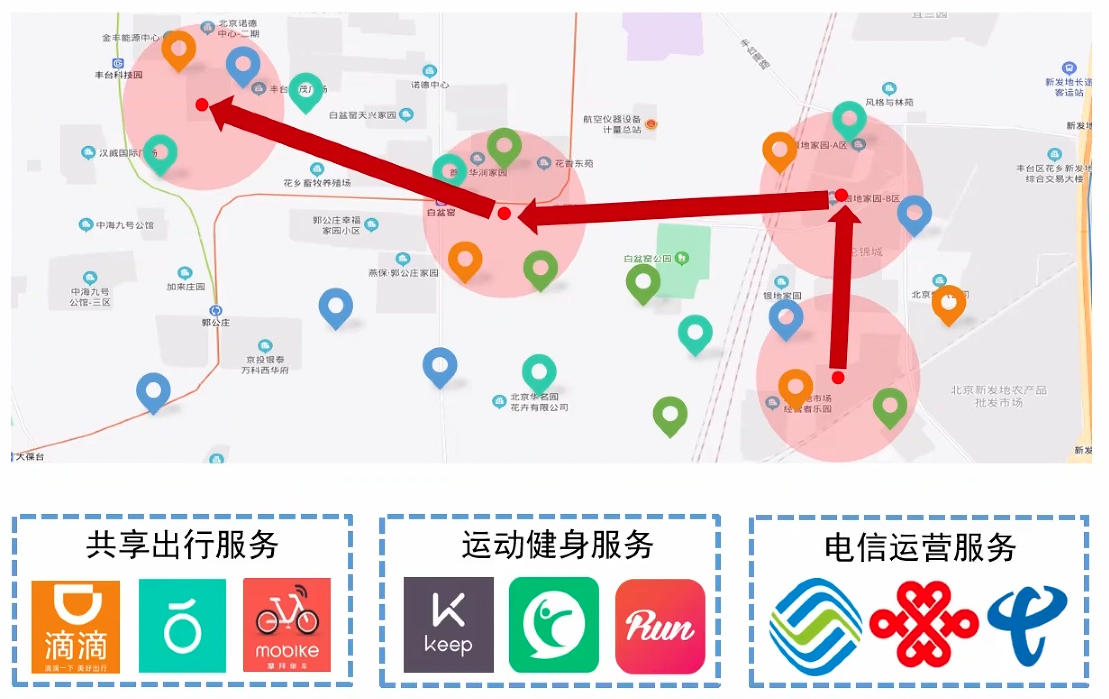
此外，在打车场景中也会面临此问题。一个用户在A于高峰期在平台A叫了一辆车，但是周围没有司机，订单因此取消了。然而，另一个平台B在周围有空闲的司机。而由于数据隔绝，该订单并不能够被B接收，这样就白白造成了资源的浪费，不仅降低了平台的收入也降低了用户的体验。

时空联邦计算是对该问题的一个有效解决方式。“数据不动计算动”的思想能够有效打破数据孤岛（data silo），实现跨平台的信息共享。

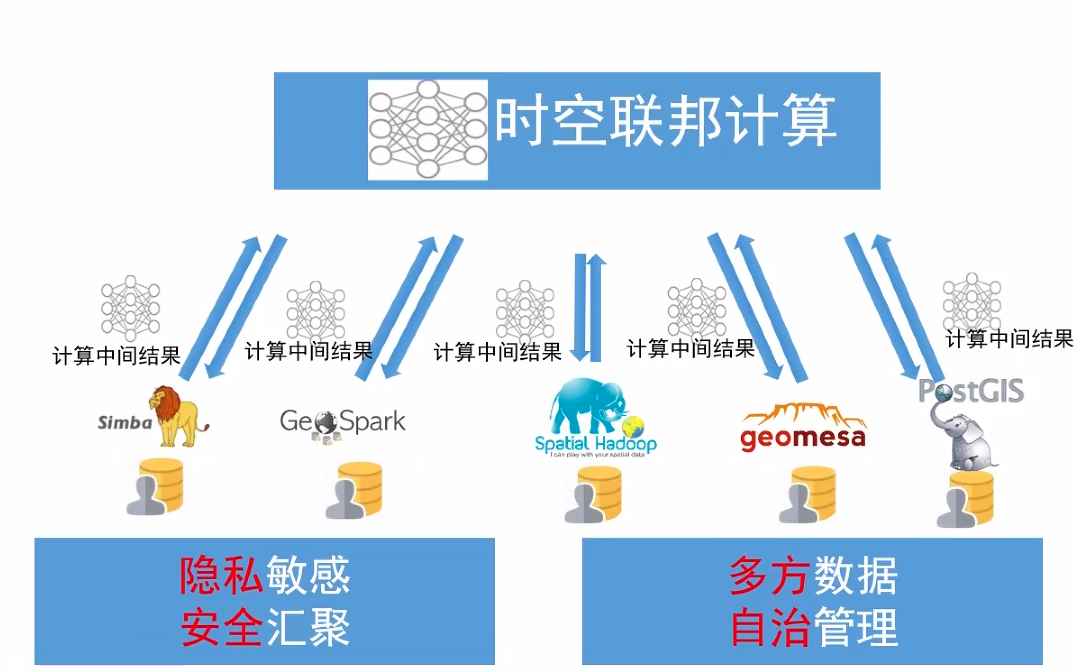
和传统联邦学习一样，时空联邦计算也可分为跨设备（cross-device）和跨筒仓（cross-silo）两种。跨设备类型中参与方为边缘设备，在我们此处的时空数据挖掘场景下常常是交通流量监测的传感器。而在跨筒仓的类型中参与方多为各企业或组织，在我们此处的场景下常常是各共享单车和网约车的服务商。在科研中，联邦时空数据挖掘会带来包括但不限于下列的几个议题：

• 对通信的效率要求更高，但是问题常常具有一定的容错性，这就允许我们采用随机算法进行加速。比如一个共享单车服务商可能会频繁处理“在地铁站方圆2km内有多少共享单车”，然而现实中有多个共享单车服务商，为了不逐一查询，我们可以用随机采样进行查询的方法来近似查询结果。

  
  



• 特别地，对于跨设备类型而言，可能还需要考虑各节点之间的空间关系，此时往往将各个节点及其之间的空间关系建模为图数据结构。

  
  



• 问题类型多样，可能还会牵涉到组合优化、强化学习等，导致每轮迭代的聚合内容不同于普通的联邦优化算法，

  
  

这里特别提一下北京航空航天大学的童咏昕组Big Data Analysis Group，近年来他们组在联邦学习和时空数据挖掘方面做了不少工作，大家可以特别关注下。

2. 联邦时空数据挖掘经典论文阅读

2.1 SIGKDD 2021:《Cross-Node Federated Graph Neural Network for Spatio-Temporal Data Modeling》

本篇文章的靓点在于用GRU网络学习各节点的时序数据的同时，用GNN去学习节点之间的拓扑关系信息。虽然用GNN学习网络拓扑信息也不是这篇论文首创了，早在2019年就有人这么做过^[2]，但将时间和空间一起考虑据我所知确实是首次。

论文将所有节点和其网络连接视为图\(G=(V, E)\)，节点\(i\in V\)的嵌入向量为\(v_i\)，边\(k\in E\)的嵌入向量为\(e_k\)，图的全局嵌入向量为\(u\)。图\(G\)的邻接矩阵\(W\)由带阈值的高斯核函数构造，满足\(W_{i,j}=d_{i,j} \text{ if } d_{i,j} \geqslant \kappa \text{ else } 0\)，这里\(d_{i,j} = \exp(-\frac{\text{dist}(i, j)^2}{\sigma^2})\)，\(\text{dist}(i, j)\)表示传感器\(i\)和\(j\)之间的公路网络距离，\(\sigma\)是所有距离的标准差。

每个节点\(i\)用编码器-解码器结构（其中编码器和解码器都为GRU）得到节点时序数据的预测信息：

\[ \begin{aligned}

&h_i = \text{Encoder}_i(x_i; \theta_{[i, 1]})\\

&\hat{y}_i = \text{Decoder}_i(x_i, [h_i; v_i]; \theta_{[i, 2]})

\end{aligned}

\]

然后计算损失函数

\[\mathcal{l}_i=\mathcal{l}(\hat{y}_i, y),

\]

这里\(x_i\)是节点\(i\)的输入时序数据，\(h_i\)是编码器GRU的最后一个状态, \(\hat{y}_i\)是预测标签，\(\theta_{[i, 1]}\)和\(\theta_{[i, 2]}\)分别是编码器和解码器对应的参数。

sever将所有节点的隐藏层向量集合\(\{h_i\}_{i\in V}\)做为图网络GN的输入，从而得到所有节点的嵌入向量集合\(\{v_i\}_{i\in V}\)。图网络的每一层都分为以下三步（论文共设置了两层并采用残差连接）：

① 计算更新后的边\(k\)的嵌入向量：

\[e_{k}^{\prime}=\text{MLP}_e \left(e_{k}, v_{r_{k}}, v_{s_{k}}, u\right)

\]

② 计算更新后的点\(i\)的嵌入向量(需要先聚合其邻边集合的信息)：

\[ v_{i}^{\prime} = \text{MLP}_v \left(\text{Aggregate}_{e\rightarrow v} \left(\{e_k^{\prime} | r_k = i\}\right), v_i, u \right)

\]

③ 计算更新后的全局嵌入向量(需要先聚合所有点和所有边的嵌入信息)：

\[ u^{\prime} = \text{MLP}_u\left(\text{Aggregate}_{e\rightarrow u}(\{e^{\prime}_k \}_{k\in E}), \text{Aggregate}_{v\rightarrow u}({\{v_i\}}_{i\in V}), u \right)

\]

对于图网络的第一层，论文设置\(v_i=h_i\)，\(e_k=W_{r_k, s_k}\)(\(W\)为邻接矩阵，\(r_k\)、\(s_k\)为边\(k\)对应的两个节点)，\(u\)为\(0\)向量。这里将图网络的参数记作\(\theta_{GN}\)。

综上，该论文的算法每轮迭代的流程可描述如下：

(1) server执行：

• 等待每个节点运行\(\text{ClientUpdate}\)，得到更新后的编码器-解码器参数\(\theta_i\)。


• 对所有节点更新后的编码器-解码器参数集合\(\{\theta_i\}_{i\in V}\)进行聚合：
  

  \[\overline{\theta} = \sum_{i\in V} \frac{N_i}{N}\theta_i
  
  \]

  
  


• 等待每个节点运行\(\text{ClientEncode}\)得到隐藏层向量\(h_i\)。


• 进行多轮迭代以更新图网络参数\(\theta_{GN}\)，在每轮迭代中依次进行以下操作：
  
  
  
  • 计算所有节点的点嵌入向量：
  
  

  \[ \{v_i\}_{i\in V} = \text{GN}\left(\{h_i\}_{i\in V}; \theta_{GN} \right)
  
  \]

  
  
  
  
  • 将\(\{v_i\}_{i\in V}\)发往各节点。
  
  
  • 等待每个节点运行\(\text{ClientBackward}\)得到\(\nabla_{v_i} \mathcal{l}_i\)并将其发往server。
  
  
  • 收集\(\{\nabla_{v_i} \mathcal{l}_i\}_{i\in V}\)，并从\(\{v_i\}_{i\in V}\)开始继续进行反向传播得到\(\{\nabla_{\theta_{GN}}\mathcal{l}_i\}_{i\in V}\)。
  
  
  • 更新图网络参数\(\theta_{GN}\)：
    

    \[\theta_{GN} = \theta_{GN} - \eta \sum_{i\in V}\nabla_{\theta_{GN}}\mathcal{l}_i
    
    \]

    
    
  
  
  
  


• 更新节点嵌入向量
  

  \[ \{v_i\}_{i\in V} = \text{GN}\left(\{h_i\}_{i\in V}; \theta_{GN} \right)
  
  \]

  
  


• 将\(\{v_i\}_{i\in V}\)发往client。

(2) 第\(i\)个client所执行操作的具体定义如下：

\(\text{ClientUpdate}\)

• 进行多轮的局部迭代以更新参数\(\theta_i\):
  

  \[\theta_i = \theta_i - \eta \nabla_{\theta_i} \mathcal{l}_i
  
  \]

  
  


• 将\(\theta_i\)发往server。

\(\text{ClientEncode}\)

• 计算\(h_i=\text{Encoder}_i(x_i; \theta_{[i, 1]})\)并发往server。

\(\text{ClientBackward}\)

• 计算\(\nabla_{v_i} \mathcal{l}_i\)并发往server。

2.2 TKDE 2021:《Efficient Approximate Range Aggregation over Large-scale Spatial Data Federation》^[2]

本文讨论了在联邦场景下的空间数据聚合查询，比如共享单车服务商就经常会处理“在地铁站方圆2公里内有多少量共享单车”这类查询。该算法在公共卫生响应、城市环境监测等领域都有广泛的应用。

设空间对象为\(\langle l_o, a_o\rangle\)，其中\(l_o\)是空间对象的位置，\(a_0\)是相应的测量属性，如\(l_0\)可以为出租车的GPS位置，\(a_0\)为其速度。

假定有\(K\)个client(数据筒仓)。\(O_{k}=\{o_1,o_2,\cdots,o_{n_{k}}\}\)为在第\(k\)个client中的空间对象集合，\(O\)为所有空间数据对象集合。因为论文采用横向联邦学习（数据划分），满足所有空间对象集合\(O=\bigcup_{k=1}^{K}\left\{O_{k}\right\}\)。

给定拥有空间数据对象集合\(O\)的联邦\(S\)，一个查询范围\(R\)与一个聚合函数\(F\)，则我们定义一个联邦范围聚合(Federated Range Aggregation， FRA)查询为：

\[Q(R, F)=F\left(\left\{a_{o} \mid o \in O, o \text { is within } R\right\}\right)

\]

而对于在联邦场景下的第\(k\)个client，则只能回答查询\(Q\left(R, F\right)_k=F\left(\left\{a_{0} \mid o \in O_{k}, o \text { is within } R\right\}\right)\)。注意\(R\)可以是圆型或矩形的。论文的算法就是要去获得查询结果的\(Q(R,F)\)近似值（出于效率考虑不要求遍历每个client以获得精确值）。

若假定有两个数据筒仓，筒仓1有10个空间数据对象，筒仓2有8个空间数据对象。则下图展示了对坐标(4,6)方圆3个坐标单位内的对象属性和进行查询（筒仓1对象标注为蓝色，筒仓2对象标注为红色）:

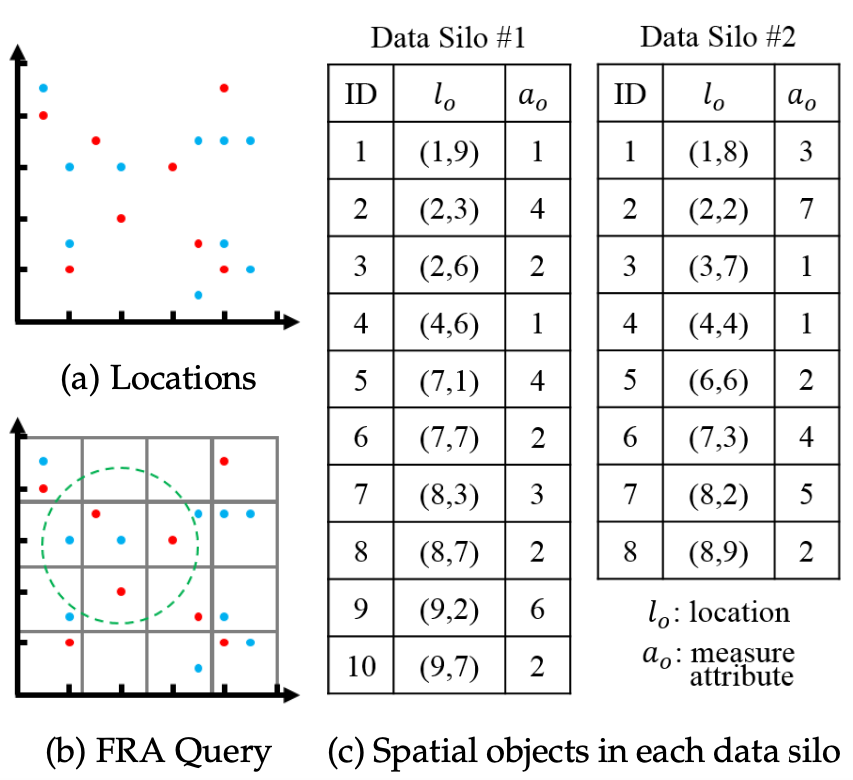
在运行联邦查询算法之前，第\(k\)个client需要先构建其中数据的网格索引集合\(g_k\)，然后将其发送到server。server将其聚合得到\(g=\{g_1, \cdots, g_K\}\)。

然后，给定查询范围\(R\)，聚合函数\(F\)，则回答查询\(Q(R, F)\)的流程可描述如下（若假定空间数据对象在不同节点间呈现IID分布）：

• 随机选取一个节点\(k\)

  
  



• 将\((R, F)\)发送到节点\(k\)。

  
  



• 从节点\(k\)接收查询结果\(res_k\)。

  
  



• 令\(sum = 0, sum_k = 0\)（前者为所有节点中对象的属性之和，后者为第\(k\)个节点中对象的属性之和）。

  
  



• 对网格索引集合\(g\)中的每一个与查询范围\(R\)有交集的网格\(i\)，执行：

  
  

  \[\begin{aligned}
  
  & sum = sum + F(\{a_o \mid o在网格i中 \})\\
  
  & sum_k = sum_k + F(\{a_o \mid o在网格i中且 i\in g_k \})
  
  \end{aligned}
  
  \]

  
  



• 计算\(ans = res_k \times( sum /sum_k)\)

  
  



• 返回\(ans\)

  
  

回到上面图中的例子，假定随机采中的节点为\(silo \#2\)。算法依次遍历左上角的\(3\times 3\)网格，计算出所有节点中空间对象的属性之和\(sum=4+0+0(\text{first row})+2+2+4(\text{second row})+4+1+4(\text{third row})=21\)，节点2中空间对象的属性之和\(sum_2 = 3+0+0+0+1+2+0+1+4=11\)，而节点2中在\(R\)范围内的空间对象属性之和\(res_2=1+2+1=4\)，则可得到范围\(R\)所有对象属性和的近似计算结果\(4 \times (21/11)=7.6\)。

其中，论文在节点\(k\)的本地查询过程中提出一种特殊的称为LSR-Forest的索引技术，为每个数据筒仓加速了本地的范围聚合查询。

整体算法流程描述如下：

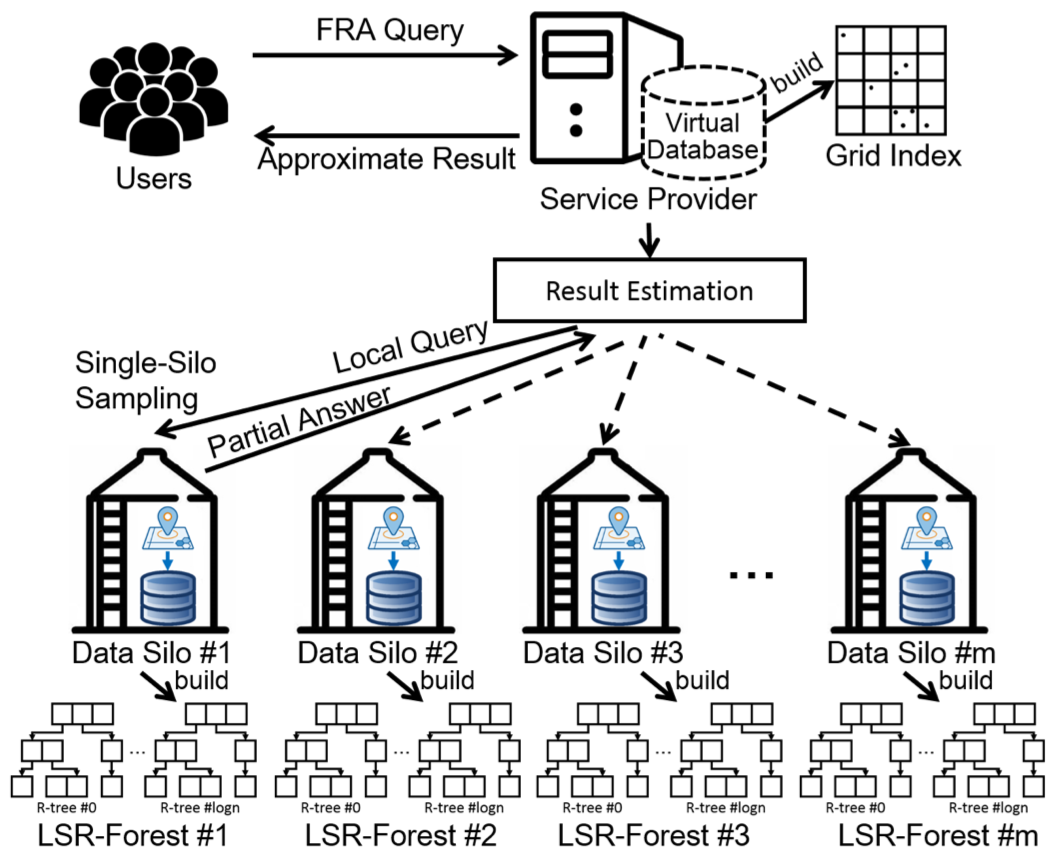
不过上述算法假定空间数据对象在不同节点间呈现IID分布，这样才能直接从来自某个随机节点的查询结果\(res_k\)（论文中称为partial answer，可视为一种有偏估计）推出所有节点的查询结果。 而对于Non-IID的情况，则需要将算法修改为：

• 随机选取一个节点\(k\)

  
  



• 将查询\((R, F)\)发送到节点\(k\)。

  
  



• 从节点\(k\)接收查询结果\(res_k^1,\cdots, res_k^{|g_k|}\)（其中\(res_k^i\)表示\(k\)节点内\(i\)网格中的对象属性和）。

  
  



• 令\(ans^{\prime} = 0\)。

  
  



• 对网格索引集合\(g\)中的每一个与查询范围\(R\)有交集的网格\(i\)，执行：

  
  

  \[\begin{aligned}
  
  & est^i = res_k^i\times \frac{F(\{a_o | o在网格i中 \})}{F(\{a_o | o在网格i中且 i\in g_k \})} \\
  
  & ans^{\prime} = ans^{\prime} + est^i
  
  \end{aligned}
  
  \]

  
  



• 返回\(ans^{\prime}\)

  
  

2.3 KDD 2022:《Fed-LTD: Towards Cross-Platform Ride Hailing via Federated Learning to Dispatch》^[3]

本篇论文旨在解决跨平台叫车问题，即多平台在不共享数据的情况下协同进行订单分配。本文的靓点在于将原本用于求解多时间步二分图最大匹配问题的强化学习算法扩展到联邦场景下，同时结合MD5+局部敏感性哈希保证了数据的隐私性。

设\(U\)为司机集合，\(u\in U\)表示一个司机，\(u.loc\)为该司机的位置（用网格坐标表示）; \(V\)为订单集合，\(v\in V\)表示一个订单，\(v.origin\)和\(v.destination\)分别为乘客目前位置和目的地位置，\(v.reward\)为订单的收入。司机和用户集合能够形成一个二分图\(G=(U\cup V, E)\)，这里每条边\(e=(u, v)\in E\)都有对应权重\(w(u, v)=v.reward\)。当\(u.loc\)和\(v.origin\)之间的距离超过阈值\(R\)时边会被截断。

定义\(\mathcal{M}\)是一个在二分图\(G\)上的匹配结果，该匹配结果为司机-订单对的集合，其中每个元素\((u, v)\)满足\(u\in U, v \in V\)且\(u\)和\(v\)只在\(\mathcal{M}\)中出现一次。我们定义以下功效函数做为\(\mathcal{M}\)中的边权和：

\[\text{SUM}(\mathcal{M}(G))=\sum_{(u, v) \in \mathcal{M}} w(u, v)

\]

给定二分图\(G\)，找到能够最大化\(\text{SUM}(\mathcal{M}(G))\)的匹配结果\(\mathcal{M}\)是经典的二分图最大匹配问题，可以用匈牙利算法在多项式时间内求解。不过在实际的订单分配场景下，订单和司机都是以在线（online）的形式到达的，基于批处理的模型在这种场景下被广泛应用。若给定批量序列\(\langle 1,2, \cdots, T\rangle\)，在\(t\)时刻待匹配的司机和订单形成二分图\(G^t\)， 此时订单分配问题可以定义如下：

\[\max \sum_{t=1}^{T} \text{SUM} \left(\mathcal{M}^{t}\left(G^{t}\right)\right)

\]

最朴素的方法是为每个批量分别进行二分图最大匹配。不过，在大规模历史数据的帮助下，基于强化学习的方法能够取得更好的效果。

我们将司机视为智能体，他们的地理位置视为状态，选定接下某个订单或保持空闲为动作，价值函数为在特定状态的期望累积奖励：

\[\mathcal{V}(s^t) = \mathbb{E}[\sum_{t} r^t |s^t]

\]

这里\(s^t\)是状态向量，\(r^t\)是第\(t\)个批量的奖励和。价值函数按照Bellman方程来更新：

\[\mathcal{V}\left(s^{t}\right) \leftarrow \mathcal{V}\left(s^{t}\right)+\alpha \cdot \sum_{u}\left(r_{u}^{t}+\gamma \mathcal{V}\left(s_{v}^{t+1}\right)-\mathcal{V}\left(s_{u}^{t}\right)\right)

\]

这里\(u\)和\(v\)分别是司机和订单，\(\alpha\)是学习率，\(\gamma\)是折扣因子。然后，分配决策可以由各个参与方基于学得的价值来决定。

\[w(u, v)=v.reward+\gamma \mathcal{V}\left(s_{e}^{t+1}\right)-\mathcal{V} \left(s_{u}^{t}\right)

\]

在对二分图的边权进行更新后，就能够使用匈牙利算法来求解本地分配决策问题了。

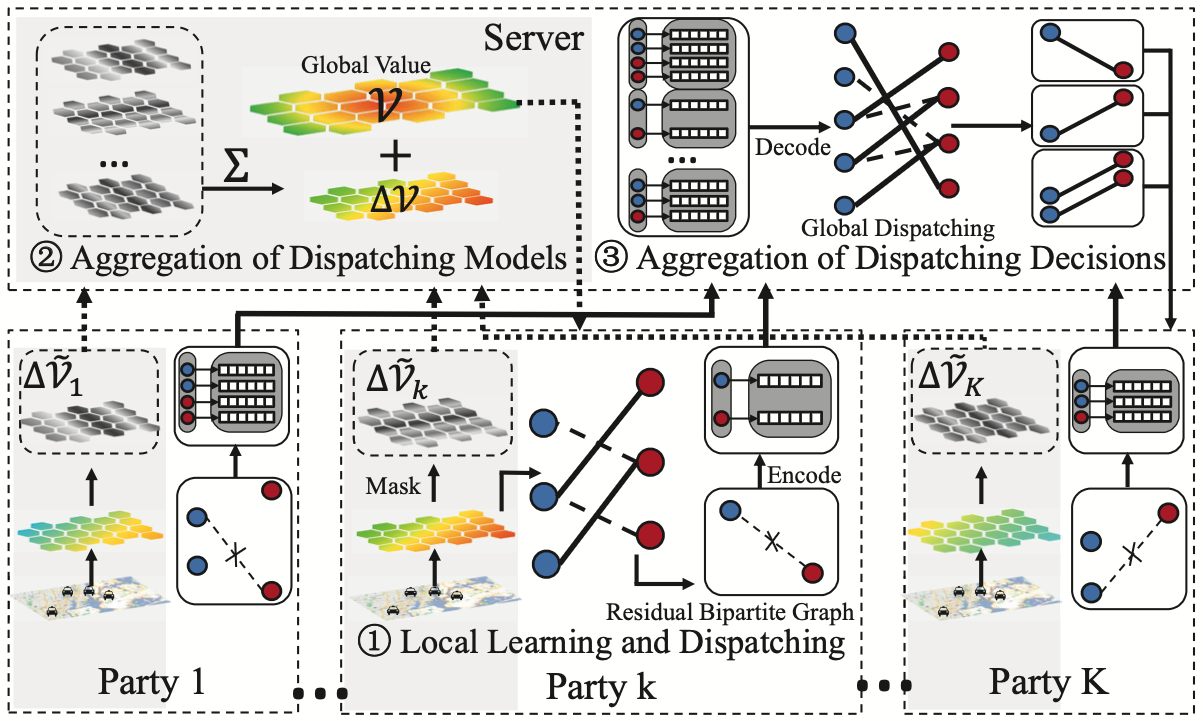
具体在联邦场景下，正如local SGD有其联邦版本FedAvg，这里的基于强化学习的Learning-to-Dispatch(LTD)方法也有其对应的联邦版本Fed-LTD，算法每轮迭代（对应一个批量）的流程可描述如下：

(1) 第\(k\)个client节点执行：

• 更新\(\mathcal{V}_k\):

\[\mathcal{V}_k^{\prime}\left(s^{t}\right) = \mathcal{V}_k\left(s^{t}\right)+\eta \cdot \sum_{u}\left(r_{u}^{t}+\gamma \mathcal{V}_k\left(s_{v}^{t+1}\right)-\mathcal{V}_k\left(s_{u}^{t}\right)\right)

\]

• 计算\(\Delta \mathcal{V}_{k} = \mathcal{V}^{\prime}_{k}-\mathcal{V}_{k}\)。


• 对\(\Delta \mathcal{V}_k\)进行编码：\(
  
  \Delta \widetilde{\mathcal{V}}_k = \text{Encode}(\Delta \mathcal{V}_k)\)。


• 更新边权：
  

  \[w(u, v)=v . r e w a r d+\gamma \mathcal{V}\left(s_{e}^{t+1}\right)-\mathcal{V}\left(s_{u}^{t}\right)
  
  \]

  
  


• 运行匹配算法并得到\(\mathcal{M}(G_k)\)。


• 计算残差二分图\(G_{\Delta_{k}} = G_{k}-\mathcal{M}\left(G_{k}\right)\)。


• 对\(G_{\Delta_{k}}\)进行编码：\(\widetilde{G}_{\Delta_{k}} = \text { EncodeRBG }\left(G_{\Delta_{k}}\right)\)。


• 将\(\Delta \widetilde{\mathcal{V}}_k\)，\(\widetilde{G}_{\Delta_{k}}\)发送到server。

(2) server执行：

• 每\(t_d\)轮聚合一次价值：\(\mathcal{V} = \mathcal{V}+ \sum_{k=1}^{K} \Delta \tilde{\mathcal{V}}_{k}\).


• 对各节点残差二分图进行聚合：\(G_{\Delta} = \operatorname{DecodeRBG}\left(\tilde{G}_{\Delta_{1}}, \cdots \bar{G}_{\Delta_{K}}\right)\)。


• 运行匹配算法得到\(\mathcal{M}^{\prime}(G_{\Delta})\)。


• 将\(\mathcal{V}\)，\(\mathcal{M}^{\prime}(G_{\Delta})\)发往各client节点。

上面的算法描述中对\(\mathcal{\Delta V_k}\)的\(\text{Encode}\)操作为随机掩码(random masking)。其中残差二分图(residual bipartite graph, RBG)\(G_{\Delta_k}\)是指在每一轮迭代进行局部二分图匹配后，每个client剩下的还未匹配的节点。对\(G_{\Delta_k}\)的\(\text{EncodeRBG}\)操作为MD5+局部敏感性哈希(locality sensitive hashing, LSH)， 还函数会生成图节点的安全签名；server则能够通过\(\text{DecodeRBG}\)操作恢复残差二分图。

完整的算法流程示意图如下：

参考

• [1]
  
  Meng C, Rambhatla S, Liu Y. Cross-node federated graph neural network for spatio-temporal data modeling[C]//Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining. 2021: 1202-1211.


• [2] Shi Y, Tong Y, Zeng Y, et al. Efficient Approximate Range Aggregation over Large-scale Spatial Data Federation[J]. IEEE Transactions on Knowledge and Data Engineering, 2021.


• [3] Yansheng Wang, Yongxin Tong, Zimu Zhou, Ziyao Ren, Yi Xu, Guobin Wu, Weifeng Lv. "Fed-LTD: Towards Cross-Platform Ride Hailing via Federated Learning to Dispatch", in Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington D.C., USA, August 14-18, 2022.

数学是符号的艺术，音乐是上界的语言。