立体视觉双目相机立体校正（Bouguet算法）

双目相机立体校正（Bouguet算法）

在双目立体视觉的三维重建过程中，需要通过立体匹配算法来进行视差图的计算得到左右两幅图像的视差值，进而来计算深度来恢复场景的三维信息。

计算三维场景中目标点在左右两个视图上形成的视差，首先要把该点在左右视图上两个对应的像点匹配起来。然而，在二维空间上匹配对应点是非常耗时的，为了减少匹配搜索范围，需要进行双目相机的立体校正，将二维上的匹配搜索降低到一维。

立体校正：把消除畸变后的两幅图像严格地行对应，利用极线约束使得两幅图像的对极线恰好在同一水平线上，这样一幅图像上任意一点与其在另一幅图像上的对应点就必然具有相同的行号，只需在该行进行一维搜索即可匹配到对应点。

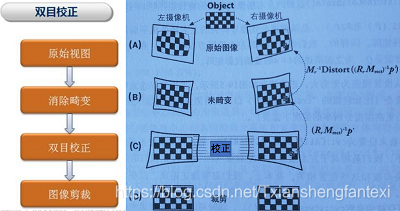
双目校正：是根据摄像头定标后获得的单目内参数据（焦距、成像原点、畸变系数）和双目相对位置关系（旋转矩阵和平移向量），分别对左右视图进行消除畸变和行对准，使得左右视图的成像原点坐标一致、两摄像头光轴平行、左右成像平面共面、对极线行对齐。

• Bouguet立体校正算法

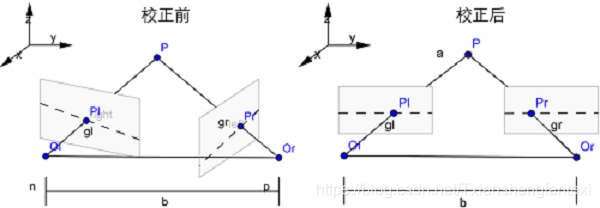
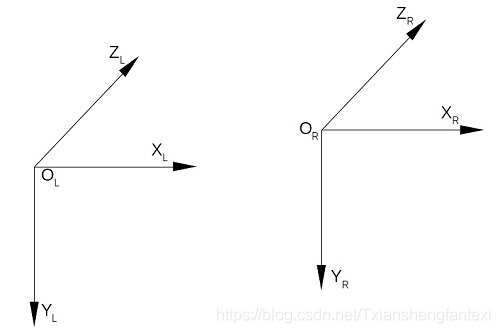
假设通过双目相机的立体标定得到的相机外参为R（向量形式）和T，如下图所示：

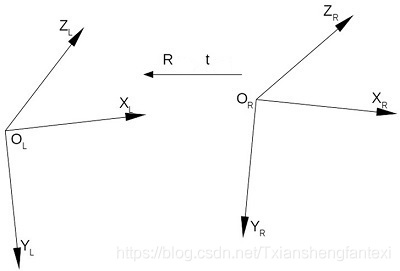
则：(其中：P_l和P_r为同一个世界点分别在左右相机坐标系的三维坐标)

P_l = R*P_r + T;


Bouguet双目立体校正首先是：
1、左相机坐标系沿旋转向量R的正方向旋转一半的R（向量），记该旋转为R_h1（矩阵）；
2、右相机坐标系沿旋转向量R的反方向旋转一半的R（向量），记该旋转为R_h2（矩阵），如下图所示：

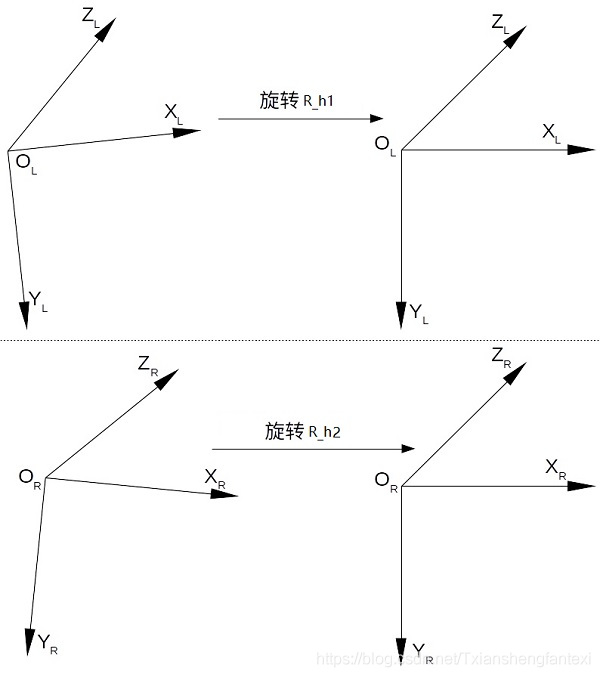
最终得到下图所示：

经过左右相机一半的旋转后，左相机坐标系和右相机坐标系平行但不共面。即，左右相机的x轴、y轴和z轴分别平行，但是左右相机的xoy平面不共面。此时，有：

P_l = P_r + R_h2*T;


令：t = R_h2*T。

然后是：
将平行但不共面的左右相机坐标系旋转（R_rect）至与矫正坐标系（O_rect-X_rect Y_rect Z_rect）平行，使左右相机坐标系平行且共面，如下图所示：

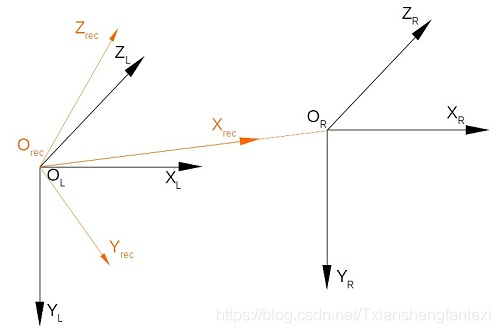
1、矫正坐标系 的 OX 轴 与 左右相机坐标系 原点连线 O_LO_R 平行，其正方向由O_L指向O_R；
2、矫正坐标系 的 XOZ 平面 与 平面 Z_LO_LO_RZ_R 平行，矫正坐标系 的 OY 轴垂直该平面。
3、矫正矩阵 R_rect 的每一列分别对应相机坐标系基轴（单位向量）在矫正坐标系中的投影；而矫正矩阵 R_rect 的每一行分别对应矫正坐标系基轴（单位向量）在相机坐标系中的投影。

• 构造旋转矩阵R_rect
  使得基线与成像平面平行。构造的方法是通过右相机相对于左相机的偏移矩阵T完成的。

1、平移向量t = R_h2*T（单位化后）就是矫正坐标系（O-XYZ）的 OX 轴在相机坐标系中的投影：

r1 = t/||t||;


2、相机坐标系的 O_LZ_L 轴与矫正坐标系的平面 XOZ 平行，矫正坐标系 OY 轴在相机坐标系中的投影为：

r2 = [(0; 0; 1)×t]/||t×(0;0;1)||;


3、矫正坐标系 OZ 轴在相机坐标系中的投影为：

r3 = (r1×r2)/||r1×r2||;


所以，矫正矩阵为：

R_rect = (r1&＃39;; r2&＃39;; r3&＃39;);


最终得到左右相机的旋转矩阵为：

R_L = R_rect*R_h1;
R_R = R_rect*R_h2;


得到左右相机的旋转矩阵之后，即可进行立体校正步骤。

• 立体校正步骤

1、分别将两个图像的像素坐标系通过共同的内参矩阵转换到相机坐标系；
2、分别对两个相机坐标系进行旋转得到新的相机坐标系，通过左乘旋转矩阵R_L逆和R_R逆；(极线约束)
3、针对新的相机坐标分别进行左、右相机的去畸变操作；（畸变校正）
4、去畸变操作结束后，分别用左、右相机的内参矩阵将左、右两个相机坐标系重新转换到左、右图像像素坐标系；
5、并分别用左、右源图像的像素值对新左、右图像的像素点进行插值。

还有一些其他的校正方法，具体在这个链接里面

• Matlab编程代码校正结果