开发笔记:总结所有有关二叉树公共祖先问题

将一棵无穷大满二叉树的结点按根结点一层一层地从左往右编号&＃xff0c;根结点编号为1。现给定a&＃xff0c;b为两个结点。设计一个算法&＃xff0c;返回a、b最近的公共祖先的编号。注意其祖先也可能是结点本身。
测试样例&＃xff1a;
2&＃xff0c;3
返回&＃xff1a;1

链接&＃xff1a;https://www.nowcoder.com/questionTerminal/70e00e490b454006976c1fdf47f155d9
来源&＃xff1a;牛客网

思路

因为是按照0&＃xff0c;1&＃xff0c;2&＃xff0c;3这样的满二叉树&＃xff0c;所以可以直接用公式找到其父亲节点
父亲节点 &＃61; 孩子节点 / 2

找到最低层的那个节点&＃xff0c;然后向上找两个节点的父节点&＃xff0c;判断两者父亲节点是否相同

代码

import java.util.*;
public class LCA {
public int getLCA(int a, int b) {
if(a > b) {
int tmp &＃61; a;
a &＃61; b;
b &＃61; tmp;
}
if(a &＃61;&＃61; b) return a;
//b最大了
while(a !&＃61; b) {
b &＃61; b/2;
if(b < a) {
a &＃61; a/2;
if(a &＃61;&＃61; b) break;
}
}
return a;
}
}

二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为&＃xff1a;“对于有根树 T 的两个结点 p、q&＃xff0c;最近公共祖先表示为一个结点 x&＃xff0c;满足 x 是 p、q 的祖先且 x
的深度尽可能大&＃xff08;一个节点也可以是它自己的祖先&＃xff09;。”

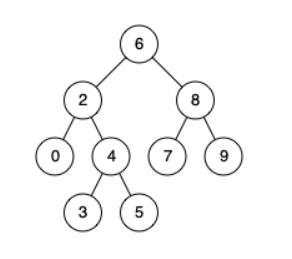
例如&＃xff0c;给定如下二叉搜索树: root &＃61; [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root &＃61; [6,2,8,0,4,7,9,null,null,3,5], p &＃61; 2, q &＃61; 8 输出: 6 解释: 节点 2
和节点 8 的最近公共祖先是 6。 示例 2:

输入: root &＃61; [6,2,8,0,4,7,9,null,null,3,5], p &＃61; 2, q &＃61; 4 输出: 2 解释: 节点 2
和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉搜索树中。

来源&＃xff1a;力扣&＃xff08;LeetCode&＃xff09;
链接&＃xff1a;https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof

思路

若 root.val 若 root.val > p.val&＃xff0c;则 p 在 root 左子树 中&＃xff1b;
若 root.val &＃61; p.val &＃xff0c;则 p 和 root 指向 同一节点 。

代码-遍历

class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while(true) {
if(root.val > p.val && root.val > q.val) {
root &＃61; root.left;
}else if(root.val < p.val && root.val < q.val) {
root &＃61; root.right;
}else break;
}
return root;
}
}


代码-递归

class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root.val < p.val && root.val < q.val)
return lowestCommonAncestor(root.right, p, q);
if(root.val > p.val && root.val > q.val)
return lowestCommonAncestor(root.left, p, q);
return root;
}
}

二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为&＃xff1a;“对于有根树 T 的两个结点 p、q&＃xff0c;最近公共祖先表示为一个结点 x&＃xff0c;满足 x 是 p、q 的祖先且 x
的深度尽可能大&＃xff08;一个节点也可以是它自己的祖先&＃xff09;。”

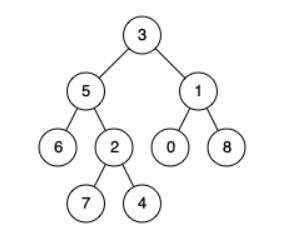
例如&＃xff0c;给定如下二叉树: root &＃61; [3,5,1,6,2,0,8,null,null,7,4]

示例 1:

输入: root &＃61; [3,5,1,6,2,0,8,null,null,7,4], p &＃61; 5, q &＃61; 1 输出: 3 解释: 节点 5
和节点 1 的最近公共祖先是节点 3。 示例 2:

输入: root &＃61; [3,5,1,6,2,0,8,null,null,7,4], p &＃61; 5, q &＃61; 4 输出: 5 解释: 节点 5
和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉树中。

来源&＃xff1a;力扣&＃xff08;LeetCode&＃xff09;
链接&＃xff1a;https://leetcode-cn.com/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof

思路

1. 根节点本身是否是p或者q当中的某个节点
2. 递归根的左和根的右
   2.1 左右两边都不为空&＃xff1a;root是公共祖先
   2.2 左边不为空&＃xff0c;右边为空&＃xff1a;左边第一次找到的节点就是公共祖先
   2.3 左边为空&＃xff0c;右边不为空&＃xff1a;右边第一个节点就是公共祖先
3. 如果都没有&＃xff0c;则返回null

代码-递归

class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root &＃61;&＃61; null) return null;
if(root &＃61;&＃61; q || root &＃61;&＃61; p) return root;
TreeNode left &＃61; lowestCommonAncestor(root.left,p,q);
TreeNode right &＃61; lowestCommonAncestor(root.right,p,q);
if(left !&＃61; null && right !&＃61; null) return root;
if(left !&＃61; null) return left;
if(right !&＃61; null) return right;
return null;
}
}