技术分享：线性回归模型的双路径构建——基于sklearn库的实践探索

导入必要的模块

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error


数据集

x &＃61; np.array([50, 30, 15, 40, 55, 20, 45, 10, 60, 25])
y &＃61; np.array([5.9, 4.6, 2.7, 4.8, 6.5, 3.6, 5.1, 2.0, 6.3, 3.8])


画出数据集的散点图

plt.scatter(x, y)
plt.grid(True)
plt.xlabel(&＃39;area&＃39;)
plt.ylabel(&＃39;price&＃39;)
plt.show()


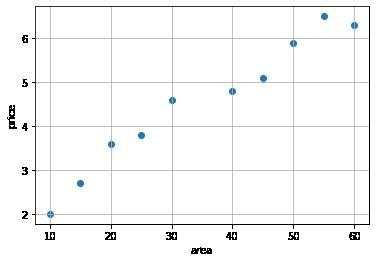
数据划分

划分训练集和测试集

使用到的api&＃xff1a;

数据划分sklearn.model_selection.train_test_split

用到的参数&＃xff1a;

• *arrays&＃xff1a;输入数据集。

• test_size&＃xff1a;划分出来的测试集占总数据量的比例&＃xff0c;取值0~1。

• shuffle&＃xff1a;是否在划分前打乱数据的顺序&＃xff0c;默认True。

• random_state&＃xff1a;shuffle的随机种子&＃xff0c;取值正整数。

返回&＃xff1a;

• splitting&＃xff1a;列表包含划分后的训练集与测试集。

x_train, x_test, y_train, y_test &＃61; train_test_split(
x, y, test_size&＃61;0.3, shuffle&＃61;True, random_state&＃61;23)


查看训练集的散点图

plt.scatter(x_train,y_train)
plt.grid(&＃39;True&＃39;)
plt.xlabel(&＃39;area&＃39;)
plt.ylabel(&＃39;price&＃39;)
plt.show()


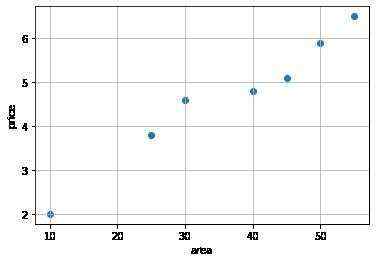
查看测试集的散点图

plt.scatter(x_test,y_test)
plt.grid(&＃39;True&＃39;)
plt.xlabel(&＃39;area&＃39;)
plt.ylabel(&＃39;price&＃39;)
plt.show()


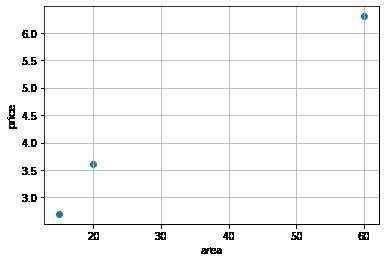
模型搭建

使用到的api&＃xff1a;

线性回归sklearn.linear_model.LinearRegression

model &＃61; LinearRegression()


模型训练

使用到的api&＃xff1a;

线性回归模型训练sklearn.linear_model.LinearRegression.fit

用到的参数&＃xff1a;

• X&＃xff1a;输入特征&＃xff0c;如果输入是np.array格式&＃xff0c;shape必须是(n_sample, n_feature)。

• y&＃xff1a;输入标签。

# x_train的shape由(7,)变为(7,1)
x_train &＃61; x_train.reshape(-1,1)
model.fit(X&＃61;x_train, y&＃61;y_train)


LinearRegression()


模型预测

对测试集做预测

使用到的api&＃xff1a;

线性回归模型预测sklearn.linear_model.LinearRegression.predict

用到的参数&＃xff1a;

• X&＃xff1a;输入特征&＃xff0c;如果输入是np.array格式&＃xff0c;shape必须是(n_sample, n_feature)。

返回&＃xff1a;

• C&＃xff1a;预测结果。

# x_test的shape由(7,)变为(7, 1)
x_test &＃61; x_test.reshape(-1,1)
y_test_pred &＃61; model.predict(x_test)


画出数据集的散点图和预测直线

x_test &＃61; x_test.reshape(-1)
plt.scatter(x_test, y_test, color&＃61;&＃39;g&＃39;, label&＃61;&＃39;test dataset&＃39;)
plt.scatter(x_train, y_train, color&＃61;&＃39;b&＃39;,label&＃61;&＃39;train dataset&＃39;)
plt.plot(np.sort(x_test), y_test_pred[np.argsort(x_test)], color&＃61;&＃39;r&＃39;, label&＃61;&＃39;linear regression&＃39;)
plt.legend()
plt.show()


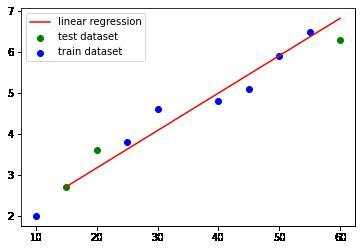
计算评价指标mse

使用到的api&＃xff1a;

均方误差sklearn.metrics.mean_squared_error

用到的参数&＃xff1a;

• y_true&＃xff1a;真实值(ground truth)。

• y_pred&＃xff1a;预测值。

返回&＃xff1a;

• loss&＃xff1a;mse计算结果。

mse &＃61; mean_squared_error(y_true&＃61;y_test, y_pred&＃61;y_test_pred)
print(&＃39;MSE: {}&＃39;.format(mse))


MSE: 0.15383086014546365


查看线性回归模型的系数w和截距b

使用到的api&＃xff1a;

回归系数sklearn.linear_model.LinearRegression.coef_

截距项sklearn.linear_model.LinearRegression.intercept_

w, b &＃61; model.coef_[0], model.intercept_
print(&＃39;Weight&＃61;{0} bias&＃61;{1}&＃39;.format(w, b))


Weight&＃61;0.09139423076923077 bias&＃61;1.3420673076923069