篇首语：本文由编程笔记#小编为大家整理，主要介绍了推荐系统基础:使用PyTorch进行矩阵分解进行动漫的推荐相关的知识，希望对你有一定的参考价值。

我们一天会遇到很多次推荐——当我们决定在Netflix/Youtube上看什么，购物网站上的商品推荐，Spotify上的歌曲推荐，Instagram上的朋友推荐，LinkedIn上的工作推荐……列表还在继续!推荐系统的目的是预测用户对某一商品的“评价”或“偏好”。这些评级用于确定用户可能喜欢什么，并提出明智的建议。

推荐系统主要有两种类型:

基于内容的系统:这些系统试图根据项目的内容(类型、颜色等)和用户的个人资料(喜欢、不喜欢、人口统计信息等)来匹配用户。例如，Youtube可能会根据我是一个厨师的事实，以及/或者我过去看过很多烘焙视频来推荐我烹饪视频，从而利用它所拥有的关于视频内容和我个人资料的信息。

协同过滤:他们依赖于相似用户喜欢相似物品的假设。用户和/或项目之间的相似性度量用于提出建议。

本文讨论了一种非常流行的协同过滤技术——矩阵分解。

矩阵分解

推荐系统有两个实体-用户和物品（物品的范围十分广泛，可以是实际出售的产品，也可以是视频，文章等）。假设有m个用户和n个物品。我们推荐系统的目标是构建一个mxn矩阵(称为效用矩阵)，它由每个用户-物品对的评级(或偏好)组成。最初，这个矩阵通常非常稀疏，因为我们只对有限数量的用户-物品对进行评级。

这是一个例子。假设我们有4个用户和5个超级英雄，我们试图预测每个用户对每个超级英雄的评价。这是我们的评分矩阵最初的样子:

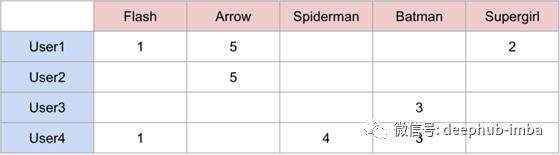
针对超级英雄等级4x5评分矩阵

现在，我们的目标是通过寻找用户和项目之间的相似性来填充这个矩阵。例如，我们看到User3和User4对蝙蝠侠给出了相同的评级，所以我们可以假设用户是相似的，他们对蜘蛛侠的感觉也是一样的，并预测User3会给蜘蛛侠评级为4。然而，在实践中，这并不是那么简单，因为有多个用户与许多不同的项交互。

在实践中，通过将评分矩阵分解成两个高而细的矩阵来填充矩阵。分解得到:

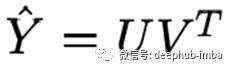
用户-产品对的评分的预测是用户和产品的点积

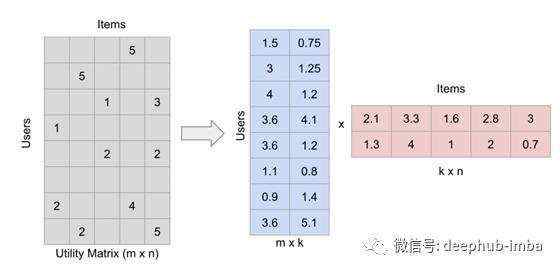
矩阵因式分解(为了方便说明，数字是随机取的)

PyTorch实现

使用PyTorch实现矩阵分解，可以使用PyTorch提供的嵌入层对用户和物品的嵌入矩阵（Embedding）进行分解，利用梯度下降法得到最优分解。

数据集

我使用了来自Kaggle的动画推荐数据集:

https://www.kaggle.com/CooperUnion/anime-recommendations-database

我们有69600个用户和9927个动漫。提供了6337241个评分。

目标

给定一组动画的用户评分，预测每一对用户动画的评分。

数据探索

我们看到有很多评级为-1的行，这表示缺少评级，我们可以去掉这些行。

 anime_ratings_df = pd.read_csv("rating.csv")
 anime_ratings_df.shape
 print(anime_ratings_df.head())

我们还可以查看评分的分布和每个用户的评分数量。

 Counter(anime_ratings.rating)

每个用户的平均评分数

 np.mean(anime_ratings.groupby(['user_id']).count()['anime_id'])

输出 91.05231321839081

数据预处理

因为我们将使用PyTorch的嵌入层来创建用户和物品嵌入，所以我们需要连续的id来索引嵌入矩阵并访问每个用户/项目嵌入。

 def encode_column(column):
    """ Encodes a pandas column with continous IDs"""
    keys = column.unique()
    key_to_id = {key:idx for idx,key in enumerate(keys)}
    return key_to_id, np.array([key_to_id[x] for x in column]), len(keys)
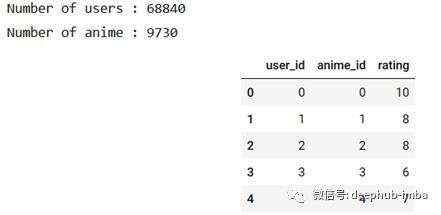
 anime_df, num_users, num_anime, user_ids, anime_ids = encode_df(train_df)
 print("Number of users :", num_users)
 print("Number of anime :", num_anime)
 anime_df.head()

训练

我们的目标是为每个用户和每个物品找到最佳的嵌入向量。然后，我们可以通过获取用户嵌入和物品嵌入的点积，对任何用户和物品进行预测

成本函数：我们目标是使评分矩阵的均方误差最小。这里的N是评分矩阵中非空白元素的数量。

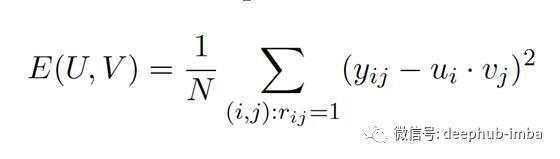
 def cost(df, emb_user, emb_anime):
    """ Computes mean square error"""
    Y = create_sparse_matrix(df, emb_user.shape[0], emb_anime.shape[0])
    predicted = create_sparse_matrix(predict(df, emb_user, emb_anime), emb_user.shape[0], emb_anime.shape[0], 'prediction')
    return np.sum((Y-predicted).power(2))/df.shape[0]

预测

 def predict(df, emb_user, emb_anime):
    """ This function computes df["prediction"] without doing (U*V^T).
     
    Computes df["prediction"] by using elementwise multiplication of the corresponding embeddings and then
    sum to get the prediction u_i*v_j. This avoids creating the dense matrix U*V^T.
    """
    df['prediction'] = np.sum(np.multiply(emb_anime[df['anime_id']],emb_user[df['user_id']]), axis=1)
    return df

用户和物品向量的初始化

有许多方法来初始化嵌入权重，并没有一个统一的答案，例如，fastai使用一种叫做截断标准初始化器（Truncated Normal initializer）的东西。在我的实现中，我刚刚用(0,11 /K)的uniform值初始化了嵌入(随机初始化在我的例子中运行得很好!)其中K是嵌入矩阵中因子的数量。K是一个超参数，通常是由经验决定的——它不应该太小，因为你想让你的嵌入学习足够的特征，但你也不希望它太大，因为它会开始过度拟合你的训练数据，增加计算时间。

 def create_embeddings(n, K):
    """
    Creates a random numpy matrix of shape n, K with uniform values in (0, 11/K)
    n: number of items/users
    K: number of factors in the embedding
    """
    return 11*np.random.random((n, K)) / K

创建稀疏效用矩阵:由于我们的成本函数需要效用矩阵，我们需要一个函数来创建这个矩阵。

 def create_sparse_matrix(df, rows, cols, column_name="rating"):
    """ Returns a sparse utility matrix"""
    return sparse.csc_matrix((df[column_name].values,(df['user_id'].values, df['anime_id'].values)),shape=(rows, cols))

梯度下降

梯度下降方程为：

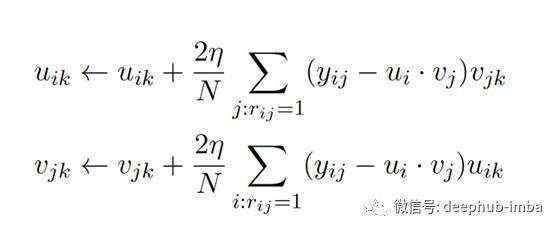
我在实现过程中使用了动量，该动量可以帮助加快相关方向上的梯度下降并抑制振荡，从而加快收敛速度。我还添加了正则化功能，以确保我的模型不会过度适合训练数据。因此，我的代码中的梯度下降方程比上述方程稍微复杂。

正则成本函数为：

 def gradient_descent(df, emb_user, emb_anime, iteratiOns=2000, learning_rate=0.01, df_val=None):
    """
    Computes gradient descent with momentum (0.9) for given number of iterations.
    emb_user: the trained user embedding
    emb_anime: the trained anime embedding
    """
    Y = create_sparse_matrix(df, emb_user.shape[0], emb_anime.shape[0])
    beta = 0.9
    grad_user, grad_anime = gradient(df, emb_user, emb_anime)
    v_user = grad_user
    v_anime = grad_anime
    for i in range(iterations):
        grad_user, grad_anime = gradient(df, emb_user, emb_anime)
        v_user = beta*v_user + (1-beta)*grad_user
        v_anime = beta*v_anime + (1-beta)*grad_anime
        emb_user = emb_user - learning_rate*v_user
        emb_anime = emb_anime - learning_rate*v_anime
        if(not (i+1)%50):
            print("\niteration", i+1, ":")
            print("train mse:", cost(df, emb_user, emb_anime))
            if df_val is not None:
                print("validation mse:", cost(df_val, emb_user, emb_anime))
    return emb_user, emb_anime

在验证集上预测

因为我们无法为我们的训练集中未遇到的用户和动漫（冷启动问题）做出预测，所以我们需要从看不见的数据集中删除它们。

 def encode_new_data(valid_df, user_ids, anime_ids):
    """ Encodes valid_df with the same encoding as train_df.
    """
    df_val_chosen = valid_df['anime_id'].isin(anime_ids.keys()) & valid_df['user_id'].isin(user_ids.keys())
    valid_df = valid_df[df_val_chosen]
    valid_df['anime_id'] = np.array([anime_ids[x] for x in valid_df['anime_id']])
    valid_df['user_id'] = np.array([user_ids[x] for x in valid_df['user_id']])
    return valid_df

我们的模型略微过拟合了训练数据，因此可以增加正则化因子（lambda）以使其更好地泛化。

 train_mse = cost(train_df, emb_user, emb_anime)
 val_mse = cost(valid_df, emb_user, emb_anime)
 print(train_mse, val_mse)

输出：6.025304207874527 11.735503902293352

让我们看看预测：

 valid_df[70:80].head()

鉴于这些评分仅基于用户行为之间的相似性，在1-10的评分范围内，均方根值仅为3.4算是不错了。它显示了即使如此简单，矩阵分解仍然具有多么强大的功能。

矩阵分解的局限性

矩阵分解是一种非常简单和方便的方法。但是，它也有缺陷，其中之一已经在我们的实现中遇到:

冷启动问题

我们无法对训练数据中从未遇到过的项目和用户进行预测，因为我们没有为它们提供嵌入。

冷启动问题可以通过许多方式来解决，包括推荐流行的项目，让用户对一些项目进行评级，使用基于内容的方法，直到我们有足够的数据来使用协同过滤。

很难包含关于用户/物品的附加上下文

我们只使用用户id和物品id来创建嵌入。我们不能在实现中使用关于用户和项的任何其他信息。有一些复杂的基于内容的协同过滤模型可以用来解决这个问题。

评级并不总是可用的

很难从用户那里得到反馈。大多数用户只有在真正喜欢或绝对讨厌某样东西的时候才会给它打分。在这种情况下，我们通常不得不想出一种方法来衡量隐性反馈，并使用负采样技术来想出一个合理的训练集。

结论

推荐系统确实很有趣，但也可能变得太复杂或者太容易，尤其是在有数百万用户和数百万条目的大规模应用中。通常，你可以找到与这些案例研究相对应的研究论文/视频/工程博客。这里有一些有用的资源:

https://developers.google.com/machine-learning/recommendation/collaborative/matrix

https://labs.pinterest.com/user/themes/pin_labs/assets/paper/p2p-www17.pdf

https://static.googleusercontent.com/media/research.google.com/en//pubs/archive/45530.pdf

本文的代码：https://jovian.ml/aakanksha-ns/anime-ratings-matrix-factorization

deephub翻译组