开发笔记:深度学习食用指南

深度学习食用指南

• • 什么是神经网络
  • • 损失函数&＃xff1a;怎么验证神经网络的预测结果
    • • 激活函数&＃xff1a;神经网络的智商怎么蹭的一下就涨了呢
      • 如何计算神经网络的前向传播&＃xff1a;计算权重参数把输入值相加&＃xff0c;再加入偏移值&＃xff0c;形成一个输出值
      • 如何计算神经网络的反向传播&＃xff1a;先计算第N层的变化比例&＃xff0c;再计算第N-1层的&＃xff0c;反向往前推
      • 激活函数的偏导数
      
      
    • 向量化&＃xff1a;人工智能编程和传统编程不一样的地方
    • • [牛刀小试&＃xff1a;识别猫的项目]
      • [牛刀小试&＃xff1a;构建浅层神经网络]
      
      
    • 深层神经网络&＃xff1a;信息技术的核心思想是分层&＃xff0c;用分层解决复杂性
    • • 层次特性&＃xff1a;有关于深度学习内部如何学习的猜想
      • 核对矩阵维度&＃xff1a;如何编程正确的程序
      • 参数和超参数&＃xff1a;神经网络调音师&＃xff0c;要想悦耳如音乐&＃xff0c;就得精准如数学
      • [牛刀小试&＃xff1a;构建深层神经网络]
      
      
    
    
  • 实战基础
  • • 配置数据集
    • 欠拟合和过拟合
    • 正则化
    • dropout
    • 数据增强
    • 梯度消失与梯度爆炸
    • 如何判断网格中有bug
    • H5文件
    • [牛刀小试&＃xff1a;参数初始化]
    • [牛刀小试&＃xff1a;正则化]
    • [牛刀小试&＃xff1a;梯度检验]
    
    
  • 优化算法
  • • mini-batch
    • 指数平均加权
    • 动量梯度下降
    • RMSprop
    • Adam优化算法
    • 学习率衰减
    • 局部最优
    • [牛刀小试&＃xff1a;mini-batch梯度下降]
    • [牛刀小试&＃xff1a;动量梯度下降]
    • [牛刀小试&＃xff1a;Adam]
    • [牛刀小试&＃xff1a;对比不同的优化算法]
    
    
  • 调试神经网络
  • • 为调参选择采样标尺
    • 各种调参经验
    • 调参模式和工具
    • 规范化隐藏层的输入
    • BN的好处
    • softmax
    • [牛刀小试&＃xff1a;Tensorflow实战]
    
    
  • ......
  • 智能视觉
  • • [牛刀小试&＃xff1a;自动驾驶之车辆检测]
    • [牛刀小试&＃xff1a;风格转换]
    • [牛刀小试&＃xff1a;人脸识别]
    • [牛刀小试&＃xff1a;AI换脸]
    
    
  • 语音识别
  • • [牛刀小试&＃xff1a;智能写作]
    • [牛刀小试&＃xff1a;智能音乐]
    • [牛刀小试&＃xff1a;智能作曲]
    • [牛刀小试&＃xff1a;唤醒词检测]
    
    
  • 自然语言处理
  • • [牛刀小试&＃xff1a;类比推理]
    • [牛刀小试&＃xff1a;智能表情]
    • [牛刀小试&＃xff1a;机器翻译]
    
    
  
  

什么是神经网络

• 神经网络

你看一只苍蝇的大脑只有10万个神经元&＃xff0c;能耗那么低&＃xff0c;但是它能看、能飞、能寻找食物&＃xff0c;还能繁殖。而一台的超级计算机&＃xff0c;消耗极大的能量&＃xff0c;有庞大的体积&＃xff0c;可是它的功能为什么还不如一只苍蝇&＃xff1f;

这是因为苍蝇的大脑是高度专业化的&＃xff0c;进化使得苍蝇的大脑只具备这些特定的功能&＃xff0c;而我们的计算机是通用的&＃xff0c;你可以对它进行各种编程&＃xff0c;它理论上可以干任何事情。

这个关键在于&＃xff0c;大脑的识别能力&＃xff0c;不是靠临时弄一些规则临时编程。大脑的每一个功能都是专门的神经网络长出来的&＃xff0c;那计算机能不能效法大脑呢&＃xff1f;

这就给计算机科学家们带来了一些暗示&＃xff1a;

• 大脑是一个强大的模式识别器。人脑非常善于在一个混乱的场景之中识别出你想要的那个东西。比如你能从满大街的人中&＃xff0c;一眼就认出你熟悉的人。
• 大脑的识别功能可以通过训练提高。
• 大脑不管是练习还是使用识别能力&＃xff0c;都不是按照各种逻辑和规则进行的。我们识别一个人脸&＃xff0c;并不是跟一些抽象的规则进行比对。我们不是通过测量这个人两眼之间的距离来识别这个人。我们一眼看过去&＃xff0c;就知道他是谁了。
• 大脑是由神经元组成的。我们大脑里有数百亿个神经元&＃xff0c;大脑计算不是基于明确规则的计算&＃xff0c;而是基于神经元的计算。

这就是神经网络计算做的事情&＃xff0c;而后计算机科学家们就模拟出了一个神经网络。

人类大脑神经元细胞的树突接收来自外部的多个强度不同的刺激&＃xff0c;并在神经元细胞体内进行处理&＃xff0c;将其转化为一个输出结果。如下图所示。

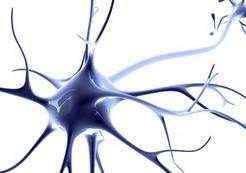
人工神经元也有相似的工作原理。如下图所示。

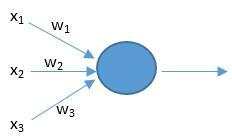
上面的x是神经元的输入&＃xff0c;相当于树突接收的多个外部刺激。w是每个输入对应的权重&＃xff0c;它影响着每个输入x的刺激强度。

假设周末即将到来&＃xff0c;你听说在你的城市将会有一个音乐节。我们要预测你是否会决定去参加。音乐节离地铁挺远&＃xff0c;而且你女朋友想让你陪游。

首先确定影响结果的几个要素&＃xff0c;像天气&＃xff08;天气好不好&＃xff09;、性格&＃xff08;内向或者外向&＃xff09;、兴趣&＃xff08;对音乐的喜欢&＃xff09;&＃xff0c;也就是说有3个因素会影响你的决定&＃xff0c;这3个因素就可以看作是3个输入特征。那你到底会不会去呢&＃xff1f;你的个人喜好——你对上面3个因素的重视程度——会影响你的决定&＃xff0c;这3个重视程度就是3个权重。

如果你觉得地铁远近无所谓&＃xff0c;而且你很喜欢蓝天白云&＃xff0c;那么我们将预测你会去音乐节。这个预测过程可以用我们的公式来表示。

我们假设结果 $z>0$ 的话就表示会去&＃xff0c;小于$0$表示不去。又设偏移值$b\&＃61;-5$。

又设3个特征$(x1,x2,x3)$为$(0,0,1)$&＃xff0c;最后一个是$1$&＃xff0c;它代表了好天气。

又设三个权重$(w1,w2,w3)$是$(2,2,7)$&＃xff0c;最后一个是$7$表示你很喜欢好天气。

那么就有 $z\&＃61;(x1\ast w1\&＃43;x2\ast w2\&＃43;x3\ast w3)\&＃43;b\&＃61;(0\ast 2\&＃43;0\ast 2\&＃43;1\ast 7)\&＃43;(-5)\&＃61;2$。

预测结果 $z\&＃61;2$&＃xff0c;$2>0$&＃xff0c;所以预测你会去音乐节。

如果你本质就是宅&＃xff0c;并且对其它两个因素并不在意&＃xff0c;那么我们预测你将不会去音乐节。

这同样可以用我们的公式来表示。设三个权重$(w1,w2,w3)$是$(2,7,2)$&＃xff0c;w2是7表示你就是特别喜欢呆在家里。

那么就有 $z\&＃61;(x1\ast w1\&＃43;x2\ast w2\&＃43;x3\ast w3)\&＃43;b\&＃61;(0\ast 2\&＃43;0\ast 7\&＃43;1\ast 2)\&＃43;(-5)\&＃61;-3$。

预测结果 $z\&＃61;-3$&＃xff0c;$-3<0$&＃xff0c;所以预测你不会去&＃xff0c;会呆在家里。

神经元的内部参数&＃xff0c;包括权重w和偏移值b&＃xff0c;都是可调的&＃xff08;开始时我们会随机初始化&＃xff09;。用数据训练神经网络的过程&＃xff0c;就是调整更新各个神经元的内部参数的过程。神经网络的结构在训练中不变&＃xff0c;是其中神经元的参数决定了神经网络的功能。

反复学习是刺激神经元&＃xff0c;相当于加大权重的确定程度&＃xff08;不是加大权重的大小&＃xff09;。一开始神经元给这个输入数据的权重是0.9&＃xff0c;但这是一个随机的分配&＃xff0c;有很大的不确定性。随着训练的加深&＃xff0c;神经网络越来越相信这个权重应该是0.11&＃xff0c;参数稳定在这里。数值&＃xff0c;增大或者减小了不重要&＃xff0c;关建是确定性大大增加了。

对比到人&＃xff0c;这就好比篮球&＃xff0c;训练的目的不是让投篮的用力越来越大&＃xff0c;而是越来越准确。

这的确相当于大脑神经元之间的连接越来越稳固&＃xff01;有句话叫 fire together, wire together —— 经常在一起激发的两个神经元会“长”在一起&＃xff0c;它们之间的电信号会更强。但是请注意&＃xff0c;电信号强并不对应参数权重的数值大&＃xff0c;而是对应参数更确定。这就好像发电报汇款&＃xff0c;我收到一个很强很强的汇款信号&＃xff0c;但这只是一笔很小的钱 —— 信号强烈只是确保钱数不会错。

本质上&＃xff0c;神经元做的事情就是按照自己的权重参数把输入值相加&＃xff0c;再加入偏移值&＃xff0c;形成一个输出值。如果输出值大于某个阈值&＃xff0c;我们就说这个神经元被“激发”了。当然&＃xff0c;人脑的神经元不一定是这么工作的&＃xff0c;但是这个模型在计算中很好用。

这就是神经元的基本原理。真实应用中的神经元会在计算过程中加入非线性函数的处理&＃xff0c;并且确保输出值都在 0 和 1 之间&＃xff0c;这个非线性函数被称为激活函数&＃xff0c;记录在下文。

这是单个神经元的计算&＃xff0c;而在我们的大脑中&＃xff0c;有数十亿个称为神经元的细胞&＃xff0c;它们连接成了一个神经网络。

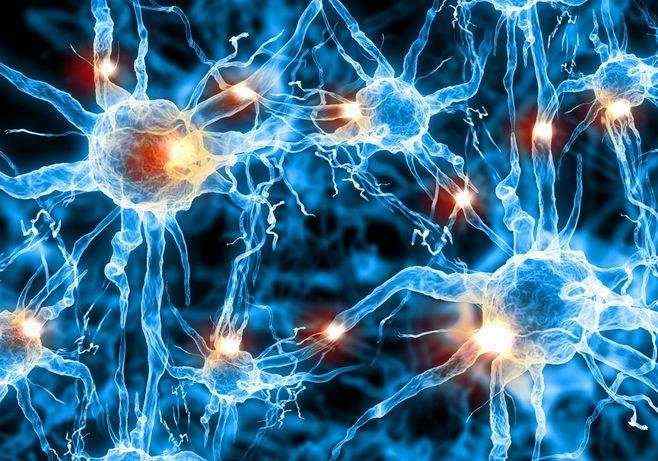
人工神经网络正是模仿了上面的网络结构。下面是一个人工神经网络的构造图。每一个圆代表着一个神经元&＃xff0c;他们连接起来构成了一个网络。

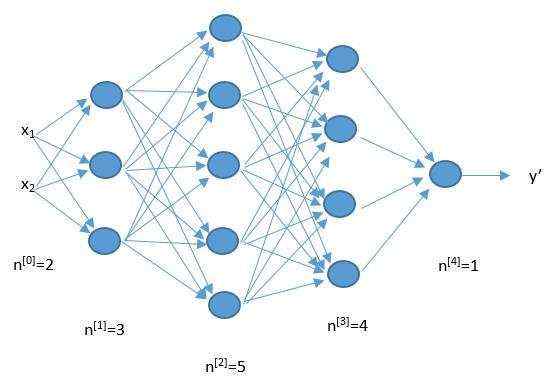
它从左到右分为三层&＃xff0c;每一个圆点代表一个神经元。

• 第一层是“输入层”&＃xff0c;代表输入的数据。
• 第二层叫“隐藏层”&＃xff0c;所谓深度学习就是中间不只有一个隐藏层。
• 第三层是“输出层”&＃xff0c;得到一个输出值。

数据输入进来&＃xff0c;经过隐藏层各个神经元的一番处理&＃xff0c;再把信号传递给输出层&＃xff0c;输出层神经元再处理一番&＃xff0c;最后作出判断。

对于多神经元网络&＃xff0c;拆分看就是一个个单独的神经元&＃xff0c;神经元网络的计算就是重复单神经元的计算。

从下面这张图&＃xff0c;你可以看到它的运行过程。

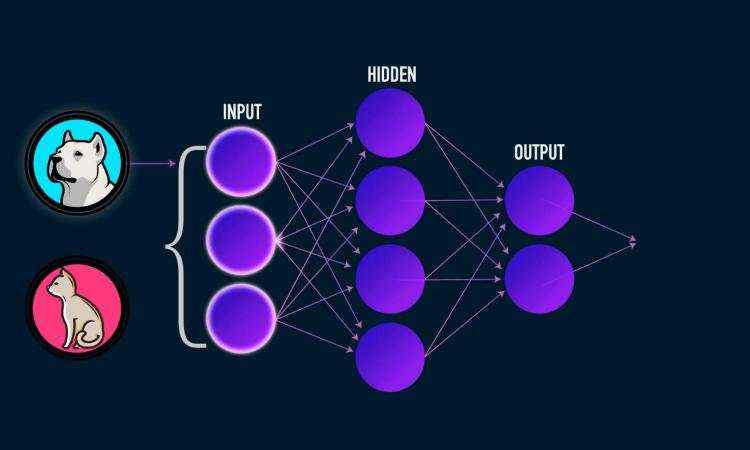
神经网络预测的准确与否&＃xff0c;由权重w和偏移值b决定&＃xff0c;所以神经网络学习的目的就是找到合适的w和b。

任何一个机器学习的过程&＃xff0c;其实都是不断地调整数学模型参数的过程&＃xff0c;直到参数收敛到最佳点。

每一次调整被称为是一次迭代&＃xff0c;调整的幅度被称为迭代的步长。一开始的时候&＃xff0c;迭代的步长要比较大&＃xff0c;这样能够很快地确定大致范围&＃xff0c;效率比较高。

但是&＃xff0c;如果总是把步长设计得很大&＃xff0c;那么最后可能会找不到最佳的参数&＃xff0c;因为要么走过头了&＃xff0c;要么没有走到。因此&＃xff0c;机器学习到最后需要缩小步长&＃xff0c;进行精调&＃xff0c;以保证最后收敛到最佳点。

世界上每年有很多机器学习方面的论文&＃xff0c;都是围绕提高学习效率展开的&＃xff0c;而其中的核心其实就是怎样用最少次迭代&＃xff0c;完成模型的训练——当然&＃xff0c;任何好的机器学习算法都不是事先人为设定步长&＃xff0c;而是在学习的过程中&＃xff0c;自动找到合适的步长。

我们可以通过一种叫梯度下降的搜索方法&＃xff0c;TA会一步步的改变w和b的值&＃xff0c;新的w和b会使损失函数的输出结果更小&＃xff0c;即一步步让预测更加精确。
 

损失函数&＃xff1a;怎么验证神经网络的预测结果

损失函数用来评价模型的预测值和真实值不一样的程度&＃xff0c;损失函数越好&＃xff0c;通常模型的性能越好。

啥意思呢&＃xff1f;我们人类学习同理&＃xff0c;如果一个人一直不停的学&＃xff0c;但是不验证自己的学习成果&＃xff0c;那么有可能学的方向或者学习方法是错误的&＃xff0c;不停的学但结果都白学了。要验证学习成果&＃xff0c;就要判断预测结果是否准确&＃xff0c;损失函数就是做这个的。

不同的模型用的损失函数一般也不一样&＃xff0c;所以损失函数有几种&＃xff0c; $J()、L()$ 。
 

激活函数&＃xff1a;神经网络的智商怎么蹭的一下就涨了呢

神经网络其实就是线性函数&＃xff0c;函数就是一条直线&＃xff0c;能处理的问题也只是线性函数可以处理的问题。

激活函数是非线性函数&＃xff0c;不同的激活函数的样子不同&＃xff0c;可能是曲线等等&＃xff0c;而后就可以让神经网络处理各种问题了。

但这个激活函数用的较少&＃xff0c;一般用改进的 tanh。

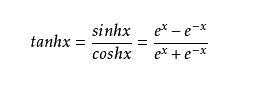
tanh 图像和 sigmoid 的形状是一样的&＃xff0c;只不过整体往下移了一点。

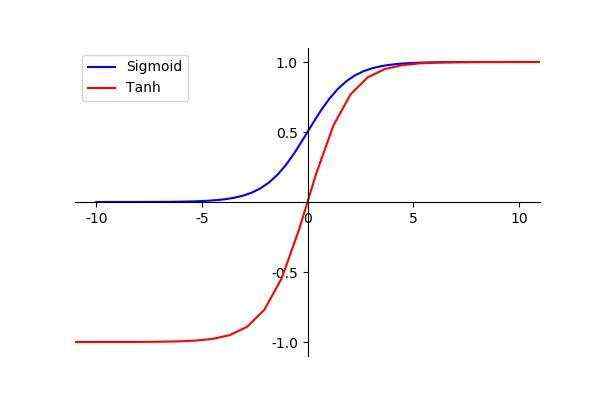
sigmoid 输出值是在 $[0,1]$&＃xff0c;平均值是0.5&＃xff0c;tanh 输出值是在 $[-1,1]$&＃xff0c;平均值是0。

改进就在这里&＃xff0c;将靠近0的输出值传给下层神经网元&＃xff0c;就会更有效。

俩者都有一个不足&＃xff0c;数据大时&＃xff0c;神经网络学习速度就很慢。

学习速度和偏导数大小相关&＃xff0c;偏导数就是斜率&＃xff08;变化比例&＃xff09;&＃xff0c;斜率&＃xff08;变化比例&＃xff09;越大偏导数越大&＃xff0c;学习速度越快。

通过观察俩者的图像发现&＃xff0c;当输入值越来越大时&＃xff0c;曲线的斜率&＃xff08;变化比例&＃xff09;是越来越小的。

为了解决这个问题&＃xff0c;后来创造了relu。

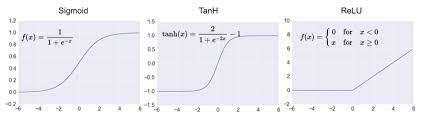
relu 图像&＃xff1a;

• 在输入为正时&＃xff0c;斜率&＃xff08;变化比例&＃xff09;很大。
• 在输入为负时&＃xff0c;就会输出 0&＃xff0c;神经元就不会被激活 — 说明同一时间里&＃xff0c;只有部分神经元会被激活&＃xff0c;从而使得网络很稀疏&＃xff0c;进而计算更高效&＃xff0c;但没有斜率&＃xff08;变化比例&＃xff09;。

为了解决没有斜率&＃xff08;变化比例&＃xff09;的问题&＃xff0c;又创造了一种激活函数&＃xff1a;leaky relu。

leaky relu 的优点将 0 的梯度去掉&＃xff0c;换成一个非0的梯度&＃xff0c;比如0.1等&＃xff0c;这样把0梯度变成一个很小不为0的梯度。

sigmoid 类的激活函数&＃xff0c;只可以处理二元分类问题&＃xff0c;神经网络只能判断是或否。

softmax 可以让神经网络的预测更加丰富&＃xff0c;从二元判断到多元判断。

比如&＃xff0c;之前只能用来判断图中有木有猫&＃xff0c;现在可以同时判断出猫、狗、鸡。

常用的激活函数&＃xff1a;

• sigmoid&＃xff1a;特别适用于&＃xff0c;二元分类的输出层&＃xff0c;其他方面不如tanh
• tanh&＃xff1a;sigmoid改进
• relu&＃xff1a;首选&＃xff0c;用的最多&＃xff0c;但只在隐藏层使用
• leaky relu&＃xff1a;relu改进
• softmax&＃xff1a;N元分类的输出层&＃xff0c;输出层神经元要有N个

如何计算神经网络的前向传播&＃xff1a;计算权重参数把输入值相加&＃xff0c;再加入偏移值&＃xff0c;形成一个输出值

如何计算神经网络的反向传播&＃xff1a;先计算第N层的变化比例&＃xff0c;再计算第N-1层的&＃xff0c;反向往前推

激活函数的偏导数

向量化&＃xff1a;人工智能编程和传统编程不一样的地方

假设您已经有了Python基础。

人工智能编程和传统编程不一样的地方&＃xff0c;在于训练一个智能模型需要非常多的数据&＃xff0c;计算量很大&＃xff0c;需要很长的时间&＃xff0c;所以我们会向量化&＃xff0c;来提高计算速度。

“向量化”(简化)是重写一个循环的过程&＃xff0c;这样它可以不处理数组N次的单个元素&＃xff0c;而是同时处理(比方说)数组的4个元素N/4次。

传统编程&＃xff1a;

for(int i&＃61;0; i<10000; i&＃43;&＃43;)
a[i] &＃61; 1


向量化&＃xff1a;

for(int i&＃61;0; i<10000; i&＃43;&＃43;){
a[i] &＃61; 1; a[i&＃43;1] &＃61; 1; a[i&＃43;2] &＃61; 1; a[i&＃43;3]&＃61;1;
i &＃61; i &＃43; 4;
}


判断和赋值就减少了





3


4




\\frac{3}{4}


43​。

因为现在的CPU都有“向量”或“SIMD”指令集&＃xff0c;它们同时对两个、四个或多个数据进行相同的操作。如果使用 for 循环&＃xff0c;那一条指令的for循环里并没有使用并行计算&＃xff0c;也就没有充分利用计算机的资源。

举个例子&＃xff0c;





∑



i


&＃61;


1



3




a


i



∗



b


i




\\sum\\limits_{i&＃61;1}^3 a_{i} * b_{i}


i&＃61;1∑3​ai​∗bi​。

传统编程&＃xff1a;

a &＃61; b &＃61; [1, 2, 3]
ans &＃61; 0
for x in range(0, 3):
ans &＃61; a[i] &＃43; b[i]


向量化&＃xff1a;

import numpy as np
a &＃61; b &＃61; [1, 2, 3]
np.dot(a, b)
# dot函数是如何对矩阵进行运算&＃xff0c;里面的代码是用C语言实现的&＃xff0c;比Python自身实现的要快得多
# 如果是向量&＃xff0c;返回的是两向量的点乘&＃xff1a;A*B &＃61; A1*B1 &＃43; A2*B2 ··· &＃43;An*Bn&＃xff08;需要检查边界&＃xff1a;俩个向量维度相等&＃xff09;&＃xff0c;结果是一个数
# 如果是矩阵&＃xff0c;返回的是俩矩阵的乘积&＃xff1a;矩阵乘法内容&＃xff0c;&＃xff08;需要检查边界&＃xff1a;乘号前的矩阵的列数要等于后面矩阵的行数&＃xff09;&＃xff0c;结果是一个矩阵


扩展知识&＃xff1a;向量、矩阵。

基本上&＃xff0c;我们每个算法里都会想怎么向量化。

def sigma(x):
return 1 / ( 1 &＃43; pow(e, x) )
z &＃61; a &＃61; y &＃61; dz &＃61; []
for i in range(1, m): # 遍历所有样本
temp &＃61; 0
for j in range(1, n): # 遍历样本里的输入特征
temp &＃43;&＃61; w[j] * x[i][j]

z[i] &＃61; temp &＃43; b # 输出值z &＃61; 权重 &＃43; 偏移值
a[i] &＃61; sigma (z[i]) # 每一个神经元得出的z都需要通过激活函数变成激活值/预测值a
J &＃43;&＃61; -( y[i] * log(a[i]) &＃43; (1 - y[i]) * log(1 - a[i]) ) # 通过预测值和真实值构建一个损失函数J来计算损失
dz[i] &＃61; a[i] - y[i] #
for j in range(1, n):
dw[j] &＃43;&＃61; x[i][j] * dz[i]
db &＃43;&＃61; dz[i]
# m是样本数量&＃xff0c;除以m是求平均值
J &＃61; J / m, db &＃61; db / m
for j in range(1, n):
dw[j] &＃61; dw[j] / m


向量化后&＃xff1a;

[牛刀小试&＃xff1a;识别猫的项目]

[牛刀小试&＃xff1a;构建浅层神经网络]

深层神经网络&＃xff1a;信息技术的核心思想是分层&＃xff0c;用分层解决复杂性

层次特性&＃xff1a;有关于深度学习内部如何学习的猜想

核对矩阵维度&＃xff1a;如何编程正确的程序

参数和超参数&＃xff1a;神经网络调音师&＃xff0c;要想悦耳如音乐&＃xff0c;就得精准如数学

[牛刀小试&＃xff1a;构建深层神经网络]

实战基础

配置数据集

欠拟合和过拟合

正则化

dropout

数据增强

梯度消失与梯度爆炸

如何判断网格中有bug

H5文件

[牛刀小试&＃xff1a;参数初始化]

[牛刀小试&＃xff1a;正则化]

[牛刀小试&＃xff1a;梯度检验]

优化算法

mini-batch

指数平均加权

动量梯度下降

RMSprop

Adam优化算法

学习率衰减

局部最优

[牛刀小试&＃xff1a;mini-batch梯度下降]

[牛刀小试&＃xff1a;动量梯度下降]

[牛刀小试&＃xff1a;Adam]

[牛刀小试&＃xff1a;对比不同的优化算法]

调试神经网络

为调参选择采样标尺

各种调参经验

调参模式和工具

规范化隐藏层的输入

BN的好处

softmax

[牛刀小试&＃xff1a;Tensorflow实战]

…

智能视觉

[牛刀小试&＃xff1a;自动驾驶之车辆检测]

[牛刀小试&＃xff1a;风格转换]

[牛刀小试&＃xff1a;人脸识别]

[牛刀小试&＃xff1a;AI换脸]

语音识别

[牛刀小试&＃xff1a;智能写作]

[牛刀小试&＃xff1a;智能音乐]

[牛刀小试&＃xff1a;智能作曲]

[牛刀小试&＃xff1a;唤醒词检测]

自然语言处理

[牛刀小试&＃xff1a;类比推理]

[牛刀小试&＃xff1a;智能表情]

[牛刀小试&＃xff1a;机器翻译]