开发笔记:递归的逻辑——递归关系模型

　　查尔斯·巴贝奇是一名19世纪的英国发明家，也被说成是职业数学家。他曾经发明了差分机——一台能够按照设计者的意图，自动处理不同函数的计算过程的机器。这是一台硕大的、泛着微光的金属机器，包括数以千计加工精密的曲柄和齿轮。他在孤军奋战下造出的这台机器，运算精度达到了6位小数，能够算出好几种函数表。此后的实际运用证明，这种机器非常适合于编制航海和天文方面的数学用表。

　　巴贝奇花费了漫长的一生来改进差分机，先是一种设想，然后是另一种设想。他曾设想用储存数据穿孔卡上的指令进行任何数学运算的可能性，并设想了现代计算机所具有的大多数其他特性。然而这些都超越了他所处的时代——巴贝奇的设想直到电子时代才得以完成——改进版的差分机最终没有变成现实。

　　在一次科技展览会上，年轻而又光彩照人的奥古斯塔·爱达·拜伦看到了被称为“思考机器”的差分机试验品。那一刻，爱达确定了她一生的目标——完成这台精美的机器。接下来的几年里，爱达迅速学会了各种数学知识并拜入巴贝奇门下，终其一生让处理数的差分机变成处理信息的分析机。

　　为了展示机器的威力，爱达曾设计了一个假想的程序，它循环运行，一次迭代的结果将成为下一次迭代的输入，每个函数前后相继，遵循相同的规则，巴贝奇将这个思路称为“机器咬尾巴——团团转”。然而这个程序仅仅存在于爱达的头脑中，直到她去世也没有生产出可以运行这个程序的机器。

　　一个世纪后，爱达的梦想终于变成了现实，她的假想也成为程序员们的一种重要算法——递归。

　　先来看一个表达式：

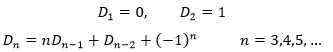
　　表达式指出从第3项开始，每一项都是由前两项通过计算得出的，这类表达式就是递归关系式，有时也称为差分方程。为了能从递归关系式计算出序列中的每一项，必须知道序列开始的若干个数，这些数被称为初始条件或初始值。

　　由于采取逐步计算的方式可以得到序列各项的值，所以很多时候得到递归关系是本身就是朝解决一个计数问题迈了一大步。有些时候甚至只能依赖递归关系进行计算。

　　最著名的递归模型当属斐波那契（Fibonacci）数列，它最早出现在1202年。

　　斐波那契提出了一个关于兔子的问题：某一年的年底将一雄一雌两只兔子放进围场中。从第二年一月份开始，这对兔子生下了一双儿女。此后每一对兔子在第二个月都能产下一对龙凤胎。一年后，围场里能有多少对兔子？

　　这里的假定条件是不考虑兔子的近亲繁殖问题，也不考虑人类吃货造成的影响，并且每对兔子都能健康成长……简单而言就是不考虑科普，只关注数学模型。

递归表达

　　在上一年12月放入一对兔子，次年一月，初始兔子将产下一对新兔子，所以一月份将有两对兔子。二月份，新兔子还没有长大，只有初始兔子能够生产一对兔子，因此二月底将有3对兔子。三月份，初始兔子和1月份诞生的新兔子都将生产一对兔子，再加上二月底本来就有的3对兔子，因此三月底将有2+3=5对兔子：

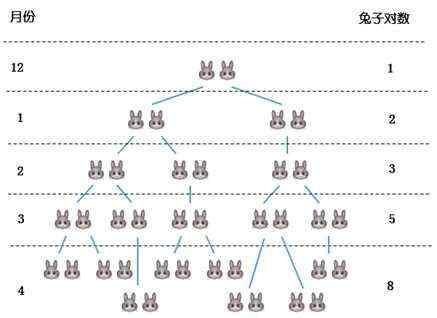
　　如果令f(n)表示第n-1月末围场中的兔子总对数，那么可以总结出：

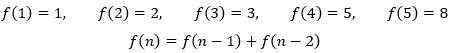
　　可以利用这个关系计算出一年后的兔子总对数，即f(13)，这需要知道f(1)到f(12)的值：

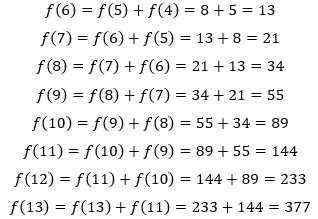
　　一年后围场中有377对兔子。

　　程序通常是从0开始的，因此我们可以令f(0) = 1，这就使得f(2)也满足f(n)的表达式，f(2)=f(1)+f(0)，f(0),f(1),f(2),……,f(n)满足递归关系：

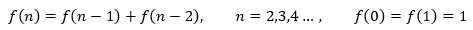
　　这个序列就是著名的斐波那契序列，f(0)和f(1)是序列的初始值。

　　知道了关系模型后很容易写出一段“机器咬尾巴”的代码：

　　打印结果：

避免无用功

　　斐波那契的递归代码很优美，它能够让人以顺序的方式思考，然而这段代码只能作为递归程序的演示样品，并不能应用于实践。在运行时便会发现，当输入大于30时速度会明显变慢，普通家用机甚至无法计算出f(50)。变慢的关键在于每次计算f(n)都要重新求解f(n)前面的所有斐波那契数，相当于做了大量的无用功。

　　知道症结后便可以对症下药，只要把所有计算过的数存储起来就能有效改进算法：

　　全局变量fabo_list将缓存所有计算过的值，这次可以快速计算f(40)~f(50)的值：

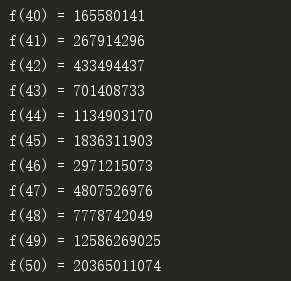
用循环代替递归

　　所有的递归都可以用循环代替，因此递归的实现往往也有对应的循环版本，斐波那契序列也是如此：

　　这段代码的运行速度相当快，不仅预存储了所有计算过的斐波那契数，还比fabo_2省去了因递归导致的方法调用的时间。

　　所有的递归都可以用循环代替，反过来也一样，所有循环也可以用递归代替，像Erlang这种编程语言，甚至没有定义while、for这种用于循环的语法，全部使用递归。

斐波那契序列的和

　　斐波那契序列有很多有趣的性质，其中一个就是求和。

　　用S(n)表示前n项的和：

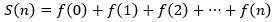
　　先来看一下S(3)，利用f(1) = 1，S(3)可以转换为：

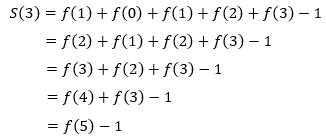
　　由此可以大胆地推断：

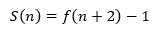
　　可以用数学归纳法证明这个结论：

　　当n=1时，该结论S(1)=f(3)-1=3-1=2，f(0)+f(1)=2，此时结论正确；

　　假设结论对于n=t-1成立，t是任意自然数：

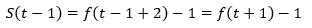
　　则当n=t时：

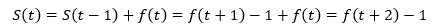
　　由此可见结论是对的，它可以回答图中一共绘制了多少对兔子。

　　求和的代码相当简单，不需要傻乎乎的去累加：

　　下一篇：递归关系的基本解法

　　 作者：我是8位的