作者：浪奔西安 | 来源：互联网 | 2023-09-13 18:39
篇首语：本文由编程笔记#小编为大家整理，主要介绍了Java程序员能看的懂算法复杂度分析：大O符号你都搞不懂，所以只能搬砖到秃顶？相关的知识，希望对你有一定的参考价值。如果
篇首语：本文由编程笔记#小编为大家整理，主要介绍了Java程序员能看的懂算法复杂度分析：大O符号你都搞不懂，所以只能搬砖到秃顶？相关的知识，希望对你有一定的参考价值。
如果你连算法复杂度分析都不会，或者没有这种意思，你学各种排序算、查找等算法有何用，因为你根本不知道或者没有意识什么时候应该使用它。当然，好处还是有的，能提高面试通过机率。
时间复杂度
大O符号背后的思想
大O符号是我们用来讨论算法运行所需时间的语言，用来表示我们如何比较不同方法解决问题的效率。
它就像数学，只是它是一种令人敬畏的、又不枯燥的数学，对于细节东西你可以挥一挥衣袖，而专注于正在发生的事情。
使用大O符号，我们可以通过以下方式表示运行时—当输入变得任意大时，它相对于输入的增长率。
我们来分析一下：
- 运行时增长率—很难确定算法的确切运行时间。 这取决于处理器的速度，计算机还在运行什么等等。因此，我们不是直接讨论运行时间，而是使用大O表示法来讨论运行时增长率。
- 相对输入—由于我们正在衡量运行时增长率，因此我们需要以其他方式表达我们的速度。对于大O符号，输入的大小，称之为“n”。所以可以这么说，运行时间的增长是“按照输入的大小的顺序”(O(n))或者“按照输入大小的平方的顺序”(O(
))。
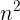- 当输入变得任意大时—n很小的时候，我们的算法可能会有一些步骤看起来很昂贵，但是当n变得很大的时候，我们的算法最终会被其他步骤所掩盖。对于大O分析，我们最关心的是那些随着输入的增长而增长最快的因素，因为当n变得非常大时，其他所有因素都会接近消失。(如果你知道渐近线是什么，你可能会理解为什么“大O分析”有时被称为“渐近线分析”。)
如果你认为这看起来太抽象了，好吧，确实是如此。下面通过一些例子来更加形象的理解。
示例说明
public static void printFirstItem(int[] items) {
System.out.println(items[0]);
}
以上代码，相对于其输入，此方法在O(1)时间（“常数阶”）中运行，输入数组长度可以是1或1000，但是这个方法仍然只需要一个步骤就执行结束，因为始终返回数组的第一个值。
public static void printAllItems(int[] items) {
for (int item : items) {
System.out.println(item);
}
}
以上代码，该方法在O(n)时间(“线性阶”)内运行，其中n是数组中的项数或者长度。如果数组有10项，就要打印10次，如果它有1000项，就要1000次。
public static void printAllPossibleOrderedPairs(int[] items) {
for (int firstItem : items) {
for (int secondItem : items) {
System.out.println(firstItem + ", " + secondItem);
}
}
}
以上代码，这里我们嵌套了两个循环，如果我们的数组有n项，那么外层循环运行n次，而内层循环每次循环运行n次，总共输出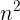次。因此，该方法在O(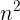)时间内运行(或“二次方时间”)。如果数组有10项，就要打印100次。如果有1000项，就要打印100万次。
N可以是实际的输入项，或者输入的大小
这两种方法都是O(n)运行时间，尽管一个以整数作为输入，另一个以数组作为输入：
public static void sayHiNTimes(int n) {
for (int i = 0; i System.out.println("hi");
}
}
public static void printAllItems(int[] items) {
for (int item : items) {
System.out.println(item);
}
}
因此，有时n是作为方法输入的实际数字或大小，有时n是一个输入数组(或一个map、或一个object等)中的项数。
省略常数
这是大O符号的规则之一，当你计算某个任务的大O复杂度时，要护额略常数，如：
public static void printAllItems(int[] items) {
for (int item : items) {
System.out.println(item);
}
}
public static void printAllItemsTwice(int[] items) {
for (int item : items) {
System.out.println(item);
}
上面这段代码的时间复杂度是O(2n)，但我们也叫它O(n)。
public static void printFirstItemThenFirstHalfThenSayHi100Times(int[] items) {
System.out.println(items[0]);
int middleIndex = items.length / 2;
int index = 0;
while (index System.out.println(items[index]);
index++;
}
for (int i = 0; i <100; i++) {
System.out.println("hi");
}
}
上面这段代码的时间复杂度是O(1+n/2+100) ，我们也叫它O(n)。
为什么我们能这么理解呢？记住，对于大O符号，我们考虑的是当n趋于无穷大时会发生什么。当n变得越来越大，甚至趋于无穷大时，加100或除以2的效果可以忽略不计。
只保留增长最快的项
public static void printAllNumbersThenAllPairSums(int[] numbers) {
System.out.println("these are the numbers:");
for (int number : numbers) {
System.out.println(number);
}
System.out.println("and these are their sums:");
for (int firstNumber : numbers) {
for (int secondNumber : numbers) {
System.out.println(firstNumber + secondNumber);
}
}
}
这里运行时间是O(n+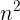)，大O也就是O(
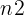)，即使它是O(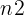/2+100n) ，大O表示仍然是O()。
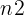类似的：
- O(
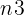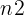+ 50 + 10000) 大O表示是 O()
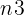- O((n + 30) * (n + 5)) 大O表示是 O()
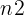这是大O符号的规则之二，几项之和我们只保留增长最快（通常是阶最高）的项，其他项省略。
只讨论最坏的情况
通常这种“最坏情况”条件是隐含的，但是如果你明确地说出来，会给面试官留下更深刻的印象。
因为有时最坏的情况要比最好的情况严重得多：
public static boolean contains(int[] haystack, int needle) {
以上的代码中，我们的haystack中可能有100个项，但是第一个项可能是想要needle，在这种情况下，我们只需要循环一次就能将结果返回。
但实际上，我们会说运行时间是O(n)，这是“最坏情况”。更具体些，我们可以说最坏情况是O(n)和最好情况是O(1)。对于某些算法，我们还可以取“平均情况”的运行时间。
空间复杂度
有时，我们希望优化使用更少的内存，而不是运行更少的时间。讨论内存成本(或“空间复杂度”)与谈论时间成本非常相似，
我们只需查看正在分配的任何新变量的总大小(相对于输入的大小)。
下面这个方法占用O(1)空间(变量只占用一个内存空间)：
public static void sayHiNTimes(int n) {
for (int i = 0; i System.out.println("hi");
}
}
下面这个方法占用O(n)空间(hiArray是数组，随着n的输入分配相应的内存空间)：
public static String[] arrayOfHiNTimes(int n) {
String[] hiArray = new String[n];
for (int i = 0; i hiArray[i] = "hi";
}
return hiArray;
}
通常当我们谈论空间复杂度，我们谈论的是额外的空间，所以不包括输入占用的空间。例如，即使输入有n项，该方法仍然占用常数空间:：
public static int getLargestItem(int[] items) {
int largest = Integer.MIN_VALUE;
for (int item : items) {
if (item > largest) {
largest = item;
}
}
return largest;
}
![技术图片]()
![技术图片]( "点击并拖拽以移动")
有时候在节省时间和节省空间之间会有一个权衡，所以得决定你要优化哪一个。
总结
当然，大O的不只是文中提到两种，本文不讨论大O各个函数阶或者渐进符号。实际程序员面试常遇到最多用到这几种函数阶：
符号 |
名称 |
O(1) |
常数阶 |
O(n) |
线性阶 |
O( ) |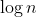
对数阶 |
O(n) |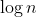
对数线性阶 |
O( ) |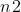
平方阶 |
你应该养成在设计算法时考虑时间和空间复杂性的习惯。不久之后，这将成为你的固性思维，是你在编码时能够立即看到潜在的性能问题与待优化的问题。
渐进分析是一种强大的工具，但要理性地使用它。
大O分析忽略常数，但有时候常数的影响很重要。如果我们有一个需要5个小时运行的脚本，那么将运行时间除以5的优化可能不会影响大O，但它仍然会为你节省4个小时的等待时间。
谨慎过早的优化，有时过早优化时间或空间会对代码可读性或编码消耗时间带来负面影响。对于一个年轻的初创公司来说，编写易于快速发布或对以后易于理解的代码可能更重要，即使算法时间和空间效率要被降低。国内互联网产品基本都是这个思路，就是先快速野蛮生长，任何问题等遇到了或者有足够人力时间剩余了再去优化，当然这个优化不只包括编码，还有比如政策（钻政策漏洞的，可能做大了会被相关机构部门注意到）、盈利模式（先烧资本的钱占领市场再去考虑盈利）等。
但这并不意味着初创公司不关心大O分析，一个优秀有经验的程序员一般会知道如何在运行时间、空间、编码实现时间、可维护性和可读性之间取得适当的平衡。
所以，作为程序员，你应该培养观察出时间和空间优化的技能，以及判断这些优化是否值得进行的思维。
推荐：网站交互设计的特点
南宁SEO（优化推广技术）
京公网安备 11010802041100号