二、聚类算法分类
1.基于划分
给定一个有N个元组或者纪录的数据集&＃xff0c;分裂法将构造K个分组&＃xff0c;每一个分组就代表一个聚类&＃xff0c;K
算法&＃xff1a;K-MEANS算法、K-MEDOIDS算法、CLARANS算法
2.基于层次
对给定的数据集进行层次似的分解&＃xff0c;直到某种条件满足为止。具体又可分为“自底向上”和“自顶向下”两种方案。
特点&＃xff1a;较小的计算开销。然而这种技术不能更正错误的决定。
算法&＃xff1a;BIRCH算法、CURE算法、CHAMELEON算法
3.基于密度
只要一个区域中的点的密度大过某个阈值&＃xff0c;就把它加到与之相近的聚类中去。
特点&＃xff1a;能克服基于距离的算法只能发现“类圆形”的聚类的缺点。
算法&＃xff1a;DBSCAN算法、OPTICS算法、DENCLUE算法
4.基于网格
将数据空间划分成为有限个单元&＃xff08;cell&＃xff09;的网格结构,所有的处理都是以单个的单元为对象的。
特点&＃xff1a;处理速度很快&＃xff0c;通常这是与目标数据库中记录的个数无关的&＃xff0c;只与把数据空间分为多少个单元有关。
算法&＃xff1a;STING算法、CLIQUE算法、WAVE-CLUSTER算法
---------------------
算法步骤及代码实现
1. K-Means(K均值)聚类
算法步骤&＃xff1a;
(1) 首先我们选择一些类/组&＃xff0c;并随机初始化它们各自的中心点。中心点是与每个数据点向量长度相同的位置。这需要我们提前预知类的数量(即中心点的数量)。
(2) 计算每个数据点到中心点的距离&＃xff0c;数据点距离哪个中心点最近就划分到哪一类中。
(3) 计算每一类中中心点作为新的中心点。
(4) 重复以上步骤&＃xff0c;直到每一类中心在每次迭代后变化不大为止。也可以多次随机初始化中心点&＃xff0c;然后选择运行结果最好的一个。
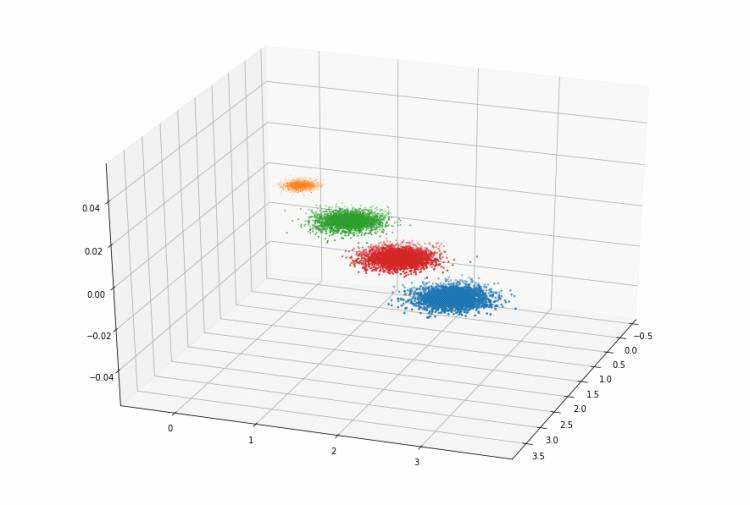
下图演示了K-Means进行分类的过程&＃xff1a;
---------------------
优点&＃xff1a;
速度快&＃xff0c;计算简便
缺点&＃xff1a;
我们必须提前知道数据有多少类/组。
K-Medians是K-Means的一种变体&＃xff0c;是用数据集的中位数而不是均值来计算数据的中心点。
K-Medians的优势是使用中位数来计算中心点不受异常值的影响&＃xff1b;缺点是计算中位数时需要对数据集中的数据进行排序&＃xff0c;速度相对于K-Means较慢。
---------------------
肘部法则
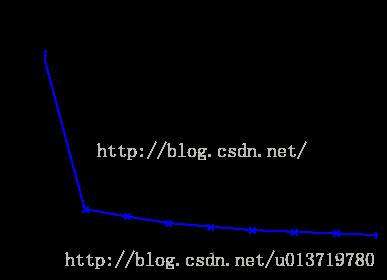
如果问题中没有指定k的值&＃xff0c;可以通过肘部法则这一技术来估计聚类数量。肘部法则会把不同k值的成本函数值画出来。随着kk值的增大&＃xff0c;平均畸变程度会减小&＃xff1b;每个类包含的样本数会减少&＃xff0c;于是样本离其重心会更近。但是&＃xff0c;随着k值继续增大&＃xff0c;平均畸变程度的改善效果会不断减低。k值增大过程中&＃xff0c;畸变程度的改善效果下降幅度最大的位置对应的k值就是肘部。为了让读者看的更加明白&＃xff0c;下面让我们通过一张图用肘部法则来确定最佳的kk值。下图数据明显可分成两类&＃xff1a;
1 import random
2 from sklearn import datasets
3 import numpy as np
4 import matplotlib.pyplot as plt
5 from mpl_toolkits.mplot3d import Axes3D
6 %matplotlib inline
7
8
9 # 正规化数据集 X
10 def normalize(X, axis&＃61;-1, p&＃61;2):
11 lp_norm &＃61; np.atleast_1d(np.linalg.norm(X, p, axis))
12 lp_norm[lp_norm &＃61;&＃61; 0] &＃61; 1
13 return X / np.expand_dims(lp_norm, axis)
14
15
16 # 计算一个样本与数据集中所有样本的欧氏距离的平方
17 def euclidean_distance(one_sample, X):
18 one_sample &＃61; one_sample.reshape(1, -1)
19 X &＃61; X.reshape(X.shape[0], -1)
20 distances &＃61; np.power(np.tile(one_sample, (X.shape[0], 1)) - X, 2).sum(axis&＃61;1)
21 return distances
22
23
24
25 class Kmeans():
26 """Kmeans聚类算法.
27
28 Parameters:
29 -----------
30 k: int
31 聚类的数目.
32 max_iterations: int
33 最大迭代次数.
34 varepsilon: float
35 判断是否收敛, 如果上一次的所有k个聚类中心与本次的所有k个聚类中心的差都小于varepsilon,
36 则说明算法已经收敛
37 """
38 def __init__(self, k&＃61;2, max_iterations&＃61;500, varepsilon&＃61;0.0001):
39 self.k &＃61; k
40 self.max_iterations &＃61; max_iterations
41 self.varepsilon &＃61; varepsilon
42
43 # 从所有样本中随机选取self.k样本作为初始的聚类中心
44 def init_random_centroids(self, X):
45 n_samples, n_features &＃61; np.shape(X)
46 centroids &＃61; np.zeros((self.k, n_features))
47 for i in range(self.k):
48 centroid &＃61; X[np.random.choice(range(n_samples))]
49 centroids[i] &＃61; centroid
50 return centroids
51
52 # 返回距离该样本最近的一个中心索引[0, self.k)
53 def _closest_centroid(self, sample, centroids):
54 distances &＃61; euclidean_distance(sample, centroids)
55 closest_i &＃61; np.argmin(distances)
56 return closest_i
57
58 # 将所有样本进行归类&＃xff0c;归类规则就是将该样本归类到与其最近的中心
59 def create_clusters(self, centroids, X):
60 n_samples &＃61; np.shape(X)[0]
61 clusters &＃61; [[] for _ in range(self.k)]
62 for sample_i, sample in enumerate(X):
63 centroid_i &＃61; self._closest_centroid(sample, centroids)
64 clusters[centroid_i].append(sample_i)
65 return clusters
66
67 # 对中心进行更新
68 def update_centroids(self, clusters, X):
69 n_features &＃61; np.shape(X)[1]
70 centroids &＃61; np.zeros((self.k, n_features))
71 for i, cluster in enumerate(clusters):
72 centroid &＃61; np.mean(X[cluster], axis&＃61;0)
73 centroids[i] &＃61; centroid
74 return centroids
75
76 # 将所有样本进行归类&＃xff0c;其所在的类别的索引就是其类别标签
77 def get_cluster_labels(self, clusters, X):
78 y_pred &＃61; np.zeros(np.shape(X)[0])
79 for cluster_i, cluster in enumerate(clusters):
80 for sample_i in cluster:
81 y_pred[sample_i] &＃61; cluster_i
82 return y_pred
83
84 # 对整个数据集X进行Kmeans聚类&＃xff0c;返回其聚类的标签
85 def predict(self, X):
86 # 从所有样本中随机选取self.k样本作为初始的聚类中心
87 centroids &＃61; self.init_random_centroids(X)
88
89 # 迭代&＃xff0c;直到算法收敛(上一次的聚类中心和这一次的聚类中心几乎重合)或者达到最大迭代次数
90 for _ in range(self.max_iterations):
91 # 将所有进行归类&＃xff0c;归类规则就是将该样本归类到与其最近的中心
92 clusters &＃61; self.create_clusters(centroids, X)
93 former_centroids &＃61; centroids
94
95 # 计算新的聚类中心
96 centroids &＃61; self.update_centroids(clusters, X)
97
98 # 如果聚类中心几乎没有变化&＃xff0c;说明算法已经收敛&＃xff0c;退出迭代
99 diff &＃61; centroids - former_centroids
100 if diff.any() < self.varepsilon:
101 break
102
103 return self.get_cluster_labels(clusters, X)
104
105
106 def main():
107 # Load the dataset
108 X, y &＃61; datasets.make_blobs(n_samples&＃61;10000,
109 n_features&＃61;3,
110 centers&＃61;[[3,3, 3], [0,0,0], [1,1,1], [2,2,2]],
111 cluster_std&＃61;[0.2, 0.1, 0.2, 0.2],
112 random_state &＃61;9)
113
114 # 用Kmeans算法进行聚类
115 clf &＃61; Kmeans(k&＃61;4)
116 y_pred &＃61; clf.predict(X)
117
118
119 # 可视化聚类效果
120 fig &＃61; plt.figure(figsize&＃61;(12, 8))
121 ax &＃61; Axes3D(fig, rect&＃61;[0, 0, 1, 1], elev&＃61;30, azim&＃61;20)
122 plt.scatter(X[y&＃61;&＃61;0][:, 0], X[y&＃61;&＃61;0][:, 1], X[y&＃61;&＃61;0][:, 2])
123 plt.scatter(X[y&＃61;&＃61;1][:, 0], X[y&＃61;&＃61;1][:, 1], X[y&＃61;&＃61;1][:, 2])
124 plt.scatter(X[y&＃61;&＃61;2][:, 0], X[y&＃61;&＃61;2][:, 1], X[y&＃61;&＃61;2][:, 2])
125 plt.scatter(X[y&＃61;&＃61;3][:, 0], X[y&＃61;&＃61;3][:, 1], X[y&＃61;&＃61;3][:, 2])
126 plt.show()
127
128
129 if __name__ &＃61;&＃61; "__main__":
130 main()
2.DBSCAN也是基于密度的聚类算法&＃xff0c;与均值漂移聚类类似
具体步骤&＃xff1a;
1. 首先确定半径r和minPoints&＃xff08;数目&＃xff09;. 从一个没有被访问过的任意数据点开始&＃xff0c;以这个点为中心&＃xff0c;r为半径的圆内包含的点的数量是否大于或等于minPoints&＃xff0c;如果大于或等于minPoints则改点被标记为central point,反之则会被标记为noise point。
2. 重复1的步骤&＃xff0c;如果一个noise point存在于某个central point为半径的圆内&＃xff0c;则这个点被标记为边缘点&＃xff0c;反之仍为noise point。重复步骤1&＃xff0c;知道所有的点都被访问过。
在DBSCAN算法中将数据点分为一下三类&＃xff1a;
核心点&＃xff1a;在半径Eps内含有超过MinPts数目的点
边界点&＃xff1a;在半径Eps内点的数量小于MinPts&＃xff0c;但是落在核心点的邻域内
噪音点&＃xff1a;既不是核心点也不是边界点的点
优点&＃xff1a;不需要知道簇的数量
缺点&＃xff1a;需要确定距离r和minPoints
1 import numpy as np
2
3 from sklearn.cluster import DBSCAN
4 from sklearn import metrics
5 from sklearn.datasets.samples_generator import make_blobs
6 from sklearn.preprocessing import StandardScaler
7
8
9 ##############################################################################
10 # Generate sample data
11 centers &＃61; [[1, 1], [-1, -1], [1, -1]]
12 X, labels_true &＃61; make_blobs(n_samples&＃61;750, centers&＃61;centers, cluster_std&＃61;0.4,
13 random_state&＃61;0)
14
15 X &＃61; StandardScaler().fit_transform(X)
16
17 ##############################################################################
18 # Compute DBSCAN
19 db &＃61; DBSCAN(eps&＃61;0.3, min_samples&＃61;10).fit(X)
20 core_samples_mask &＃61; np.zeros_like(db.labels_, dtype&＃61;bool)
21 core_samples_mask[db.core_sample_indices_] &＃61; True
22 labels &＃61; db.labels_
23
24 # Number of clusters in labels, ignoring noise if present.
25 n_clusters_ &＃61; len(set(labels)) - (1 if -1 in labels else 0)
26
27 print(&＃39;Estimated number of clusters: %d&＃39; % n_clusters_)
28 print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
29 print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
30 print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
31 print("Adjusted Rand Index: %0.3f"
32 % metrics.adjusted_rand_score(labels_true, labels))
33 print("Adjusted Mutual Information: %0.3f"
34 % metrics.adjusted_mutual_info_score(labels_true, labels))
35 print("Silhouette Coefficient: %0.3f"
36 % metrics.silhouette_score(X, labels))
37
38 ##############################################################################
39 # Plot result
40 import matplotlib.pyplot as plt
41
42 # Black removed and is used for noise instead.
43 unique_labels &＃61; set(labels)
44 colors &＃61; plt.cm.Spectral(np.linspace(0, 1, len(unique_labels)))
45 for k, col in zip(unique_labels, colors):
46 if k &＃61;&＃61; -1:
47 # Black used for noise.
48 col &＃61; &＃39;k&＃39;
49
50 class_member_mask &＃61; (labels &＃61;&＃61; k)
51
52 xy &＃61; X[class_member_mask & core_samples_mask]
53 plt.plot(xy[:, 0], xy[:, 1], &＃39;o&＃39;, markerfacecolor&＃61;col,
54 markeredgecolor&＃61;&＃39;k&＃39;, markersize&＃61;14)
55
56 xy &＃61; X[class_member_mask & ~core_samples_mask]
57 plt.plot(xy[:, 0], xy[:, 1], &＃39;o&＃39;, markerfacecolor&＃61;col,
58 markeredgecolor&＃61;&＃39;k&＃39;, markersize&＃61;6)
59
60 plt.title(&＃39;Estimated number of clusters: %d&＃39; % n_clusters_)
61 plt.show()
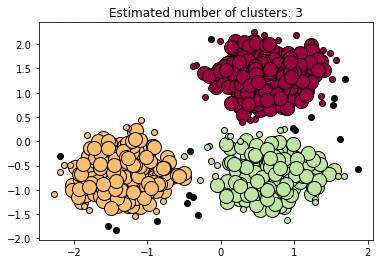
黑色的点代表离群点或者叫噪声点
3.层次聚类
层次聚类算法分为两类&＃xff1a;自上而下和自下而上。凝聚层级聚类(HAC)是自下而上的一种聚类算法。HAC首先将每个数据点视为一个单一的簇&＃xff0c;然后计算所有簇之间的距离来合并簇&＃xff0c;知道所有的簇聚合成为一个簇为止。
度量方法&＃xff1a;
算法步骤&＃xff1a;
1. 首先我们将每个数据点视为一个单一的簇&＃xff0c;然后选择一个测量两个簇之间距离的度量标准。例如我们使用average linkage作为标准&＃xff0c;它将两个簇之间的距离定义为第一个簇中的数据点与第二个簇中的数据点之间的平均距离。
2. 在每次迭代中&＃xff0c;我们将两个具有最小average linkage的簇合并成为一个簇。
3. 重复步骤2知道所有的数据点合并成一个簇&＃xff0c;然后选择我们需要多少个簇。
层次聚类优点&＃xff1a;&＃xff08;1&＃xff09;不需要知道有多少个簇
&＃xff08;2&＃xff09;对于距离度量标准的选择并不敏感
缺点&＃xff1a;效率低
---------------------
1 import numpy as np
2 import pandas as pd
3 from sklearn.cluster import AgglomerativeClustering
4 import matplotlib.pyplot as plt
5 import numpy as np
6 from scipy import ndimage
7 from matplotlib import pyplot as plt
8 from sklearn import manifold, datasets
9
10
11 # In[2]:
12 #1797个样本&＃xff0c;每个样本包括8*8像素的图像和一个[0, 9]整数的标签
13 digits &＃61; datasets.load_digits(n_class&＃61;10)#手写字体数据集,
14 X &＃61; digits.data
15 y &＃61; digits.target
16 n_samples, n_features &＃61; X.shape
17 print(digits.keys())
18 print X[:5,:]
19 print n_samples,n_features
20
21
22 # In[3]:
23
24 # Visualize the clustering
25 def plot_clustering(X_red, X, labels, title&＃61;None):
26 x_min, x_max &＃61; np.min(X_red, axis&＃61;0), np.max(X_red, axis&＃61;0)
27 X_red &＃61; (X_red - x_min) / (x_max - x_min)
28
29 plt.figure(figsize&＃61;(6, 4))
30 for i in range(X_red.shape[0]):
31 plt.text(X_red[i, 0], X_red[i, 1], str(y[i]),
32 color&＃61;plt.cm.spectral(labels[i] / 10.),
33 fontdict&＃61;{&＃39;weight&＃39;: &＃39;bold&＃39;, &＃39;size&＃39;: 9})
34
35 plt.xticks([])
36 plt.yticks([])
37 if title is not None:
38 plt.title(title, size&＃61;17)
39 plt.axis(&＃39;off&＃39;)
40 plt.tight_layout()
41
42
43 # In[ ]:
44
45 # 2D embedding of the digits dataset
46 print("Computing embedding")
47 X_red &＃61; manifold.SpectralEmbedding(n_components&＃61;2).fit_transform(X)
48 print("Done.")
49
50 from sklearn.cluster import AgglomerativeClustering
51
52 for linkage in (&＃39;ward&＃39;, &＃39;average&＃39;, &＃39;complete&＃39;):
53 clustering &＃61; AgglomerativeClustering(linkage&＃61;linkage, n_clusters&＃61;10)
54 clustering.fit(X_red)
55 plot_clustering(X_red, X, clustering.labels_, "%s linkage" % linkage)
56
57
58 plt.show()
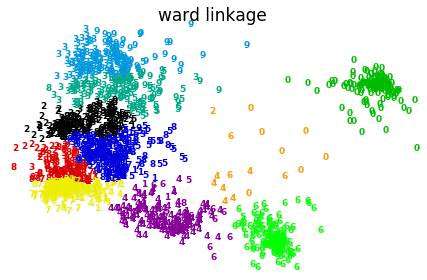
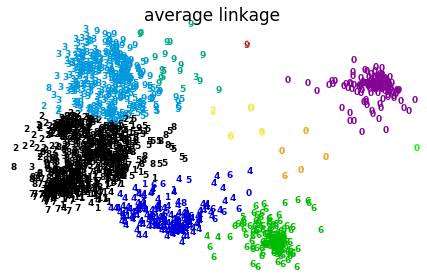
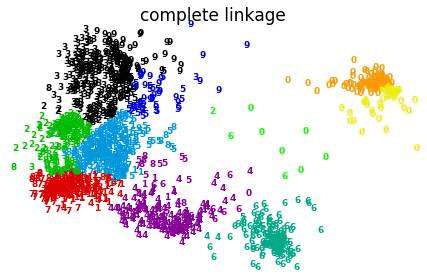
上图显示层次聚类采用不同距离度量方法的效果&＃xff0c;complete在此数据集上效果较差。
京公网安备 11010802041100号