计算摄影——图像去噪（一）

        这一章来整理下图像去噪相关的内容&＃xff0c;主要包括&＃xff1a;噪声类型&＃xff0c;评估方法&＃xff0c;传统去噪方法&＃xff0c;深度学习去噪方法&＃xff0c;常用数据集&＃xff0c;这一章主要讲前三部分。

噪声类型

        摄影中的噪声主要有3种&＃xff1a;固定噪声、随机噪声、非均匀响应噪声。

        固定噪声&＃xff1a;这种噪声来自电路本身&＃xff0c;在各类信号处理系统中广泛存在&＃xff0c;信噪比&＃xff08;signal no noise ratio, SNR&＃xff09;曲线是一条斜率为20dB/dec的直线&＃xff0c;20dB代表信号幅度是噪声信号幅度的10倍&＃xff0c;此时信号能够比较好的保证质量。

        随机噪声&＃xff1a;光子进入传感器的过程在数学上可以用泊松分布进行建模&＃xff0c;此时带来的噪声是与亮度的平方根成正比的&＃xff0c;信噪比曲线是一条斜率为10dB/dec 的直线。

        非均匀响应噪声&＃xff1a;这种噪声来源于每个像素在制造时候的个体差异&＃xff0c;即使感受相同的亮度&＃xff0c;不同像素给出的响应也是不同的&＃xff0c;它的信噪比是一条水平线&＃xff0c;它决定了相机信噪比的上限。

评估方法

        常用的客观评估标准包括峰值信噪比&＃xff08;PSNR&＃xff09;和结构一致性相似因子&＃xff08;SSIM&＃xff09;

PSNR&＃xff1a;

        这是原图像与处理图像之间均方误差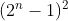&＃xff08;MSE&＃xff09;相对于的对数值&＃xff0c;其中n是每个采样值的位数&＃xff0c;8位图像即256&＃xff0c;PSN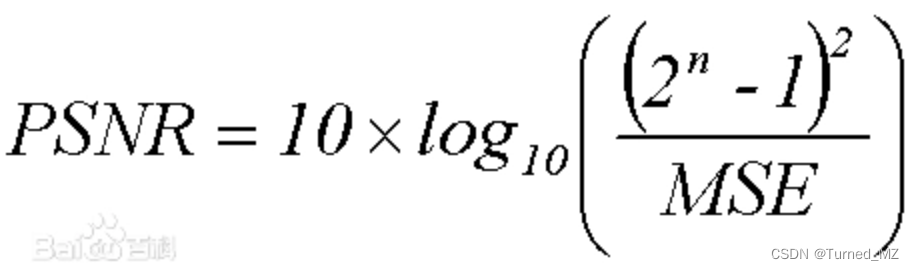R定义如下&＃xff1a;&＃xff0c;PSNR越大表示失真越小。MSE的计算如下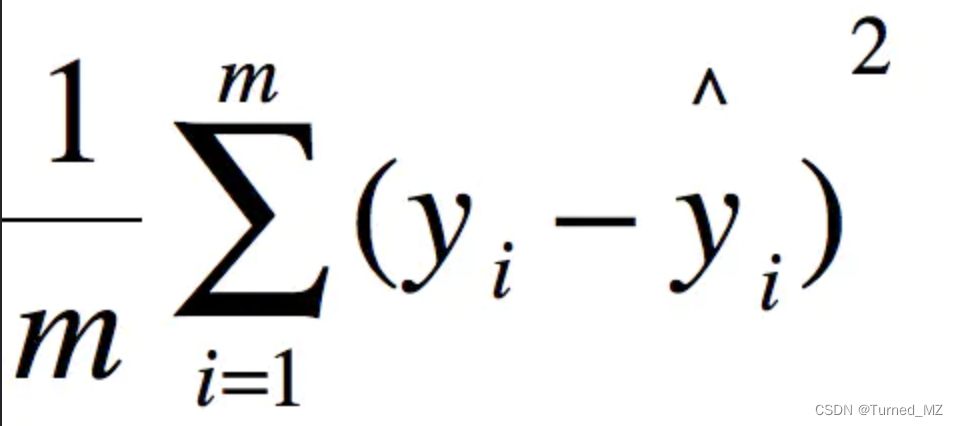&＃xff1a;&＃xff0c;yi是去噪后图像灰度值&＃xff0c;yi^是无噪声真实图像灰度值。

结构一致性相似因子

        PSNR从底层信噪的角度来评估图像的质量&＃xff0c;但是人眼对于质量的评估关注的层次其实更高&＃xff0c;根据人类视觉系统模型&＃xff0c;人眼观察图像有以下几个特点&＃xff1a;

1. 低通滤波特性&＃xff0c;即人眼对于过高的频率难以分辨。
2. 人眼对于亮度的敏感大于对颜色的敏感。
3. 对亮度的响应不是线性变换的&＃xff0c;在平均亮度大的区域&＃xff0c;人眼对灰度误差不敏感。
4. 人眼对边缘和纹理敏感&＃xff0c;有很强的局部观察能力。

        结构相似性因子是一种来源于结构相似性理论&＃xff0c;建立在人眼的视觉特征基础上的衡量两张图像相似度的指标&＃xff0c;其值越大越好&＃xff0c;最大值为1&＃xff0c;广泛用于图像质量评估领域。

        结构相似性理论认为自然图像信号是高度结构化的&＃xff0c;空域像素间有很强的相关性并蕴含着物体结构的重要信息。它没有试图通过累加与心理物理学简单认知模式有关的误差来估计图像质量&＃xff0c;而是直接估计两个复杂结构信号的结构改变&＃xff0c;并将失真建模为亮度、对比度和结构三个不同因素的组合。用均值作为亮度的估计&＃xff0c;标准差作为对比度的估计&＃xff0c;协方差作为结构相似程度的度量。

        SSIM具体的计算如下&＃xff1a;首先结构信息不应该受到照明的影响&＃xff0c;因此在计算结构信息时需要去掉亮度信息&＃xff0c;即需要减掉图像的均值&＃xff1b;其次结构信息不应该受到图像对比度的影响&＃xff0c;因此计算结构信息时需要归一化图像的方差。通常使用的计算方法如下&＃xff0c;其中C1&＃xff0c;C2&＃xff0c;C3用来增加计算结果的稳定性&＃xff0c;光度L&＃xff0c;对比度C&＃xff0c;结构对比度S计算如下&＃xff1a;

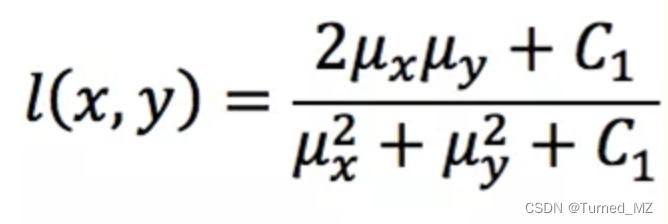
ux&＃xff0c;uy为图像的均值

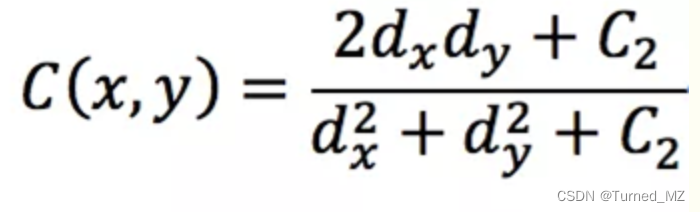
dx&＃xff0c;dy为图像的方差

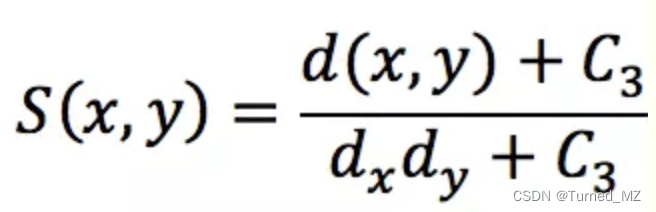
d(x,y)为图像x&＃xff0c;y的协方差。而图像质量SSIM &＃61; L(x,y)^aC(x,y)^bS(x,y)^c&＃xff0c;其中a&＃xff0c;b&＃xff0c;c分别用来控制三个要素的重要性&＃xff0c;为了计算方便可以均选择为1&＃xff0c;C1&＃xff0c;C2&＃xff0c;C3为比较小的数值&＃xff0c;通常C1&＃61;(K1×L)^2, C2&＃61;(K2×L)^2&＃xff0c;C3 &＃61; C2/2&＃xff0c; K1 <<1&＃xff0c; K2 <<1&＃xff0c;L为像素的最大值(通常为255)。当a&＃xff0c;b&＃xff0c;c都等于1&＃xff0c;C3&＃61;C2/2时&＃xff0c;SSIM的定义式就为&＃xff1a;

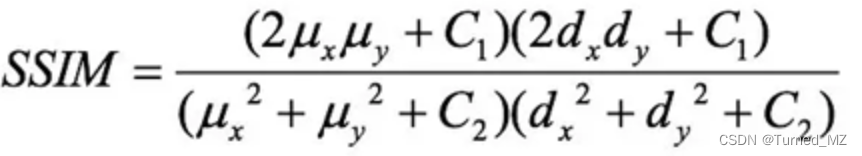
SSIM发展出了许多的改进版本&＃xff0c;其中较好的包括Fast SSIM&＃xff0c;Multi-scale SSIM。

传统去噪方法

        根据噪声引入方式的不同&＃xff0c;噪声可分为加性噪声和乘性噪声。加性噪声的幅度和信号的幅度无关&＃xff0c;是叠加到图像信号上的&＃xff0c;去除相对容易。而乘性噪声取决于信号的幅度&＃xff0c;与信号的幅度成正比&＃xff0c;去除相对困难&＃xff0c;但是如果将其取对数&＃xff0c;则乘性噪声也可以认为是加性噪声&＃xff0c;因此可以假设噪声均为加性噪声。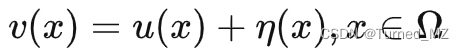&＃xff0c;其中&＃xff0c; u(x) 是原来没有噪声的图像。 x 是像素集合&＃xff0c; η(x) 是加性噪声性&＃xff0c;代表噪声带来的影响。 Ω 是像素的集合即整幅图像。

        根据噪声的性质不同&＃xff0c;噪声可分为脉冲噪声&＃xff0c;椒盐噪声&＃xff0c;高斯白噪声&＃xff0c;莱斯噪声等。在大多数去噪的研究中&＃xff0c;通常都将噪声当做高斯噪声进行处理。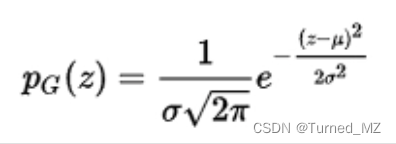

        传统的去噪方法根据去噪的原理不同可分为基于空域像素特征的方法&＃xff0c;基于频域变换的方法和基于特定模型的方法。

基于空域像素特征的方法

        基于空域像素特征的方法是通过分析在一定大小的窗口内中心像素与其他相邻像素之间早灰度空间的直接联系&＃xff0c;来获取新的中心像素的方法。

均值滤波与高斯滤波

        均值滤波与高斯滤波的不同之处在于&＃xff1a;均值滤波中&＃xff0c;滤波器中每个像素的权重是相同的&＃xff0c;即滤波器是线性的。而高斯滤波器中像素的权重与其距中心像素的距离成比例。

        算术均值滤波用像素邻域的平均灰度来代替像素值&＃xff0c;适用于脉冲噪声&＃xff0c;因为脉冲噪声的灰度级一般与周围像素的灰度级不相关&＃xff0c;而且亮度高出其他像素许多。从频率域观点来看均值滤波是一种低通滤波器&＃xff0c;高频信号将会去掉&＃xff0c;因此可以帮助消除图像尖锐噪声&＃xff0c;实现图像平滑&＃xff0c;模糊等功能。

• 方法&＃xff1a; 连续取N个采样值进行算术平均运算 。 L值较大时&＃xff1a;信号平滑度较高&＃xff0c;但灵敏度较低。L值较小时&＃xff1a;信号平滑度较低&＃xff0c;但灵敏度较高。均值滤波结果A’(i,j)随着L&＃xff08;滤波半径&＃xff09;取值的增大而变得越来越模糊&＃xff0c;图像对比度越来越小。
• 优点&＃xff1a; 适用于对一般具有随机干扰的信号进行滤波 这样信号的特点是有一个平均值&＃xff0c;信号在某一数值范围附近上下波动。
• 缺点&＃xff1a; 对于测量速度较慢或要求数据计算速度较快的实时控制不适用&＃xff0c; 比较浪费RAM。
  

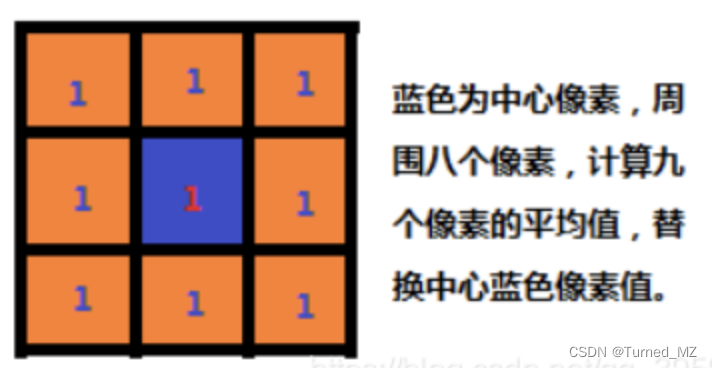
        高斯滤波矩阵的权值&＃xff0c;随着与中心像素点的距离增加&＃xff0c;而呈现高斯衰减的变换特性。这样的好处在于&＃xff0c;离算子中心很远的像素点的作用很小&＃xff0c;从而能在一定程度上保持图像的边缘特征。通过调节高斯平滑参数&＃xff0c;可以在图像特征过分模糊和欠平滑之间取得折中。与均值滤波一样&＃xff0c;高斯平滑滤波的尺度因子越大&＃xff0c;结果越平滑&＃xff0c;但由于其权重考虑了与中心像素的距离&＃xff0c;因此是更优的对邻域像素进行加权的滤波算法。

中值滤波

        中值滤波器是一种常用的非线性滤波器&＃xff0c;其基本原理是&＃xff1a;选择待处理像素的一个邻域中各像素值的中值来代替待处理的像素。主要功能使某像素的灰度值与周围领域内的像素比较接近&＃xff0c;从而消除一些孤立的噪声点&＃xff0c;所以中值滤波器能够很好的消除椒盐噪声。不仅如此&＃xff0c;中值滤波器在消除噪声的同时&＃xff0c;还能有效的保护图像的边界信息&＃xff0c;不会对图像造成很大的模糊&＃xff08;相比于均值滤波器&＃xff09;。

        中值滤波器的效果受滤波窗口尺寸的影响较大&＃xff0c;在消除噪声和保护图像的细节存在着矛盾&＃xff1a;滤波窗口较小&＃xff0c;则能很好的保护图像中的某些细节&＃xff0c;但对噪声的过滤效果就不是很好&＃xff0c;因为实际中的噪声不可能只占一个像素位置&＃xff1b;反之&＃xff0c;窗口尺寸较大有较好的噪声过滤效果&＃xff0c;但是会对图像造成一定的模糊。另外&＃xff0c;根据中值滤波器原理&＃xff0c;如果在滤波窗口内的噪声点的个数大于整个窗口内非噪声像素的个数&＃xff0c;则中值滤波就不能很好的过滤掉噪声。

双边滤波

        双边滤波是一种非线性的滤波方法&＃xff0c;是结合图像的空间邻近度和像素值相似度的一种折中处理&＃xff0c;同时考虑空间与信息和灰度相似性&＃xff0c;达到保边去噪的目的&＃xff0c;具有简单、非迭代、局部处理的特点。之所以能够达到保边去噪的滤波效果是因为滤波器由两个函数构成&＃xff1a;一个函数是由几何空间距离决定滤波器系数&＃xff0c;另一个是由像素差值决定滤波器系数。
双边滤波器中&＃xff0c;输出像素的值依赖于邻域像素的值的加权组合&＃xff0c;其公式如下&＃xff1a;

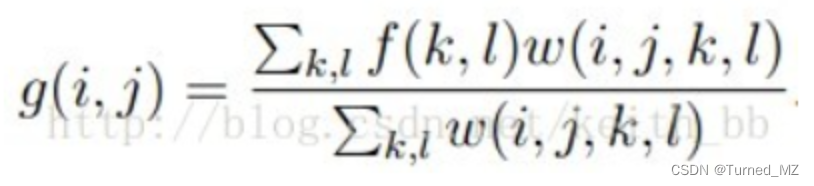
权重系数w(i,j,k,l)取决于定义域核和值域核的乘积&＃xff1a;

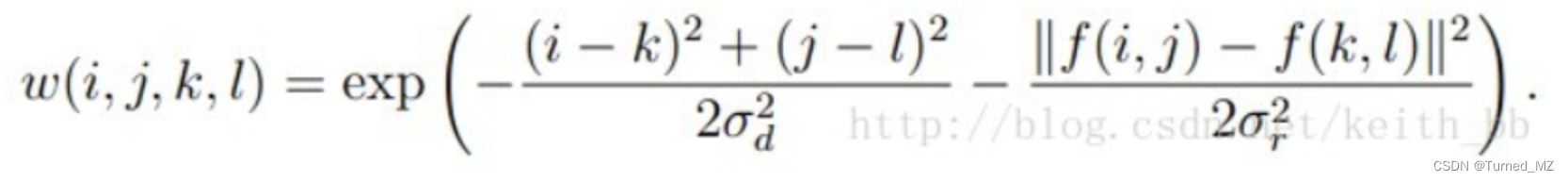
        通俗来讲就是双边滤波模板主要有两个模板生成&＃xff0c;第一个是高斯模板&＃xff0c;第二个是以灰度级的差值作为函数系数生成的模板&＃xff0c;然后这两个模板点乘就得到了最终的双边滤波模板。空域滤波器对空间上邻近的点进行加权平均&＃xff0c;加权系数随着距离的增加而减少。值域滤波器则是对像素值相近的点进行加权平均&＃xff0c;加权系数随着值差的增大而减少。
        双边滤波器可以很好的保存图像边缘细节而滤除掉低频分量的噪音&＃xff0c;但是双边滤波器的效率不是太高&＃xff0c;花费的时间相较于其他滤波器而言也比较长。

引导滤波

        引导滤波是一种复杂度为O(N)的滤波算法&＃xff0c;去噪性能非常优良&＃xff0c;已经被广泛应用于图像去噪、高对比度图像压缩、图像融合以及图像去噪等领域。引导滤波是在引导图像的作用下指导滤波的算法&＃xff0c;引导图像可以是图像本身或者是另外的图像。其原理可以参考下图&＃xff1a;引导滤波(guided filter)理解和代码实现_一只菜鸟的学习日常博的博客-CSDN博客

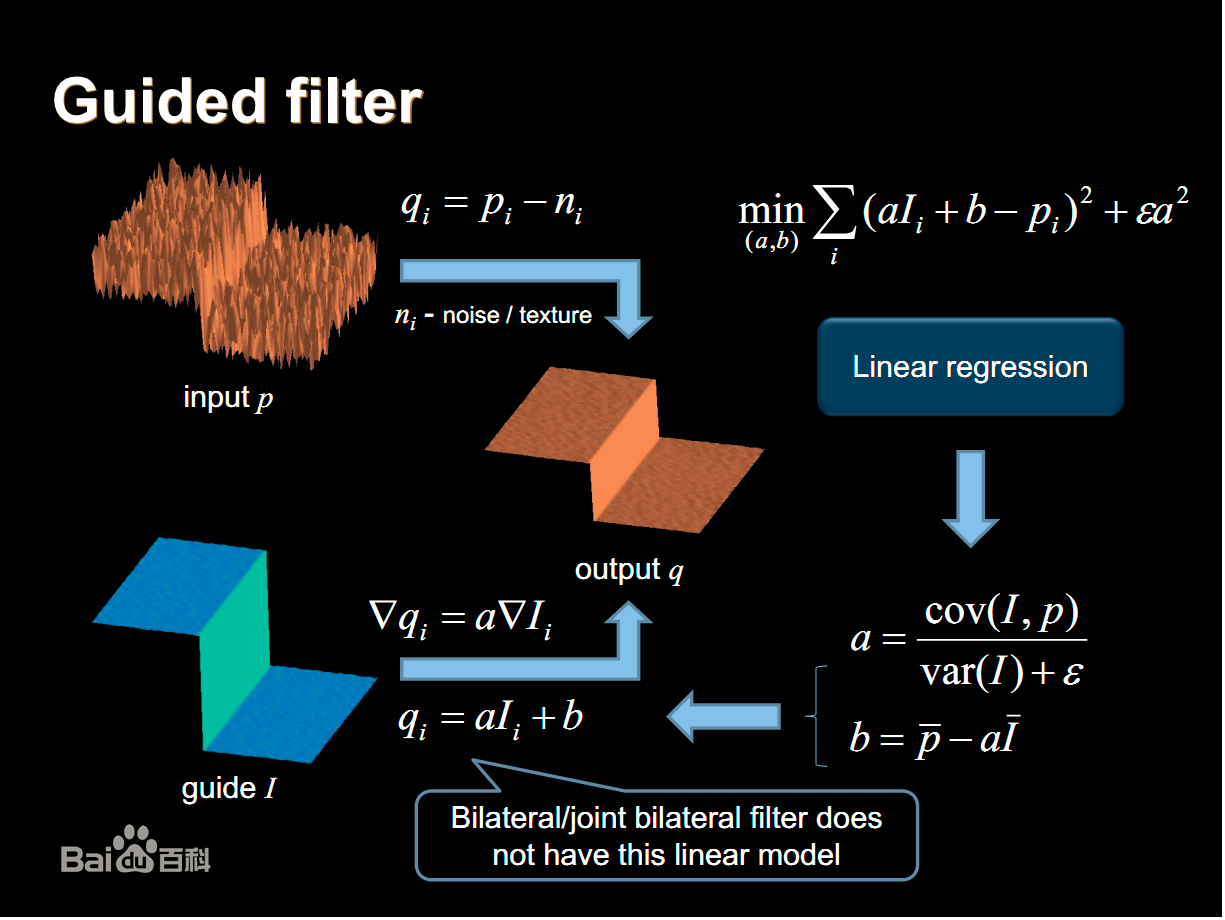
        引导滤波不像高斯滤波等线性滤波算法所用的核函数相对于待处理的图像是独立无关的&＃xff0c;而是在滤波过程中加入了引导图像&＃xff08;去噪时用的是图像本身&＃xff09;的信息&＃xff0c;所以引导滤波本质上就是通过一张引导图像I&＃xff0c;对初始图像P&＃xff08;输入图像&＃xff09;进行滤波处理&＃xff0c;使得最后的输出图像大体上与初始图像P相似&＃xff0c;但是纹理部分与引导图像I相似&＃xff0c;在滤波效果上&＃xff0c;引导滤波和双边滤波差不多&＃xff0c;在一些细节上&＃xff0c;引导滤波更好。

非局部均值滤波

        非局部均值&＃xff08;NL-means&＃xff09;滤波算法的原理与实现。其核心思路与高斯滤波很相似&＃xff1a;计算矩形窗口内所有像素点的像素值加权和&＃xff0c;权重服从高斯分布。区别在于&＃xff1a;高斯滤波使用当前滤波点与矩形窗口内其它点的空间欧式距离来计算权重&＃xff0c;距离越近权重越大&＃xff1b;而非局部均值滤波则使用当前滤波点的邻域块与矩形窗口内其它点的邻域块的相似度来计算权重&＃xff0c;相似度越大则权重越大。

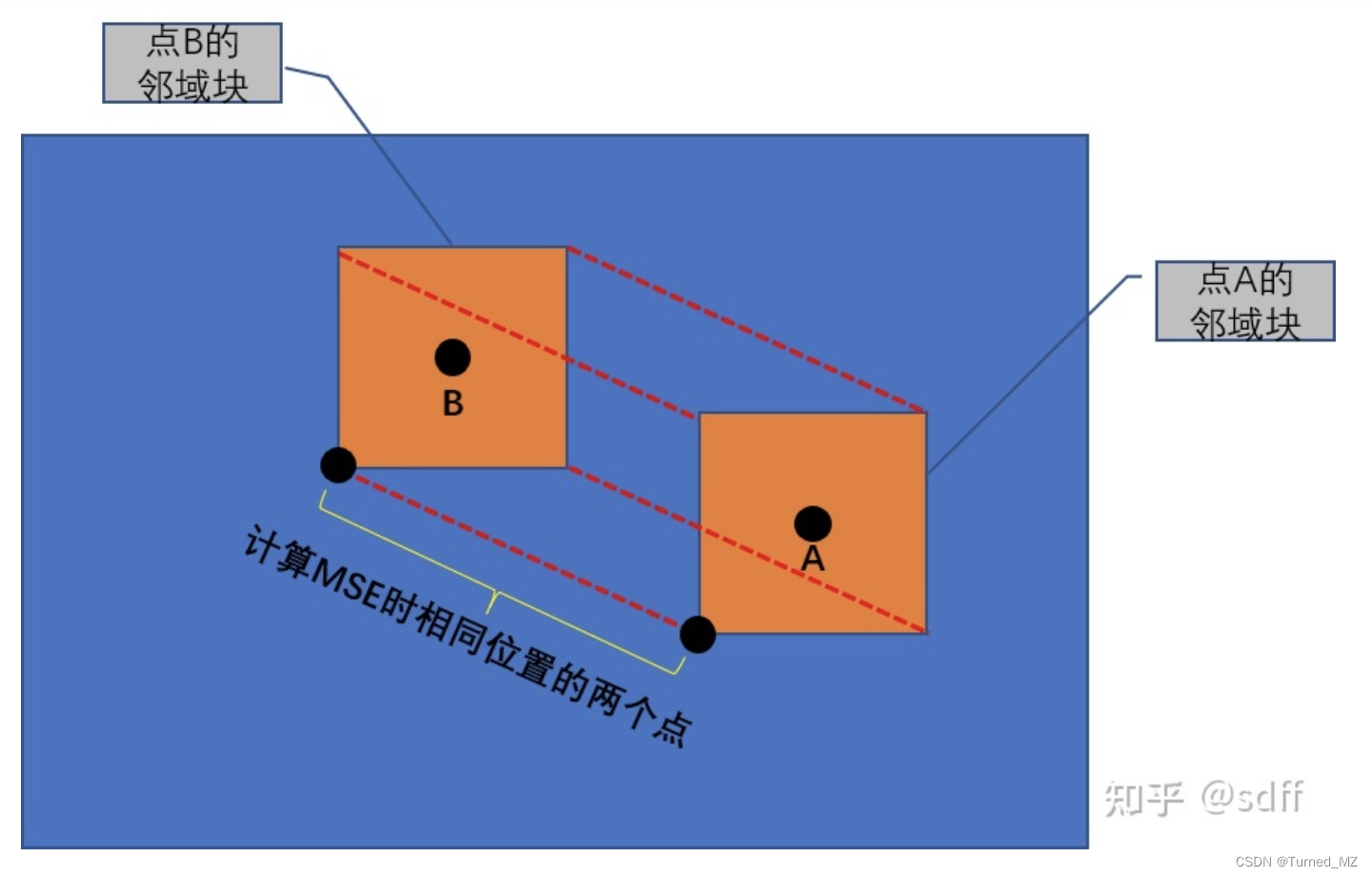
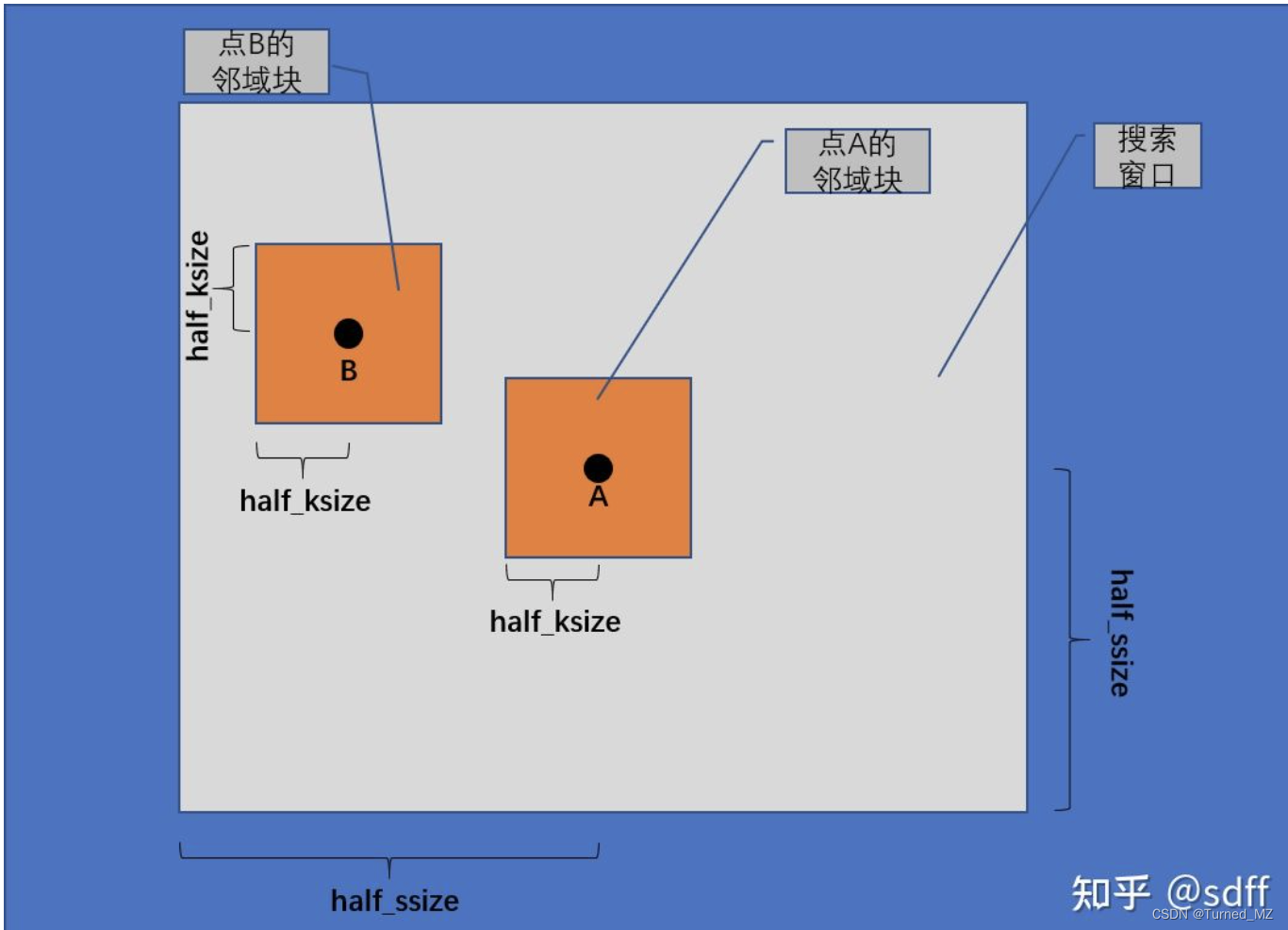
        假设点A为当前待滤波点&＃xff0c;邻域块分别取以点A和点B为中心的ksize*ksize区域&＃xff0c;矩形窗口&＃xff08;也称为搜索窗口&＃xff09;取以点A为中心ssize*ssize大小。由于ksize和ssize都是奇数&＃xff0c;通常传入它们的半值&＃xff1a;half_ksize和half_ssize。所以&＃xff0c;邻域块的大小为(2*half_ksize&＃43;1)*(2*half_ksize&＃43;1)&＃xff0c;搜索窗口的大小为(2*half_ssize&＃43;1)*(2*half_ssize&＃43;1)。如下图所示&＃xff1a;

点A的滤波值由搜索窗口内所有点的像素值加权平均得到&＃xff1a;

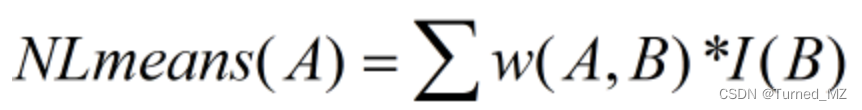
        原始的NLM算法利用图像中所有的像素来估计一个像素的值&＃xff0c;其计算量非常大&＃xff0c;因此研究者们不断对该算法做出了以下几点改进&＃xff1a;

1. 采用一定的搜索窗口来代替所有像素&＃xff1b;
2. 使用相似度阈值&＃xff0c;对于相似度低于某一阈值的像素&＃xff0c;不加入权重的计算&＃xff1b;
3. 使用块之间的显著特征&＃xff0c;如纹理特征等代替灰度值的欧氏距离来计算相似度&＃xff0c;在计算上更加灵活。

        NLM滤波算法对于边缘的保持能力最差。

 基于频域的去噪方法

        图像变换域去噪算法的基本思想其实就是首先进行某种变换&＃xff0c;将图像从空间域转换到变换域&＃xff0c;然后从频率上把噪声分为高中低频噪声&＃xff0c;用这种变换域的方法就可以把不同频率的噪声分离&＃xff0c;之后进行反变换将图像从变换域转换到原始空间域&＃xff0c;最终达到去除图像噪声的目的。

        傅立叶变换用于分析各种滤波器的频率特性&＃xff0c;对于一幅图像来说在分析其频率特性时&＃xff0c;它的边缘&＃xff0c;突出部分以及颗粒噪声往往代表图像信号的高频分量&＃xff0c;而大面积的图像背景区则代表图像信号的低频分量。因此&＃xff0c;使用滤波的方法滤除其高频部分也就可以去除噪声&＃xff0c;使得图像得到一定的平滑。具体原理可以参考下面的文章&＃xff0c;这里不再细讲了&＃xff1a;传统的图像去噪方法&＃xff08;四&＃xff09;之变换域去噪算法_打着灯笼摸黑的博客-CSDN博客_变换域算法

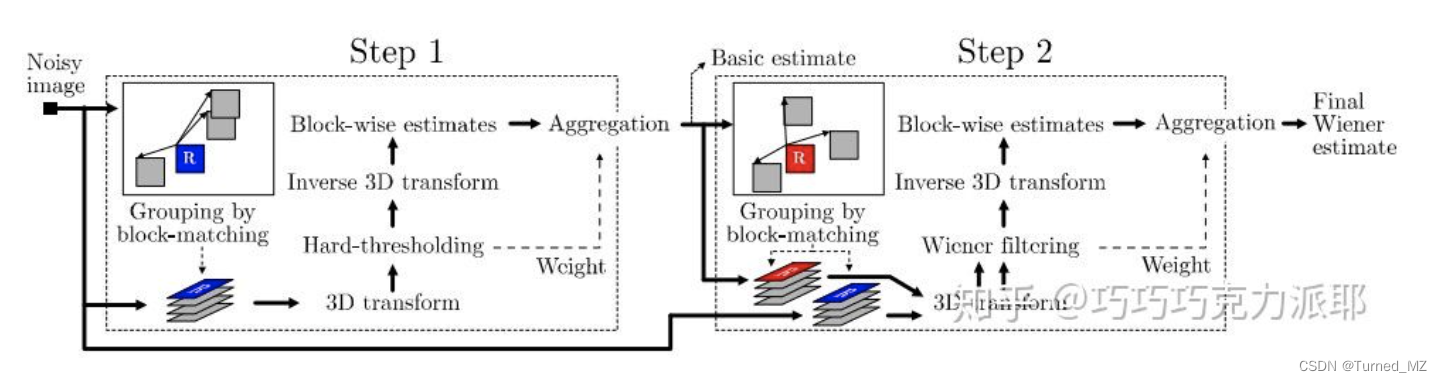
BM3D算法

        有两种噪声算法&＃xff0c;一种是非局部去噪方法Non-local method&＃xff0c;是一种空间算法&＃xff0c;另一种transform method是一种转换算法&＃xff0c;都在图像去噪中得到很好的效果&＃xff0c;所以自然而然地想&＃xff1a;同时使用两种算法效果如何&＃xff1f;这便引出了BM3D去噪算法。

        BM3D&＃xff08;Block-matching and 3D filtering&＃xff0c;3维块匹配滤波&＃xff09;是当前效果最好的算法之一。该算法通过相似判定找到与参考块相近的二维图像块&＃xff0c;并将相似块按照组合成三维群组&＃xff0c;对三维群组进行协同滤波处理&＃xff0c;再将处理结果聚合到原图像块的位置。该算法的思想跟NL-Means有点类似&＃xff0c;也是在图像中寻找相似块的方法进行滤波&＃xff0c;但是相对于NL-Means要复杂许多。

        算法总体流程图如下&＃xff0c;其原理可以参考&＃xff1a;BM3D算法学习 - 知乎

 
参考文档&＃xff1a;
传统图像去噪方法&＃xff08;一&＃xff09;_打着灯笼摸黑的博客-CSDN博客_传统去噪方法

图像滤波常用算法实现及原理解析_小白学视觉的博客-CSDN博客

引导滤波(guided filter)理解和代码实现_一只菜鸟的学习日常博的博客-CSDN博客

非局部均值滤波&＃xff08;NL-means&＃xff09;算法的原理与C&＃43;&＃43;实现 - 知乎

传统的图像去噪方法&＃xff08;四&＃xff09;之变换域去噪算法_打着灯笼摸黑的博客-CSDN博客_变换域算法

BM3D算法学习 - 知乎

书籍&＃xff1a;《深度学习之摄影图像处理》