辐照度(irradiance)定义为电磁辐射入射于曲面时每单位面积的功率&＃xff0c;直观理解为能量在入射点处的量化值。在计算机图形学中&＃xff0c;就是要求解场景中任意位置的辐照度大小。如果求得辐照度的大小&＃xff0c;剩下的事情就是如何利用所求解得到的辐照度渲染出一张静帧图像&＃xff0c;而不同的求解方法&＃xff0c;对应着不同的渲染算法&＃xff0c;每一个算法都有其独特的风格。本部分就是要理清计算机图形学中最基本的辐照度物理量之间的定义与关系。
1.1 立体角
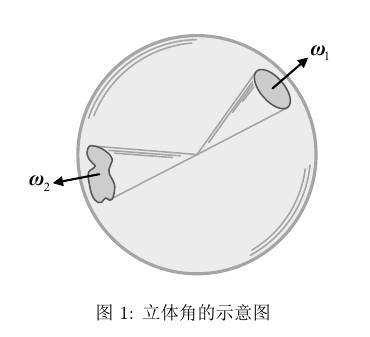
立体角的概念其实是平面几何中角的概念的扩展。数学上定义平面角度是在单位圆上&＃xff0c;两射线张角的弧长即为张出的角度&＃xff0c;单位为radian&＃xff1b;则类比平面几何中对角度的定义&＃xff0c;我们可以去如下定义立体角的概念&＃xff1a;在单位球体上&＃xff0c;球心处一个锥形包含的球表面积定义为这个锥形的立体角(如图1)&＃xff0c;单位为stereo radian&＃xff0c;简写为sr。计算机图形学中常用粗体的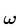
来表示一个立体角。需要注意的是&＃xff0c;立体角的形状并不仅限于像图1中
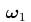那样的锥形&＃xff0c;还可以是像
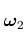那样的不规则形状&＃xff0c;我们仅用单位圆内该立体角内部包含的球表面积来度量它的角度&＃xff0c;由于单位球面的表面积为$4\pi$&＃xff0c;所以一个立体角的取值范围也在$\left[{0,4\pi}\right]$之间。有了上述的介绍&＃xff0c;我们就可以继续定义立体角的微分了。即当一个立体角所包含的单位球表面积趋于$0$时&＃xff0c;我们称其为立体角的微分&＃xff0c;写为
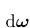。为表述简便&＃xff0c;后续有关“方向”的概念&＃xff0c;如果没有特殊说明&＃xff0c;默认都是在说指向这个方向的一个立体角。
1.2 辐照度中的基本量及其关系
辐照度学中&＃xff0c;定义了如下表1的常见基本量&＃xff0c;详细请参见相关的教材。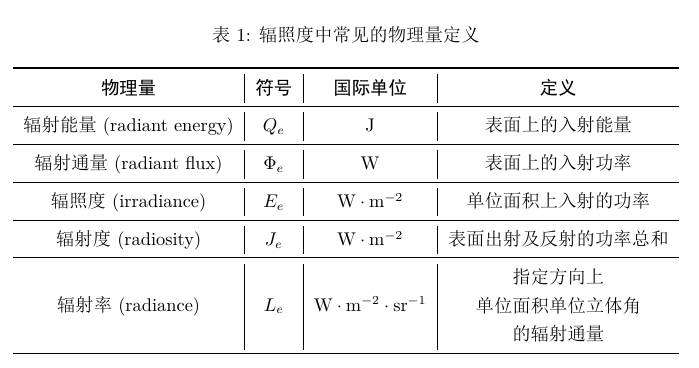
上述物理量中&＃xff0c;较为常用的几个物理量为辐射通量$\Phi_e$、辐照度$E_e$和辐射率$L_e$。为表述简便&＃xff0c;后续的内容都会省略角标&＃xff0c;即简写为$\Phi$、$E$和$L$。现定义它们之间满足的基本关系。
\begin{equation}
\label{eq:E}
{E}&＃61;\frac{{{\rm{d}}{\Phi}}}{{{\rm{d}}A}}
\end{equation}
式中之所以用单位面积$\rm{d}A$上入射的功率$\Phi$而不是能量$Q$来定义辐照度$E$是因为前者考虑了时间因素&＃xff0c;把时间度量统一到单位时间。如果按照后者来定义的话&＃xff0c;会造成物理量$E$与时间相关&＃xff0c;这样做并不是一个明智的选择。
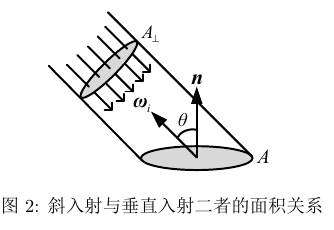
定义垂直入射光方向的辐照度
\begin{equation}
\label{eq:Ebot}
{E_\bot}&＃61;\frac{{{\rm{d}}{\Phi}}}{{{\rm{d}}A_\bot}}
\end{equation}
根据图2&＃xff0c;上式中的$A_\bot$与$A$有如下的关系
\begin{equation}
\label{eq:aabot}
{A_\bot}&＃61;A\cos\theta
\end{equation}
式(\ref{eq:aabot})中&＃xff0c;$\theta$是入射方向与法线的夹角&＃xff0c;注意这里的$\theta$取值范围为$0\le\theta\le\frac{\pi}{2}$&＃xff0c;使得$cos\theta$总是非负数。为简便起见&＃xff0c;我们规定入射方向是沿着入射点朝向入射源的&＃xff0c;直观上这与“入射”的含义相悖&＃xff0c;但是并不影响后续的分析。这样一来&＃xff0c;所有有关“方向”的概念都是沿物体表面入射点朝向表面外&＃xff0c;反而会使很多式子的形式得到简化。我们进而又能很简单地得到$E$与$E_\bot$之间的关系
\begin{equation}
\label{eq:eebot}
{E_\bot}&＃61;\frac{E}{\cos\theta}
\end{equation}
有了式(\ref{eq:E})&＃xff0c;我们可以进一步定义辐射率
\begin{equation}
\label{eq:L}
{L}&＃61;\frac{{{\rm{d}}{E_\bot}}}{{{\rm{d}}\bf{\omega}}}
\end{equation}
所以
\begin{equation}
\label{eq:llbot}
L&＃61;\frac{{{{\rm{d}}}\Phi }}{{{\rm{d}}{A_ \bot }{\rm{d}}\bf{\omega} }} &＃61; \frac{{{{\rm{d}}}\Phi }} {{\rm{d}}A{\rm{d}}\bf{\omega}\cos\theta}
\end{equation}
由(\ref{eq:eebot})、(\ref{eq:L})可得
\begin{equation}
\label{eq:elrelation}
{\rm{d}} E &＃61; L\cos \theta {\rm{d}}{\bf{\omega}}
\end{equation}
之所以定义辐射率的概念&＃xff0c;是因为我们经常要衡量单位球表面上任意一点的辐照度&＃xff0c;但是点的面积是不存在的&＃xff0c;所以要用辐照度微分与立体角微分之比的形式来定义辐射率。式(\ref{eq:llbot})、(\ref{eq:elrelation})是很重要的公式&＃xff0c;在之后对表面处的辐射率估计的推导中会经常用到。
1.3 符号约定
由于后续的推导过程中运用了大量的数学概念&＃xff0c;我们在正式介绍这些内容之前&＃xff0c;首先要约定符号的写法以及各种物理量的表达方式&＃xff0c;否则很容易造成混淆。我们规定&＃xff1a;
1) 立体角用粗体小写的$\bf{\omega}$来表示&＃xff0c;其微分形式为${\rm{d}}{\bf{\omega}}$&＃xff0c;这在1.1节中已经陈述。
2) 以物体表面任意点$x$处&＃xff0c;沿表面局部法线建立的半球面区域写为$\Omega_x$&＃xff0c;其立体角恒为$2\pi$。
3) 双向反射分布函数(下文会详细介绍)用$f_r$来表示&＃xff0c;且其第一个参数$x$为参考点的位置&＃xff0c;第二个参数为入射方向&＃xff0c;第三个参数为出射方向。
4) 表1中的辐照度(irradiance)和辐射度(radiosity)的符号应该予以统一&＃xff0c;以符号$E_i$表示辐照度&＃xff0c;以符号$E_o$表示辐射度。类似地&＃xff0c;规定入射辐射率符号为$L_i$&＃xff0c;出射辐射率符号为$L_o$。
1.4 双向反射分布函数(BRDF)
1.4.1 BRDF的定义
双向反射分布函数(Bidirectional Reflectance Distribution Function, BRDF)&＃xff0c;是用于描述物体表面性质的重要函数之一&＃xff0c;它被定义为沿出射光方向$\bf{\omega}_o$出射的辐射率$L_o$与沿入射光方向$\bf{\omega}_i$入射的辐照度$E_i$的比值&＃xff0c;单位为$\rm{sr^{-1}}$。由上述表述&＃xff0c;则在物体表面$x$点处的BRDF的定义式即为
\begin{equation}
\label{eq:brdfdef}
f_r \left( {x,\bf{\omega} _i ,\bf{\omega} _o } \right) &＃61; \frac{{{\rm{d}}L_o (x,\bf{\omega} _o )}}{{{\rm{d}}E_i (x,\bf{\omega} _i )}} &＃61; \frac{{{\rm{d}}L_o \left( {x,\bf{\omega} _o } \right)}}{{{\rm{d}}E_{i,\bot} \left( {x,\bf{\omega} _i } \right)\cos \theta _i }} &＃61; \frac{{{\rm{d}}L_o \left( {x,\bf{\omega} _o } \right)}}{{L_i \left( {x,\bf{\omega} _i } \right)\cos \theta _i {\rm{d}}\bf{\omega} _i }}
\end{equation}
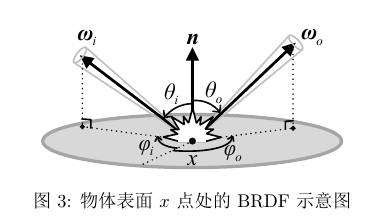
如图3所示&＃xff0c;为形式简便&＃xff0c;将入射方向规定为由参考点指向源点&＃xff0c;这样所有有关方向的物理量均统一为沿表面指向外界。${\bf{n}}$为物体局部法线&＃xff0c;一束入射方向为$\bf{\omega}_i$的光线击中物体表面$x$点处&＃xff0c;其能量会在以$x$点处形成的半球面沿一定分布特征辐射出去。那么以$\bf{\omega}_i$为入射方向&＃xff0c;以$\bf{\omega}_o$为我们要考察的出射方向&＃xff0c;沿$\bf{\omega}_o$方向出射的能量${\rm{d}}{L_o}$与入射光线在$x$点处对物体表面的辐照度贡献${\rm{d}}{E_i}$之比&＃xff0c;即被定义为在$x$处&＃xff0c;沿入射方向$\bf{\omega}_i$和出射方向$\bf{\omega}_o$的双向反射系数$f_r\left({x,\bf{\omega}_i,\bf{\omega}_o}\right)$。
这里请注意式(\ref{eq:brdfdef})中“$\rm{d}$”的含义与数学上严格意义上的微分是有区别的&＃xff0c;$L_o\left(x,{\bf{\omega}}_o\right)$是指在物体表面$x$点处&＃xff0c;半球面${\bf{\omega}}_x$区域内所有入射光的能量总和作为输入时&＃xff0c;沿${\bf{\omega}}_o$方向出射的辐射率&＃xff1b;而${\rm{d}}L_o\left(x,{\bf{\omega}}_o\right)$则特指以方向${\bf{\omega}}_i$处入射光的能量作为输入时&＃xff0c;沿${\bf{\omega}}_o$方向出射的辐射率。${\rm{d}}E_i\left(x,{\bf{\omega}}_i\right)$特指方向${\bf{\omega}}_i$处的辐照度。${\rm{d}}E_i\left(x,{\bf{\omega}}_i\right)$和$E_i\left(x,{\bf{\omega}}_i\right)$的含义是相同的。
针对BRDF的定义式&＃xff0c;有如下两个问题需要解释&＃xff1a;
1) 为什么要用微分形式去定义&＃xff1f;
2) 为什么不定义成$\frac{{\rm{d}}{L_o}}{{\rm{d}}{L_i}}$或者$\frac{{\rm{d}}{E_o}}{{\rm{d}}{E_i}}$&＃xff0c;使得它变成一个纯粹的系数而不是一个具有量纲$\rm{sr^{-1}}$这样奇怪的一个物理量&＃xff1f;
接下来我们就来回答上面两个问题。之所以要用微分形式去定义&＃xff0c;在于后面有关BRDF的所有计算几乎都涉及到积分&＃xff0c;所以原始的BRDF定义式将BRDF定义为微分形式会更有利于后续对积分式的计算&＃xff0c;而且形式美观简洁&＃xff0c;但之后进行公式推导时&＃xff0c;仍需要明确分子的$L_o$是特指${\bf{\omega}}_i$方向上对出射辐射率的贡献&＃xff0c;以后为强调这个事实&＃xff0c;也常用$L_o \left( {x,{\bf{\omega}} _o } \right)\left| {_{{\bf{\omega}} _i } } \right.$表示${\rm{d}}L_o\left(x,{\bf{\omega}}_o\right)$&＃xff1b;而针对BRDF的量纲问题&＃xff0c;则可以这样解释&＃xff1a;BRDF的定义是根据对实际现象的物理建模而得出的&＃xff0c;这个量也最好应该能够通过实验仪器测得&＃xff0c;那么定义式的形式&＃xff0c;实际上就决定了对测量仪器的要求。直接测量物体表面某点沿某入射方向的入射光辐照率$L_i$是有困难的&＃xff0c;而想测量沿着某一方向的出射辐射率$L_o$则很简单&＃xff0c;只需要将一个管状测量仪器对准入射点处&＃xff0c;就能测得沿着管状测量仪出射的辐射率$L_o$。虽然测量入射光辐照率由困难&＃xff0c;但是测量入射光的辐照度$E_i$则很简单&＃xff0c;因为辐照度没有方向的概念&＃xff0c;所以研究者仅需要制作一个半球状的光线接收器即可。
实际计算的时候&＃xff0c;通常是以物体表面参考点$x$为原点&＃xff0c;以物体表面$x$点处指向物体表面外侧的局部法线${\bf{n}}$为$z$轴建立的求坐标系来进行积分的求解&＃xff0c;所以式(\ref{eq:brdfdef})中的BRDF定义式也可以写为$f_r \left( {x,\theta _i ,\varphi _i ,\theta _o ,\varphi _o } \right)$&＃xff0c;如果物体表面的反射特性与参考点$x$的位置无关(通常情况下)&＃xff0c;那么我们可以在$f_r$中省略变量$x$&＃xff0c;变为$f_r \left( {\theta _i ,\varphi _i ,\theta _o ,\varphi _o } \right)$&＃xff0c;图3中$\theta _i$、$\varphi _i$是${\bf{\omega}}_i$的球坐标系参数表示&＃xff0c;$\theta _o$、$\varphi _o$是${\bf{\omega}}_o$的球坐标系参数表示。
很多实验室测得的BRDF数据都是一个巨大的四维表格(例如MERL BRDF数据库&＃xff0c;每种材质表面测得的BRDF数据有34MB&＃xff0c;具体详见http://www.merl.com/brdf/)&＃xff0c;用户在实际使用这张表格的时候&＃xff0c;就是依据$\theta _i$、$\varphi _i$、$\theta _o$和$\varphi _o$四个独立变量来查表得到对应的BRDF值&＃xff0c;进而完成渲染的。
1.4.2 BRDF的性质
BRDF具有以下三条重要性质&＃xff1a;
1) 非负性&＃xff1a;对于物体表面上任意点$x$以及半球面内所有${\bf{\omega}}_i$和${\bf{\omega}}_o$&＃xff0c;BRDF函数值均非负。这一性质很好理解&＃xff0c;即便是绝对黑体&＃xff0c;它的BRDF也是恒为$0$而不可能出现负值。
\begin{equation}
f_r\left({x,{\bf{\omega}}_i,{\bf{\omega}}_o}\right) \ge 0
\end{equation}
2) 互易性&＃xff1a;由基本光路可逆原理&＃xff0c;若交换入射方向和出射方向&＃xff0c;BRDF函数值不变。此性质可将原始BRDF数据量降为原来的一半。
\begin{equation}
f_r\left({x,{\bf{\omega}}_i,{\bf{\omega}}_o}\right) &＃61; f_r\left({x,{\bf{\omega}}_o,{\bf{\omega}}_i}\right)
\end{equation}
3) 能量守恒性&＃xff1a;沿半球面向外辐射的辐射率总和应小于等于入射光的辐射率总和。即对于$\forall {\bf{\omega}}_i$&＃xff0c;
\begin{equation}
\int\limits_{ \Omega _x } {f_r \left( {x,{\bf{\omega}} _i ,{\bf{\omega}} _o } \right)\cos {\theta _o } {\rm{d}}{\bf{\omega}} _o } \le 1
\end{equation}
BRDF的能量守恒性可以用来鉴别给定的BRDF函数是否合理&＃xff0c;同时也可以给未归一化的BRDF进行归一化操作。下面我们就来简单证明一下上述的能量守恒性。
证明&＃xff1a;假设有一束辐照度$E_i \left( {x,{\bf{\omega}} _i } \right)$
的光线&＃xff0c;沿${\bf{\omega}}_i$方向入射并击中物体表面$x$点处。设$x$点处朝物体表面外的半球面区域为$\Omega_x$&＃xff0c;由能量守恒定律&＃xff0c;在排除该物体表面为光源的前提下&＃xff0c;沿半球面$\Omega_x$向外辐射的所有辐射度之和应小于等于入射光的辐照度。即满足
\begin{equation*}
\label{eq:energy_conservation}
\int\limits_{\Omega _x } {{\rm{d}}\left[ {E_o \left( {x,{\bf{\omega}} _o } \right)\left| {_{{\bf{\omega}} _i } } \right.} \right]} \le E_i \left( {x,{\bf{\omega}} _i } \right)
\end{equation*}
上式中的$E_o \left( {x,{\bf{\omega}} _o } \right)\left| {_{{\bf{\omega}} _i } } \right.$是特指沿方向${\bf{\omega}}_i$入射的光线所造成的辐射度贡献。
由式(\ref{eq:elrelation})可得
\begin{equation*}
\int\limits_{\Omega _x } {\left[ {L_o \left( {x,{\bf{\omega}} _o } \right)\left| {_{{\bf{\omega}} _i } } \right.} \right]{\rm{cos}}\theta _{\rm{o}} {\rm{d}}{\bf{\omega}} _o } \le E_i \left( {x,{\bf{\omega}} _i } \right)
\end{equation*}
根据式(\ref{eq:brdfdef})&＃xff0c;又有
\begin{equation*}
\int\limits_{\Omega _x } {\left[ {f_r \left( {x,{\bf{\omega}} _i ,{\bf{\omega}} _o } \right)E_i \left( {x,{\bf{\omega}} _i } \right)} \right]{\rm{cos}}\theta _o {\rm{d}}{\bf{\omega}} _o } \le E_i \left( {x,{\bf{\omega}} _i } \right)
\end{equation*}
即
$$
\int\limits_{\Omega _x } {f_r \left( {x,{\bf{\omega}} _i ,{\bf{\omega}} _o } \right)\cos \theta _o {\rm{d}}{\bf{\omega}} _o } \le 1
$$
对于$\forall {\bf{\omega}}_i$均成立。
京公网安备 11010802041100号