机器学习——KMeans算法

相似度或距离

　　假设有 $m$ 个样本，每个样本由 $n$ 个属性的特征向量组成，样本合集 可以用矩阵 $X$ 表示

　　　　$X=[x_{ij}]_{mn}=\begin{bmatrix}x_{11}&x_{12} &  ... &x_{1n} \\x_{21}&x_{22} &  ... &x_{2n} \\...& ... &  ...& ...\\x_{m1}&x_{m2} & ...&x_{mn}\end{bmatrix}$

　　聚类的核心概念是相似度(similarity)或距离(distance)，有多种相似度或距离定义。因为相似度直接影响聚类的结果，所以其选择是聚类的根本问题。

闵可夫斯基距离

　　闵可夫斯基距离越大相似度越小，距离越小相似度越大。

　　给定样本集合 $X$, $X$ 是 $m$ 维实数向量空间 $R^{n}$ 中点的集合，其中

　　　　$x_{i},x_{j}\in X,x_{i}=(x_{1i},x_{2i},...,x_{ni})^{T},x_{j}=(x_{1j},x_{2j},...,x_{nj})^{T}$

　　样本 $x_{i}$ 与样本 $x_{j}$ 的闵可夫斯基距离（Minkowski distance）定义为

　　　　$d_{ij}=(\sum \limits_{k=1}^{n}|x_{ki}-x_{kj}|^{p})^{\frac{1}{p}},p\ge 1$

　　当 $p=2$ 时称为欧氏距离(Euclidean distance) 

 　　　　$d_{ij}=(\sum \limits_{k=1}^n|x_{ki}-_{kj}|^2)^{\frac{1}{2}}$

　　当 $p=1$ 时称为曼哈顿距离(anhattan distance)

　　　　$d_{ij}=\sum \limits_{k=1}^n|x_{ki}-x_{kj}|$

　　当 $p=\infty$ 时称为切比雪夫距离(Chebyshev distance)

 　　　　$d_{ij}=\max_{k}|x_{ki}-x_{kj}|$

相关系数

　　• 样本之间的相似度也可以用相关系数(correlation coefficient)来表示。
　　• 相关系数的绝对值越接近于1，表示样本越相似，越接近于0，表示样本越不相似。
　　• 样本 $x_{i}$ 与样本 $x_{j}$ 之间的相关系数定义为

　　　　$r_{ij}=\frac{\sum_\limits {k=1}^{n}(x_{ki}-\overline{x_{i}})(x_{kj}-\overline{x_{j}}) }{[\sum \limits _{k=1}^{n} (x_{ki}-\overline{x_{i}})^{2}\sum \limits _{k=1}^{n} (x_{kj}-\overline{x_{j}})^{2}]^{\frac{1}{2} }} $    其中$\overline{x_{i}} =\frac{1}{n} \sum \limits_{k=1}^{n} x_{ki},\overline{x_{j}} =\frac{1}{n} \sum \limits_{k=1}^{n} x_{kj}$

夹角余弦

　　• 样本之间的相似度也可以用夹角余弦(cosine)来表示。
　　• 夹角余弦越接近于1，表示样本越相似
　　• 越接近于0，表示样本越不相似。
　　• 样本 $x_{i}$ 与样本 $x_{j}$之间的夹角余弦定义为

　　　　$s_{ij}=\frac{\sum_ \limits{k=1}^{n}x_{ki}x_{kj}}{[\sum_ \limits{k=1}^{n} x_{ki}^{2}\sum_ \limits{k=1}^{n} x_{kj}^{2}]^{\frac{1}{2} }} $

相似度

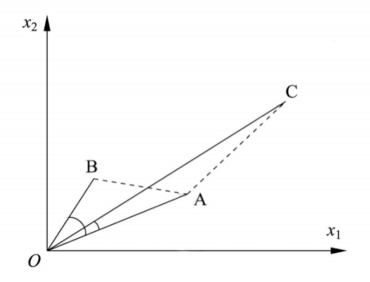
　　• 用距离度量相似度时，距离越小样本越相似；
　　• 用相关系数时，相关系数越大样本越相似；
　　• 注意不同相似度度量得到的结果并不一定一致。
　　• 从右图可以看出，如果从距离的角度看， A和B比A和C更相似，但从相关系数的角度看，A和C比A和B更相似。

类或簇

　　• 通过聚类得到的类或簇，本质是样本的子集。
　　• 如果一个聚类方法假定一个样本只能属于一个类，或类的交集为空集，那么该方法称为硬聚类(hard clustering)方法。
　　• 如果一个样本可以属于多个类，或类的交集不为空集，那么该方 法称为软聚类(soft clustering)方法。
　　• 用G表示类或簇（cluster)，用$x_{i}$, $x_{j}$表示类中的样本，用$n_{G}$表示 $G$ 中样本的个数，用$d_{ij}$表示样本$x_{i}$与样本$x_{j}$之间的距离。
　　• 类或簇有多种定义，下面给出几个常见的定义：

　　定义一：设$T$为给定的正数，若集合$G$中任意两个样本$x_{i}$, $x_{j}$，有
　　　　$d_{ij}
　　则称 $G$ 为一个类或者簇。
　　定义二：设 $T$ 为给定的正数，若集合 $G$ 中任意样本 $x_{i}$，一定存在 $G$ 中的另一个样本 $x_{j} $，使得
　　　　$d_{ij}
　　则称$G$为一个类或者簇。
　　定义三：设 $T$ 为给定的正数，若集合 $G$ 中任意样本 $x_{i}$， $G$ 中的另一个样本 $x_{j}$满足
　　　　$\frac{1}{n_{G}-1} \sum \limits _{x_{i}\in G}d_{ij}\le T$
　　其中 $n_{G}$ 为 $G$ 中样本的个数，则称 $G$ 为一个类或者簇。
　　定义四：设 $T$ 和 $V$ 为给定的正数，若集合 $G$ 中任意两个样本 $x_{i}$，$x_{i}$的距离$d_{ij}$满足
　　　　$\frac{1}{n_{G}(n_{G}-1)} \sum \limits _{x_{i}\in G} \sum \limits _{x_{j}\in G}d_{ij}\le T,d_{ij}\le V$
　　则称G为一个类或者簇。

类特征

　　(1)类中心：即类的均值
　　　　$\bar{x}_{G} =\frac{1}{n_{G}} \sum \limits _{i=1}^{n_{G}}x_{i}$
　　式中$n_{G}$是类$G$的样本个数。
　　(2)类的直径：$D_{G}$是任意类中两个样本之间的最大距离，即
　　　　$D_{G}=\underset{x_{i},x_{j}\in G}{max} d_{ij}$
　　(3)类的样本散布矩阵$A_{G}$与样本协方差矩阵$S_{G}$
　　样本散布矩阵$A_{G}$为
　　　　$A_{G}=\sum \limits _{i=1}^{n_{G}}(x_{i}-\overline{x_{G}})(x_{i}-\overline{x_{G}})^T$
　　样本协方差矩阵$S_{G}$为
　　　　$S_{G}=\frac{1}{n-1}A_{G} =\frac{1}{n-1}\sum \limits _{i=1}^{n_{G}}(x_{i}-\overline{x_{G}})(x_{i}-\overline{x_{G}})^T$

类与类之间的距离 

　　下面考虑类$G_p$与类$G_q$之间的距离$D(p,q)$，也称为连接（linkage)。类与类之间的距离也有多种定义。
　　设类$G_p$包含$n_p$个样本，$G_q$包含$n_q$个样本，分别用$\bar{x}_{p}$和$\bar{x}_{q}$表示$G_p$和$G_q$的均值，即类的中心 。
　　最短距离或单连接(single linkage)
　　定义类$G_p$的样本与$G_q$的样本之间的最短距离为两类之间的距离
　　　　$D_{pq}=min\{ d_{ij}|x_{i} \in G_{p},x_{j} \in G_{q}\}$

　　最长距离或完全连接(complete linkage)
　　定义类$G_p$的样本与$G_q$的样本之间的最长距离为两类之间的距离
　　　　$D_{pq}=max\{ d_{ij}|x_{i} \in G_{p},x_{j} \in G_{q}\}$

　　中心距离
　　定义类$G_p$与$G_q$的中心$\bar{x}_{p}$ 与$\bar{x}_{q}$之间的距离为两类之间的距离
　　　　$D_{pq}=d_{\bar{x}_{p}\bar{x}_{q}}$

　　平均距离
　　定义类$G_p$与$G_q$任意两个样本之间距离的平均值为两类之间的距离
　　　　$D_{pq}=\frac{1}{n_{p}n_{q}}\sum \limits _{x_{i} \in G_{p}}\sum \limits _{x_{j} \in G_{q}}d_{ij}$

 2 K-Means算法

　　$K-Means$算法是无监督的聚类算法，实现简单，聚类效果也不错，因此应用很广泛。$K-Means$算法有大量的变体，本文就从最传统的$K-Means$算法讲起，在其基础上讲述$K-Means的$优化变体方法。包括初始化优化$K-Means++$, 距离计算优化$elkan K-Means$算法和大数据情况下的优化$Mini Batch K-Means$算法。

2.1 K-Means原理初探

　　$K-Means$算法的思想很简单，对于给定样本集，按照样本之间距离大小，将样本集划分为$K$个簇。让簇内的点尽量紧密相连，让簇间距离尽量大。

　　如果用数据表达式表示，假设簇划分为$(C_1,C_2,...C_k)$，则我们的目标是最小化平方误差E：　　　　

　　　　$E = \sum\limits_{i=1}^k\sum\limits_{x \in C_i} ||x-\mu_i||_2^2$

　　其中$\mu_i$是簇$C_i$的均值向量，有时也称为质心，表达式为：

　　　　$\mu_i = \frac{1}{|C_i|}\sum\limits_{x \in C_i}x$

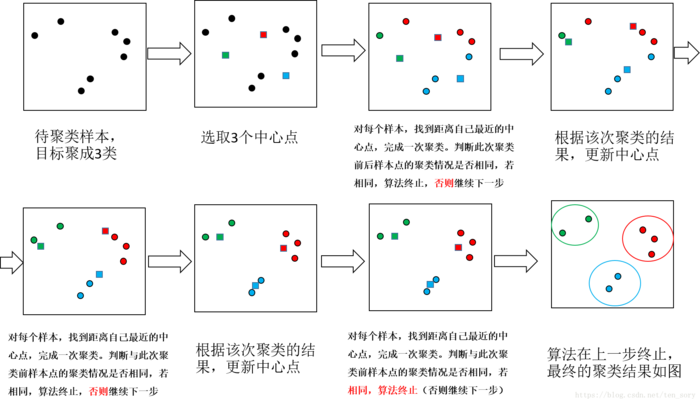
　　如果我们想直接求上式的最小值并不容易，这是一个NP难的问题，因此只能采用启发式的迭代方法。K-Means采用的启发式方式很简单，用下面一组图就可以形象的描述。

2.2 K-Means的基本步骤

　　输入：样本集 $D=\{x_1,x_2,...x_m\}$ ，聚类数 $k$，最大迭代次数 $N$。
　　输出：簇划分 $C=\{C_1,C_2,...C_k\}$
　　1、从数据集 $D$ 中随机选择 $k$ 个样本作为初始的 $k$个质心向量：$\{\mu_1,\mu_2,...,\mu_k\}$
　　2、迭代次数  $n=1,2,...,N$
　　　　a) 将簇划分$C$初始化为 $C_t = \varnothing \;\; t =1,2...k$
　　　　b) 计算样本 $x_i (i=1,2...m)$到各个质心向量 $\mu_j(j=1,2,...k)$的距离：$d_{ij} = ||x_i - \mu_j||_2^2$，将 $x_i$ 标记最小的为$d_{ij}$所对应的类别$\lambda_i$。此时更新$C_{\lambda_i} = C_{\lambda_i} \cup \{x_i\}$
　　　　c) 对 $C_{j} (j=1,2,...,k)$中所有的样本点重新计算新的质心 $\mu_j = \frac{1}{|C_j|}\sum\limits_{x \in C_j}x$
　　　　d) 如果所有的 $k$ 个质心向量都没有发生变化，则转到步骤3）
　　3、 输出簇划分 $C=\{C_1,C_2,...C_k\}$

　　流程概况:
　　1、选定要聚类的类别数目k(如上例的k=3类)，选择k个中心点；
　　2、针对每个样本点，找到距离其最近的中心点，距离同一中心点最近的点为一个类，完成一次聚类；
　　3、判断聚类前后的样本点的类别情况是否相同，如果相同，则算法终止，否则进入步骤4；
　　4、针对每个类别中的样本点，计算这些样本点的中心点，当做该类的新的中心点，继续步骤2。

3 质心优化K-Means++

　　$k$ 个初始化的质心的位置选择对最后的聚类结果和运行时间有很大的影响，因此需要选择合适的$k$个质心。如果随机选择，可能导致算法收敛很慢。$K-Means++$算法是对$K-Means$随机初始化质心的方法的优化。
　　$K-Means++$初始化质心策略如下：
　　a) 从输入的数据点集合中随机选择一个点作为第一个聚类中心$\mu_1$
　　b) 对于数据集中的每一个点$x_i$，计算它与已选择的聚类中心中最近聚类中心的距离$D(x_i) = arg\;min||x_i- \mu_r||_2^2\;\;r=1,2,...k_{selected}$
　　c) 选择一个新的数据点作为新的聚类中心，选择的原则是：$D(x)$较大的点，被选取作为聚类中心的概率较大
　　d) 重复b和c直到选择出 $k$ 个聚类质心
　　e) 利用这 $k$ 个质心来作为初始化质心去运行标准的 $K-Means$ 算法

4 距离计算优化elkan K-Means

　　传统$K-Means$算法中，每轮迭代都要计算所有样本点到所有质心的距离，比较的耗时。那么，如何简化对距离的计算？$elkan K-Means$算法就是从这块加以改进。目标是减少不必要的距离的计算。

　　$elkan K-Means$利用了两边之和大于等于第三边，以及两边之差小于第三边的三角形性质，来减少距离的计算。
　　第一种规律是对于一个样本点$x$两个质心$\mu_{j_1}, \mu_{j_2}$。如果预先计算出这两个质心之间的距离$D(j_1,j_2)$，如果发现$2D(x,j_1) \leq D(j_1,j_2)$,立即可知$D(x,j_1) \leq D(x, j_2)$。此时不需再计算$D(x, j_2)$，省了一步距离计算。
　　第二种规律是对于一个样本点$x$和两个质心$\mu_{j_1}, \mu_{j_2}$。可以得到$D(x,j_2) \geq max\{0, D(x,j_1) - D(j_1,j_2)\}$。
利用上边的两个规律，$elkan K-Means$比起传统的$K-Means$迭代速度有很大的提高。但如果样本的特征是稀疏的，有缺失值，这个方法就不使用，此时某些距离无法计算，则不能使用该算法。

5. 大样本优化Mini Batch K-Means

　　在统的$K-Means$算法中，要计算所有的样本点到所有的质心的距离。如果样本量非常大，比如达到10万以上，特征有100以上，此时用传统的$K-Means$算法非常的耗时，就算加上$elkan K-Means$优化也依旧，此时$Mini Batch K-Means$应运而生。

　　$Mini Batch$就是用样本集中的一部分的样本来做传统的$K-Means$，可避免样本量太大的计算难题，算法收敛速度大大加快。此时的代价就是我们的聚类的精确度也会有一些降低。一般来说这个降低的幅度在可以接受的范围之内。
　　在$Mini Batch K-Means$中，我们会选择一个合适的批样本大小$batch size$，我们仅仅用$batch size$个样本来做$K-Means$聚类。那么这$batch size$个样本怎么来的？一般是通过无放回的随机采样得到的。
　　为了增加算法的准确性，我们一般会多跑几次$Mini Batch K-Means$算法，用得到不同的随机采样集来得到聚类簇，选择其中最优的聚类簇。

6. K-Means与KNN

　　$K-Means$是无监督学习的聚类算法，没有样本输出；而$KNN$是监督学习的分类算法，有对应的类别输出。$KNN$基本不需要训练，对测试集里面的点，需找到在训练集中最近的 $k$个点，用这最近的要$k$个点的类别来决定测试点的类别。而$K-Means$则有明显的训练过程，找到$k$个类别的最佳质心，从而决定样本的簇类别。

　当然，两者也有一些相似点，两个算法都包含一个过程，即找出和某一个点最近的点。两者都利用了最近邻(nearest neighbors)的思想。

参考文献

1.K-Means原理解析