我的小程序:
 待办计划:给自己立个小目标吧!
待办计划:给自己立个小目标吧! 说真的,刚开始接触机器学习,一看到带“核”字的算法就头疼(-…-),没高人指引,总觉得理解起来费劲,也不确定理解的对不对。可能是因为这个“核”有点抽象,没有具体形式(形式不确定),操作很风骚。当然到现在也不敢说自己有多理解,只能扯扯目前所理解到的核主成分分析KPCA。
PCA是简单的线性降维的方法,KPCA则是其非线性的扩展,可以挖掘到数据集中的非线性信息。
KPCA的主要过程是:
- 首先将原始数据非线性映射到高维空间;
- 再把第1步中的数据从高维空间投影降维到需要的维数d'
可以看出,KPCA只是比PCA多了一步映射到高维空间的操作,降维的操作是一样的。所以,KPCA最终投影到的超平面也应满足PCA中的最近重构性或最大可分性。于是KPCA最终的投影向量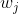 也应满足PCA中的等式(参见:机器学习:降维算法-主成分分析PCA算法两种角度的推导):
也应满足PCA中的等式(参见:机器学习:降维算法-主成分分析PCA算法两种角度的推导):
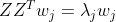 .
.
即:
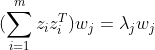 .
.
其中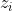 是样本点
是样本点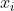 映射到的高维空间中的像。进一步得:
映射到的高维空间中的像。进一步得:
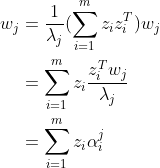 .
.
其中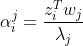 是
是 的第j个分量。
的第j个分量。
假设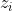 是由原始空间的样本
是由原始空间的样本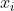 通过映射
通过映射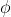 产生,即
产生,即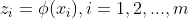 .若映射已知,那么容易求到
.若映射已知,那么容易求到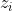 和投影向量
和投影向量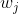 ,问题就解决了。但通常情况下,是不知道
,问题就解决了。但通常情况下,是不知道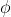 的具体形式的(后面会发现,我们不用知道
的具体形式的(后面会发现,我们不用知道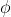 的具体形式一样能求解!)。不管怎样,先表达出
的具体形式一样能求解!)。不管怎样,先表达出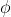 这种映射关系:
这种映射关系:
将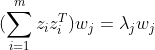 写成:
写成:
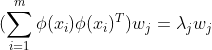 ................................................................(1)
................................................................(1)
将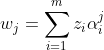 写成:
写成:
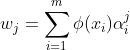 ..................................................................................(2)
..................................................................................(2)
将(2)式代入(1)式得:
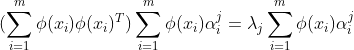 ................................(3)
................................(3)
记:
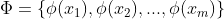 ,
,
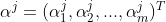 .
.
将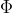 和
和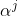 代入(3)式得:
代入(3)式得:
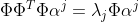 ................................................................................(4)
................................................................................(4)
关键的地方到了,接下来引入核函数:
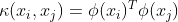 .
.
核函数本质上也就是个函数,跟y=kx没啥区别,特殊之处在于,它的计算结果表达了变量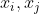 在高维空间的内积
在高维空间的内积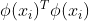 值。就是说,本来是在高维空间(甚至无限维空间)计算的内积
值。就是说,本来是在高维空间(甚至无限维空间)计算的内积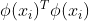 ,可以在原始较低维的空间通过核函数
,可以在原始较低维的空间通过核函数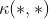 计算得到。
计算得到。
有常见的几种核函数,到底选用哪种核函数,可能需要去尝试,看哪种核函数产生的效果好(比如在KPCA中,就是看哪种核函数带来的降维效果更好)。
之所以引入核函数,可以认为有两方面原因:
- 映射关系
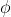 未知;
未知; - 映射到的高维空间维数可能非常高(甚至无限维),在高维空间计算
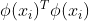 开销太大,十分困难。
开销太大,十分困难。
核函数对应的核矩阵为:
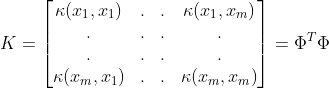 .
.
(4)式两边左乘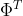 得:
得:
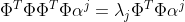 ,
,
把核矩阵K代入上式,可得:
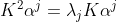 :
:
两边去掉K,得:
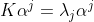 .
.
(这里还是没搞清楚,为什么能直接去掉K,理论上K是可逆矩阵时才能直接消去。但核函数确定的核矩阵只要求是半正定的,半正定矩阵又不一定是可逆的。这里去掉K的依据是什么?望博友指点。)
可以看到,通过核函数的这一波操作,原始空间到高维空间的映射变得无形了,最终得到的式子并没有看到映射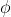 的影子,这就是“核”操作的风骚之处。我们不知道映射
的影子,这就是“核”操作的风骚之处。我们不知道映射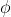 的具体形式,我们也不用知道它的形式。
的具体形式,我们也不用知道它的形式。
显然,上式是特征分解问题,取K的最大的d'个特征值对应的特征向量即可。
对于新样本x,其投影后第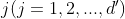 维坐标为:
维坐标为:
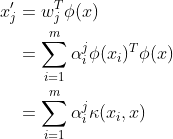 .
.
可以看到,KPCA需要对所有样本求和,计算开销还是挺大的。
 待办计划:给自己立个小目标吧!
待办计划:给自己立个小目标吧!
参考资料:周志华《机器学习》
参考博文:
核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推导过程
机器学习:核函数和核矩阵简介
相关博文:机器学习:降维算法-主成分分析PCA算法两种角度的推导