机器学习学习笔记降维与度量学习

降维与度量学习

k近邻学习(kNN)

k-Nearest Neighbor，k近邻学习是一种常用的监督学习方法。

工作机制

给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个邻居的信息来进行预测，通常，在分类任务中可使用投票法（选择这k个样本中出现最多的类别标记作为预测结果），在回归任务中可使用平均法（将这k个样本的实值输出标记的平均值作为预测结果）。
另外，还可以基于距离远近进行加权或加权投票，距离越近的样本权重越大。
这里的距离，跟聚类的距离是一个距离，感觉用距离的话，更加形象一点，但有的时候转不过来弯- -。
这里将k近邻学习概括起来，就一句话，近朱者赤，近墨者黑，你跟测试样本越近，就越可能是一个类。
注意，这里要理解，测试样本就是一个样本，我们需要得出这个样本的标记（或者输出标记的平均值），就靠与ta靠近的这k个训练样本，他们决定了测试样本的标记到底是什么。
看到这里，你一下子就能知道这个算法的特点，就是根本不需要进行显式的训练，就是不需要花费时间来进行训练，有这样的特点的学习算法，就称之为懒惰学习，反之，则成为急切学习。

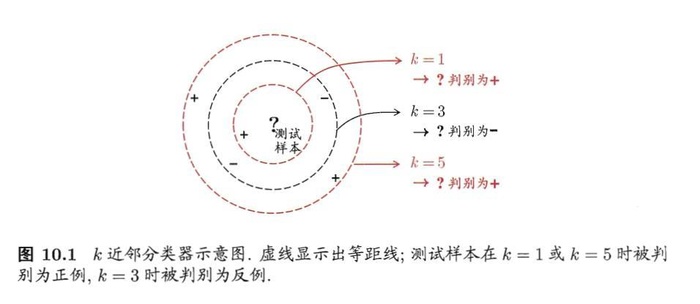
看上面这个图，从近到远，依次选择1 3 5，根据投票法进行分类，得到的结果竟然不同，所以呢，这个算法，k值很重要，起到决定性的影响。

不过我感觉，这个算法的好坏，错误率的高低，取决于距离度量算法- -。

计算错误率

再看一下下面这个讨论

根据这个，k近邻学习，如果是临时性创建分类或者回归，并且精度不要求太精准的话（用的次数越多，精度越高），可以使用，不过有一点需要注意，就是在维度高，数据量小，密度小的时候，错误率会变高。

低维嵌入

当数据的维度变高时，计算量几何增长，使得运算变得困难，不易得出结果（这种情况称为维数灾难）。

一个重要的解决途径就是降维（维数化简）。

降维

通过某种数学变换将原始高维属性空间转变为一个低维子空间，在这个子空间中样本密度大幅提高，距离计算也变得更为容易。
当然，这个降维其实也有他的理论依据，不然能随随便便降么- -
很多时候，人们或者计算机搜集到的数据样本虽然是高维的，但是跟学习任务相关的也许仅仅是某个低维分布，比如你在做图像处理的时候，我们只需要判断有几个独立的物体，这个时候只需要将图片计算阈值，进行二值处理即可，即降维（忽略颜色）。

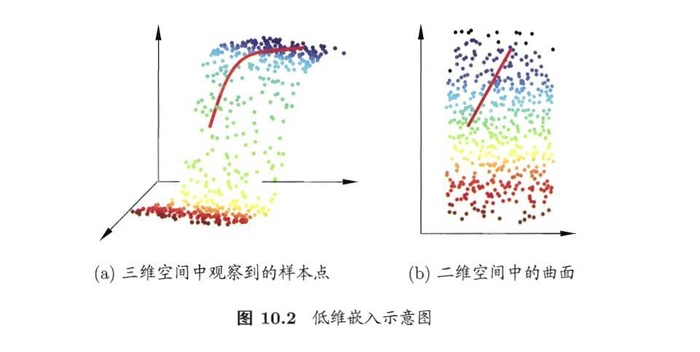
多维缩放(MDS)

在现实应用中为了有效降维，往往仅需要降维后的距离与原始空间中的距离尽可能接近，而不必严格相等。

算法流程

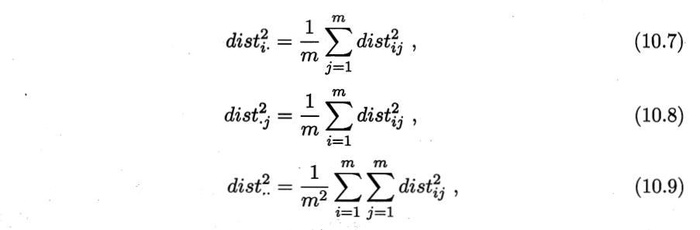
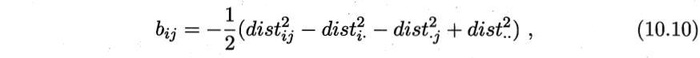
主成分分析(PCA)

PCA的数学原理

算法流程