- 本文来自《Python数据分析从入门到精通》-明日科技编著
- 机器学习顾名思义就是让机器(计算机)模拟人类学习,有效提高工作效率。Python提供的第三方库Scikit-Learn融入了大量的数学模型算法,使得数据分析、机器学习变得简单高效。
- 由于本书以数据处理和数据分析为主,而非机器学习,所以对于Scikit-Learn的相关技术只做简单讲解,主要包括Scikit-Learn简介、安装,以及常用的线性回归模型最小二乘法回归、岭回归、支持向量机和聚类。
10.1 Scikit-Learn简介
- Scikit-Learn(简称SKlearn)是Python的第三方模块,它是机器学习领域中知名的Python模块之一,它对常用的机器学习算法进行了封装,包括回归(Regression)、降维(Dimensionality Reduction)、分类(Classfication)和聚类(Clustering)四大机器学习算法。Scikit-Learn具有以下特点。
- 简单高效的数据挖掘和数据分析工具。
- 让每个人能够在复杂环境中重复使用。
- Scikit-Learn是Scipy模块的扩展,是建立在NumPy和Matplotlib模块的基础上的。利用这几大模块的优势,可以大大提高机器学习的效率。
- 开源,采用BSD协议,可用于商业。
10.2 安装Scikit-Learn
- Scikit-Learn安装要求如下:
- Python版本:高于2.7
- NumPy版本:高于1.10.2
- Scipy版本:高于0.13.3
- 如果已经安装NumPy和Scipy,那么安装Scikit-Learn最简单方法是使用pip工具安装。安装命令如下:
pip install -U scikit-learn -i https://pypi.tuna.tsinghua.edu.cn/simpl
- 这里需要注意:尽量选择安装0.21.2版本,否则运行程序可能出现因为模块版本不适合而导致程序出现错误提示——“找不到只当的模块”。
10.3 线性模型
- Scikit-Learn已经为我们设计好了线性模型(sklearn.linear_model),在程序中直接调用即可,无须编写过多代码就可以轻松实现线性回归分析。首先了解一下线性回归分析。
- 在线性回归中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析;如果线性回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归。
- 在Python中,无须理会繁琐的线性回归求解数学过程,直接使用Scikit-Learn的linear_model模块就可以实现线性回归分析。linear_model模块提供了很多线性模型,包括最小二乘法回归、岭回归、Lasso、贝叶斯回归等。本节主要介绍最小二乘法会u给i和岭回归。
- 首先导入linear_model模块,程序代码如下:
from sklearn import linear_model
- 导入linear_model模块后,在程序中就可以使用相关函数实现线性回归分析。
10.3.1 最小二乘法回归
- 线性回顾是数据挖掘中的基础算法之一,线性回归的思想其实就是解一组方程,得到回归系数,不过在出席那误差项之后,方程的解法就存在了改变,一般用最小二乘法进行计算,所谓“二乘”就是平方的意思,最小二乘法也称最小平方和,其目的是通过最小化误差的平方和,使得预测值与真值无限接近。
- linear_model模块的LinearRegression()函数用于实现最小二乘法回归。LinearRegression()函数拟合一个带有回归系数的线性模型,使得真实数据和预测数据(估计值)之间的残差平方和最小,与真实数据无限接近。LinearRegression()函数语法如下:
linear_model.LinearRegression(fit_intercept=True,normalize=False,copy_X=True,n_jobs=None)
- fit_intercept:布尔型值,是否需要计算截距,默认值为True
- normalize:布尔型值,是否需要标准化,默认值为False,与参数fit_intercept有关。当fit_intercept参数值为False时,将忽略该参数;当fit_intercept参数值为True时,则回归前对回归量X进行归一化(标准化)处理,取均值相减,再除以L2范数(L2范数是指向量各元素的平方和然后开方)。
- copy_X:布尔型值,选择是否复制X数据,默认值为True,如果值为False,则覆盖X数据。
- n_jobs:整型,代表CPU工作效率的核数,默认值为1,-1表示跟CPU核数一致。coef_:数组或形状,表示线性回归分析的回归系数。intercept_:数组,表示截距。
- 主要方法:
- fit(X,y,sample_weight=None):拟合线性模型。
- predict(X):使用线性模型返回预测数据。
- score(X,y,sample_weight=None):返回预测的确定系数R^2
- LinearRegression()函数调用fit()方法来拟合数组X、y,并且将线性模型的回归系数存储在其成员变量coef_属性中。
智能预测房价(01)
- 智能预测房价,假设某地房屋面积和价格概念性如图10.2所示,下面使用LinearRegression()函数预测面积为170平方米的房屋的单价。

- 程序代码如下:
from sklearn import linear_model
import numpy as np
x=np.array([[1,56],[2,104],[3,156],[4,200],[5,250],[6,300]])
y=np.array([7800,9000,9200,10000,11000,12000])
clf = linear_model.LinearRegression()
clf.fit (x,y) #拟合线性模型
k=clf.coef_ #回归系数
b=clf.intercept_ #截距
x0=np.array([[7,170]])
#通过给定的x0预测y0,y0=截距+X值*回归系数
y0=clf.predict(x0) #预测值
print('回归系数:',k)
print('截距:',b)
print('预测值:',y0)
回归系数: [1853.37423313 -21.7791411 ]
截距: 7215.950920245396
预测值: [16487.11656442]
10.3.2 岭回归
- 岭回归是在最小二乘法回归基础上,加上了对表示回归系数的L2
范数约束。岭回归是缩减法的一种,相对于对回归系数的大小施加了限制。岭回归主要使用linear_model模块的Ridge()函数实现。语法如下:
linear_model.Ridge(alpha=1.0, fit_intercept=True,normalize=False,copy_X=True,max_iter=None,tol=0.001,solver="auto",random_state=None)
- alpha:权重。
- fit_intercept:布尔型值,是否需要计算截距,默认值为True。
- normalize:输入的样本特征归一化,默认值为False。
- copy_X:复制或者重写。
- max_iter:最大迭代次数。
- tol:浮点数,控制求解的精度。
- solver:求解器,其值包括auto、svd、cholesky、sparse_cg和lsqr,默认值为auto
- coef_:数组或形状,表示线性回归分析的回归结果。
- 主要方法
- fit(X,y):拟合线性模型。
- predict(X):使用线性模型返回预测数据。
- Ridg()函数使用fit()方法将线性回归模型的回归系数存储在其成员变量coef_属性中。
使用岭回归函数实现智能预测房价(02)
from sklearn.linear_model import Ridge
import numpy as np
x=np.array([[1,56],[2,104],[3,156],[4,200],[5,250],[6,300]])
y=np.array([7800,9000,9200,10000,11000,12000])
clf = Ridge(alpha=1.0)
clf.fit(x, y)
k=clf.coef_ #回归系数
b=clf.intercept_ #截距
x0=np.array([[7,170]])
#通过给定的x0预测y0,y0=截距+X值*斜率
y0=clf.predict(x0) #预测值
print('回归系数:',k)
print('截距:',b)
print('预测值:',y0)
回归系数: [10.00932795 16.11613094]
截距: 6935.001421210872
预测值: [9744.80897725]
10.4 支持向量机
- 支持向量机(SVM)可用于监督学习算法,主要包括分类、回归和异常检测。支持向量分类的方法可以被扩展用作解决回归问题,这个方法被称为支持向量回归。
- 本节介绍支持向量回归函数——LinearSVR()函数。LinearSVR()类是一个支持向量回归的函数,支持向量回归不仅适用于线性模型,还可以用于对数据和特征之间的非线性关系的研究。避免多重共线性问题,从而提高广泛化性能,解决高维问题,语法如下:
sklearn.svm.LinearSVR(epsilon=0.0,tol=0.0001,C=1.0,loss='epsilon_insensitive',fit_intercept=True,intercept_scaling=1.0,dual=True,verbose=0,random_state=None,max_iter=1000)
- epsilon:float类型值,默认值为0.0
- tol:float类型值,终止迭代的标准值,默认值为0.0001
- C:float类型值,罚项参数,该参数越大,使用的正则化越少,默认值为1.0
- loss:string类型值,损失函数,该参数有以下两种选项:epsilon_insensitive:默认值,不敏感损失(标准SVR)是L1损失。squared_epsilon_insensitive:平方不敏感损失是L2损失。
- fit_intercept:boolean类型值,是否计算此模型的截距。如果设置值为False,则不会在计算中使用截距(即数据预计已经居中)。默认值为True。
- intercept_scaling:float类型值,当fit_intercept为True时,实例向量x变为[x,self.intercept_scaling]。此时相当于添加了一个特征,该特征将对所有实例都是常数值。
- dual:boolean类型值,选择算法以解决对偶或原始优化问题。当设置值为True时,可解决对偶问题;当设置值为False时,可解决原始问题。默认值为True。
- verbose:int类型值,是否开启verbose输出,默认值为0
- random_state:int类型值,随机数生成器的种子,用于在数据清洗时使用。默认值为None。
- max_iter:int类型值,要运用的最大迭代次数。默认值为0
- 两个重要的属性:
– coef_:赋予特征的权重,返回array数据类型。
– intercept_:决策函数中的常量,返回array数据类型。
波士顿房价预测
- 通过Scikit-Learn自带的数据集“波士顿房价”,实现房价预测,程序代码如下:
from sklearn.svm import LinearSVR # 导入线性回归类
from sklearn.datasets import load_boston # 导入加载波士顿数据集
from pandas import DataFrame # 导入DataFrame
boston = load_boston() # 创建加载波士顿数据对象
# 将波士顿房价数据创建为DataFrame对象
df = DataFrame(boston.data, columns=boston.feature_names)
df
df.insert(0,'target',boston.target) # 将价格添加至DataFrame对象中
df
data_mean = df.mean() # 获取每一列的平均值
data_std = df.std() # 获取标准偏差
data_train = (df - data_mean) / data_std # 数据标准化
data_train
x_train = data_train[boston.feature_names].values # 特征数据,feature_names就是上图中除了target列之外的其他列的数值
y_train = data_train['target'].values # 目标数据
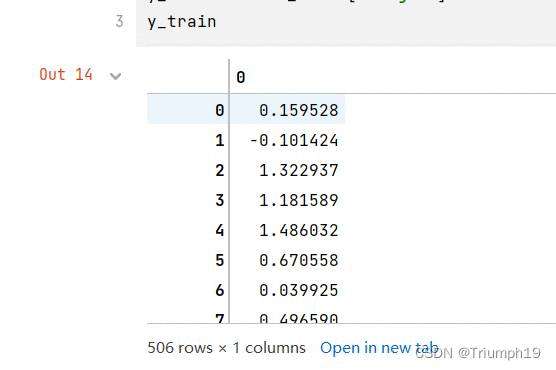
也是使用列表的方式直接提取所需列的数值,比如data_train[[‘target’,‘ZN’]]…values就是获取target列和ZN列的数据;data_train[[‘target’:‘ZN’]]…values是获取从targer到ZN一共三列数据。
#%%
linearsvr = LinearSVR(C=0.1) # 创建LinearSVR()对象
linearsvr.fit(x_train, y_train) # 训练模型
# 预测,并还原结果
x = ((df[boston.feature_names] - data_mean[boston.feature_names]) / data_std[boston.feature_names]).values
x
# 添加预测房价的信息列
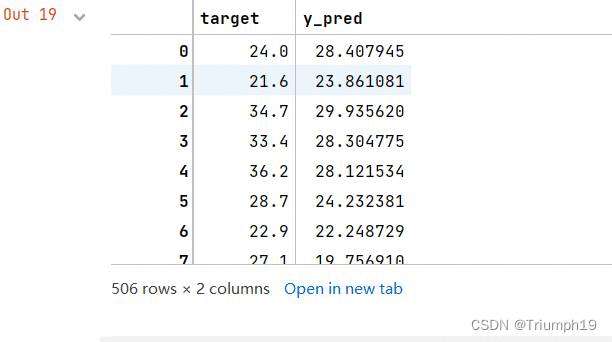
df[u'y_pred'] = linearsvr.predict(x) * data_std['target'] + data_mean['target'] #这是还原结果的代码
df[['target','y_pred']] #提取出真是价格和预测价格
10.5 聚类
10.5.1 什么是聚类
- 聚类类似于分类,不同的是聚类所要求划分的类是未知的,也就是说不知道应该属于哪类,而是通过一定的算法自动分类。在实际应用中,聚类是一个将在某些方面相似的数据进行分类组织的过程(简单地说就是将相似数据聚在一起),其示意图如图10.3和图10.4所示。

- 聚类主要应用领域如下。
- 商业:聚类分析被用来发现不同的客户群,并且通过购买模式刻画不同客户群的特征。
- 生物:聚类分析被用来对动植物分类和对基因进行分类,获取对种群固有结构的认识。
- 保险行业:聚类分析通过一个高的平均消费来鉴定保险单持有者的分组,同时根据住宅类型、价值和地理位置来判断一个城市的房产分组。
- 互联网:聚类分析被用来在网上进行文档归类。
- 电子商务:聚类分析在电子商务网站数据挖掘中也是很重要的一个方面,通过分组聚类出具有相似浏览行为的客户,并分析客户的共同特征,可以更好地帮助电商了解自己的客户,向客户提供更合适的服务。
10.5.2 聚类算法
- k-means算法是一种聚类算法,它是一种无监督学习算法,目的是将相似的对象归到一个簇中。簇内的对象越相似,聚类的效果越好。
- 传统的聚类包括划分方法、层次方法、基于密度方法、基于网格方法和基于模型方法。本节主要介绍k-means聚类算法,它是划分方法中较典型的一种,也可以称为k均值聚类算法。下面介绍什么是k均值聚类以及相关算法。
1.k-means聚类
- k-means聚类也称为k均值聚类,是著名的划分聚类的算法,由于简洁和高效使得它成为所有聚类算法中应用最广泛的一种。k均值聚类是给定一个数据点集合和需要的聚类数目k,k由用户指定,k均值算法根据某个距离函数反复把数据分入k个聚类中。
2.算法
- 随机选取k个点作为初始质心(质心即簇中所有点的中心),然后将数据集中的每个点分配到一个簇中,具体来讲,为每个点找距其最近的质心,并将其分配给该质心所对应的簇。这一步完成之后,将每个簇的质心更新为该簇所有点的平均值。这个过程将不断重复直到满足某个终止条件。终止条件可以是以下任何一个。
- 没有(或最小数目)对象被重新分配给不同的聚类。
- 没有(或最小数目)聚类中心再发生变化。
- 误差平方和局部最小。
- 伪代码:
"""
创建k个点作为起始质心,可以随机选择(位于数据边界内)
当任何一个点的簇分配结果发生变化时(初始化为True)
对数据集中每个数据点,重新分配质心
对每个质心
计算质心和数据点之间的距离
将数据点分配到距其最近的簇
对每一个簇,计算簇中所有点的均值并将均值作为新的质心
"""
- 通过以上代码介绍相信读者对k-means聚类算法已经有了初步的认识,而在Python中应用该算法无需手动编写代码,因为Python第三方模块Scikit-Learn已经帮我们写好了,在性能和稳定性上比自己写的好得多,只需在程序中调用即可,没必要自己造轮子。
10.5.3 聚类模块
- Scikit-Learn的cluster模块用于聚类分析,该模块提供了很多聚类算法,下面主要介绍KMeans方法,该方法通过k-means聚类算法实现聚类分析。
- 首先导入sklearn-cluster模块的KMeans方法,程序代码如下:
from sklearn.cluster import KMeans
- 接下来,在程序中就可以使用KMeans()方法了。KMeans()方法的语法如下:
KMeans(n_clusters=8,init='k-means++',n_init=10,max_iter=300,tol=1e-4,precompute_distances='auto',verbose=0,random_state=None,copy_x=True,n——jobs=None,algorithm='auto')
- n_cluster:整型,默认值为8,是生成的聚类数,即产生的质心(centroid)数。
- init:参数值为k-means++、random或者传递一个数值向量。默认值为k-means++。
– k-means++:用一种特殊的方法选定初始质心从而加速迭代过程的收敛。
– random:随机从训练数据中选取初始质心。如果传递数组类型,则应该是shape(n_clusters,n_features)的形式,并给出初始质心。 - n_init:整型,默认值为10,用不同的质心初始化值运行算法的次数。
- max_iter:整型,默认值为300,每执行一次k-means算法的最大迭代次数。
- tol:浮点型,默认值为1e-4(科学计数法,即1乘10的-4次方),控制求解的精度。
- precompute_distances:参数值为auto、True或者False。用于预先计算距离,计算速度更快当占用更多内存。
– auto:如果样本数乘以聚类数大于12e6(即12乘10的6次方),则不预先计算距离。
– True:总是预先计算距离。
– False:永远不预先估计距离。 - verbose:整型,默认值为0,冗长的模式。
- random_state:整型或随机数组类型。用于初始化质心的生成器(generator)。如果值为一个整数,则确定一个种子(seed)。默认值为NumPy的随机数生成器。
- copy_x:布尔型,默认值为True。如果值为True,则原始数据不会改变;如果值为False,则会直接在原始数据上做修改,并在函数返回时将其还原。但是在计算过程中由于有对数据的均值的加减运算,所以数据返回后,原始数据同计算数据可能会有细小差别。
- n_jobs:整型,指定计算所用的进程数。如果值为-1,则用所有的CPU进行运算;如果值为1,则不进行并行计算,这样方便调试;如果值小于-1,则用到的CPU数为(n_cpus+1+n_jobs),例如n_jobs=-2,则用到的CPU数为总CPU数减1。
- algorithm:表示k-means算法法则,参数值为auto、full或elkan,默认值为auto。
- 主要属性:
- cluster_centers_:返回数组,表示分类簇的均值向量。
- labels_:返回数组,表示每个样本数据所属的类别标记。
- inertia_:返回数组,表示每个样本数据距离它们各自最近簇的中心之和。
- fit(X[,y]):计算k-means聚类。
- fit_predict(X[,y]):计算簇质心并给每个样本数据预测类别。
- predict(X):给每个样本估计最接近的簇。
- score(X[,y]):计算聚类误差。
对一组数据聚类。
import numpy as np
from sklearn.cluster import KMeans
X=np.array([[1,10],[1,11],[1,12],[3,20],[3,23],[3,21],[3,25]])
kmodel = KMeans(n_clusters = 2) #调用KMeans方法实现聚类(两类)
y_pred=kmodel.fit_predict(X) #预测类别
print('预测类别:',y_pred)
print('分类簇的均值向量:','\n',kmodel.cluster_centers_)
print('类别标记:',kmodel.labels_)
预测类别: [1 1 1 0 0 0 0]
分类簇的均值向量:
[[ 3. 22.25]
[ 1. 11. ]]
类别标记: [1 1 1 0 0 0 0]
10.5.4 聚类数据生成器
- 10.5.3节列举了一个简单的聚类示例,但是聚类效果并不明显。本节生成了专门的聚类算法的测试数据,可以更好地诠释聚类算法,展示聚类效果。
- Scikit-Learn的make_blobs()方法用于生成聚类算法的测试数据,直观地说,make_blobs()方法可以根据用户指定的特征数量、中心点数量、范围等生成几类数据,这些数据可用于测试聚类算法的效果。
- make_blobs()方法的语法如下:
sklearn.datasets.make_blobs(n_samples=100,n_features=2,centers=3,cluster_std=1.0,center_box=(-10.0,10.0),shuffle=True,random_state=None)
- n_samples:待生成的样本的总数。
- n_features:每个样本的特征数。
- centers:类别数。
- cluter_std:每个类别的方差,例如,生成两类数据,其中一类比另一类具有更大的方差,可以将cluster_std设置为[1.0,3.0]。
生成用于聚类的测试数据
- 生成用于聚类的数据(500个样本,每个样本有两个特征),程序代码如下:
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
x,y = make_blobs(n_samples=500, n_features=2, centers=3)
- 接下来,通过KMeans()方法对测试数据进行聚类,程序代码如下:
from sklearn.cluster import KMeans
y_pred = KMeans(n_clusters=4, random_state=9).fit_predict(x)
plt.scatter(x[:, 0], x[:, 1], c=y_pred)
plt.show()
- 运行程序,效果如下:
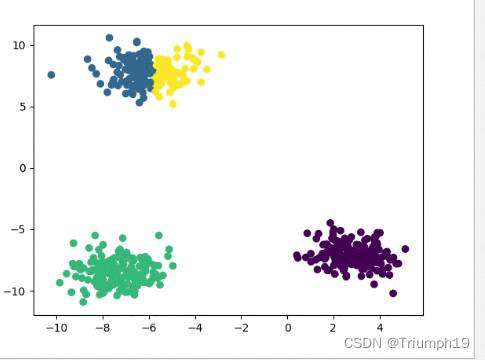
- 从分析结果得知:相似的数据聚在一起,分成了4堆,也就是4类,并以颜色显示,看上去清晰直观。
10.6 小结
- 通过本章的学习,能够了解机器学习Scikit-Learn模块,该模块包含大量的算法模型,本章仅介绍了几个常用模型并结合快速示例,力求使读者能够轻松上手,快速理解相关模型的用法,并为后期学习数据分析与预测项目打下良好的基础。











 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有