一、排序简介
排序算法大体可分为两种:
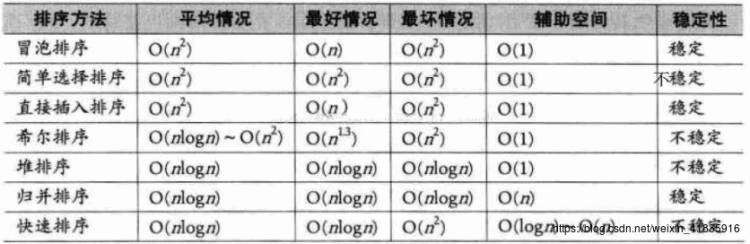
1、比较排序,时间复杂度O(nlogn) ~ O(n^2),主要有:冒泡排序,选择排序,插入排序,归并排序,堆排序,快速排序等。
2、非比较排序,时间复杂度可以达到O(n),主要有:计数排序,基数排序,桶排序等。
二、冒泡排序法
算法思路:
1、比较相邻的元素。如果第一个比第二个大,就交换它们两个;
2、对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
3、针对所有的元素重复以上的步骤,除了最后一个;
4、重复步骤1~3,直到排序完成。

代码:
public class
{
public static void main(String[] args) {
int array[] = {1,2,4,3,9,7,8,6};
for( int i &#61; 0;i <array.length - 1;i&#43;&#43; ){
for( int j &#61; 0;j <array.length - i - 1;j&#43;&#43; ){
if( array[j] > array[j&#43;1] ){
int temp &#61; array[j];
array[j] &#61; array[j&#43;1];
array[j&#43;1] &#61; temp;
}
}
}
for( int i &#61; 0 ; i <array.length ; i&#43;&#43; ){
System.out.print(array[i]&#43;" ");
}
}
}
//运行结果:
//1 2 3 4 6 7 8 9
三、选择排序
算法思路&#xff1a;
首先在未排序序列中找到最小&#xff08;大&#xff09;元素&#xff0c;存放到排序序列的起始位置&#xff0c;然后&#xff0c;再从剩余未排序元素中继续寻找最小&#xff08;大&#xff09;元素&#xff0c;然后放到已排序序列的末尾。以此类推&#xff0c;直到所有元素均排序完毕。

代码&#xff1a;
public class XuanZePaiXu {
public static void main(String[] args) {
int minIndex &#61; 0;
int temp &#61; 0;
int array[] &#61; {1,2,4,3,9,7,8,6};
for(int i &#61; 0;i <array.length;i&#43;&#43;){
minIndex &#61; i; //先假设最开始的元素为最小的元素
for( int j &#61; i &#43; 1;j <array.length;j&#43;&#43; ){
if( array[j] <array[minIndex] ){ // 寻找最小的数
minIndex &#61; j; // 将最小数的索引保存
}
}
temp &#61; array[minIndex]; //将此轮的最小元素和最开始的元素交换
array[minIndex] &#61; array[i];
array[i] &#61; temp;
}
for( int i &#61; 0;i <array.length;i&#43;&#43; ){
System.out.print(array[i]&#43;" ");
}
}
}
//运行结果&#xff1a;
//1 2 3 4 6 7 8 9
四、插入排序
算法思路&#xff1a;
1、从第一个元素开始&#xff0c;该元素可以认为已经被排序&#xff1b;
2、取出下一个元素&#xff0c;在已经排序的元素序列中从后向前扫描&#xff1b;
3、如果该元素&#xff08;已排序&#xff09;大于新元素&#xff0c;将该元素移到下一位置&#xff1b;
4、重复步骤3&#xff0c;直到找到已排序的元素小于或者等于新元素的位置&#xff1b;
5、将新元素插入到该位置后&#xff1b;
6、重复步骤2~5。

代码&#xff1a;
public class ChaRuPaiXu {
public static void main(String[] args) {
int array[] &#61; {1,2,4,3,9,7,8,6};
int index &#61; 0;
int current &#61; 0;
for (int i &#61; 1; i
current &#61; array[i]; //表示当前取到的扑克牌
while (index >&#61; 0 && array[index] > current) { //如果左边的排比取到的排大则右移
array[index &#43; 1] &#61; array[index];
index--;
}
array[index &#43; 1] &#61; current; //直到该手牌比抓到的牌小(或二者相等)&#xff0c;将抓到的牌插入到该手牌右边
}
for( int i &#61; 0 ; i
}
}
}
//运行结果&#xff1a;
//1 2 3 4 6 7 8 9
五、希尔排序
算法思路&#xff1a;
1、选择一个增量序列t1&#xff0c;t2&#xff0c;…&#xff0c;tk&#xff0c;其中ti>tj&#xff0c;tk&#61;1&#xff1b;
2、按增量序列个数k&#xff0c;对序列进行k 趟排序&#xff1b;
3、每趟排序&#xff0c;根据对应的增量ti&#xff0c;将待排序列分割成若干长度为m 的子序列&#xff0c;分别对各子表进行直接插入排序。仅增量因子为1 时&#xff0c;整个序列作为一个表来处理&#xff0c;表长度即为整个序列的长度

常用的h序列由Knuth提出&#xff0c;该序列从1开始&#xff0c;通过如下公式产生&#xff1a;
h &#61; 3 * h &#43;1
反过来程序需要反向计算h序列&#xff0c;应该使用
h &#61; ( h - 1 ) / 3
代码&#xff1a;
public class XiErPaiXu {
public static void main(String[] args) {
int array[] &#61; {1,2,4,3,9,7,8,6};
int h &#61; 0;
int length &#61; array.length;
while( h <&#61; length ){ //计算首次步长
h &#61; 3 * h &#43; 1;
}
while( h >&#61; 1 ){
for( int i &#61; h;i
int get &#61; array[i]; //当前元素
while( j >&#61; 0 && array[j] > get ){ //左边的比当前大&#xff0c;则左边的往右边挪动
array[j&#43;h] &#61; array[j];
j &#61; j - h;
}
array[j &#43; h] &#61; get; //挪动完了之后把当前元素放进去
}
h &#61; ( h - 1 ) / 3;
}
for( int i &#61; 0 ; i
}
}
}
//运行结果&#xff1a;
//1 2 3 4 6 7 8 9
六、归并排序
算法思路&#xff1a;
该算法是采用分治法&#xff08;Divide and Conquer&#xff09;的一个非常典型的应用。将已有序的子序列合并&#xff0c;得到完全有序的序列&#xff1b;即先使每个子序列有序&#xff0c;再使子序列段间有序。若将两个有序表合并成一个有序表&#xff0c;称为2-路归并。
1、把长度为n的输入序列分成两个长度为n/2的子序列&#xff1b;
2、对这两个子序列分别采用归并排序&#xff1b;
3、将两个排序好的子序列合并成一个最终的排序序列。

代码&#xff1a;
/*
k表示最终i和j比较之后最终需要放的位置
i和j用来表示当前需要考虑的元素
left表示最左边的元素
right表示最右边的元素
middle表示中间位置元素&#xff0c;放在第一个已经排好序的数组的最后一个位置
*/
public class GuiBingPaiXu {
/*******************测试************************/
public static void main(String[] args) {
int[] nums &#61; { 2, 7, 8, 3, 1, 6, 9, 0, 5, 4 , 9 , 19 ,12,16,14,12,22,33 };
mergeSort(nums , 0 , nums.length - 1 );
System.out.println(Arrays.toString(nums));
}
/********************算法************************/
/*
arr&#xff1a;要处理的数组
l&#xff1a;开始位置
r&#xff1a;结束位置
递归对arr[ l ... r ]范围的元素进行排序
*/
private static void mergeSort(int[] arr,int left,int right){
if( right - left <&#61; 10 ){ //当数据很少的时候使用插入排序算法
ChaRuPaiXu.ChaRuPaiXuFa2( arr , left ,right);
return;
}
int middle &#61; ( left &#43; right ) / 2; //计算中点位置
mergeSort( arr , left , middle ); //不断地对数组的左半边进行对边分
mergeSort( arr , middle&#43;1 , right ); //不断地对数组的右半边进行对半分
if( arr[middle] > arr[middle&#43;1] ) //当左边最大的元素都比右边最小的元素还小的时候就不用归并了
merge( arr , left , middle , right ); //最后将已经分好的数组进行归并
}
//将arr[ l... mid ]和arr[ mid ... r ]两部分进行归并
/*
|2, 7, 8, 3, 1 | 6, 9, 0, 5, 4|
*/
private static void merge(int[] arr, int left, int mid, int right) {
int arr1[] &#61; new int[ right - left &#43; 1 ]; //定义临时数组
for( int i &#61; left ; i <&#61; right ; i&#43;&#43; ) //将数组的元素全部复制到新建的临时数组中
arr1[ i - left ] &#61; arr[ i ];
int i &#61; left;
int j &#61; mid &#43; 1; //定义两个索引
for( int k &#61; left;k <&#61; right ; k&#43;&#43;){
if( i > mid ) //如果左边都比较完了
{
arr[ k ] &#61; arr1[ j - left ]; //直接将右边的元素都放进去
j&#43;&#43;;
}
else if( j > right ){ //右边都比较完了
arr[ k ] &#61; arr1 [i - left ]; //直接将左边的元素放进去
i&#43;&#43;;
}
else if( arr1[ i-left ]
i&#43;&#43;;
}
else
{
arr[ k ] &#61; arr1[ j - left];
j&#43;&#43;;
}
}
}
}
七、快速排序
算法思路&#xff1a;
通过一趟排序将待排记录分隔成独立的两部分&#xff0c;其中一部分记录的关键字均比另一部分的关键字小&#xff0c;则可分别对这两部分记录继续进行排序&#xff0c;以达到整个序列有序。
快速排序使用分治法来把一个串&#xff08;list&#xff09;分为两个子串&#xff08;sub-lists&#xff09;。
1、从数列中挑出一个元素&#xff0c;称为 “基准”&#xff08;pivot&#xff09;&#xff1b;
2、重新排序数列&#xff0c;所有元素比基准值小的摆放在基准前面&#xff0c;所有元素比基准值大的摆在基准的后面&#xff08;相同的数可以到任一边&#xff09;。在这个分区退出之后&#xff0c;该基准就处于数列的中间位置。这个称为分区&#xff08;partition&#xff09;操作&#xff1b;
3、递归地&#xff08;recursive&#xff09;把小于基准值元素的子数列和大于基准值元素的子数列排序。

代码&#xff1a;
public class KuaiSuPaiXu {
public static void main(String[] args){
int array[] &#61; {1,2,4,3,9,7,8,6};
quickSort(array,0,array.length-1);
for( int i &#61; 0 ; i
}
}
private static void quickSort(int[] arr,int l,int r){
if( l >&#61; r ) return;
int p &#61; partition(arr,l,r); //找到中间位置
quickSort(arr,l,p-1);
quickSort(arr,p&#43;1,r);
}
private static int partition(int[] arr,int l,int r){
int v &#61; arr[l]; //取出第一个元素
int j &#61; l; //j表示小于第一个元素和大于第一个元素的分界点
for( int i &#61; l &#43; 1;i <&#61; r;i&#43;&#43; ){
//将所有小于第一个元素的值的元素全部都放到它的左边
if( arr[i]
swap(arr,i,j&#43;1);
j&#43;&#43;;
}
}
swap(arr,l,j); //将第一个元素和中间的元素进行交换
return j;
}
}
//运行结果&#xff1a;
//1 2 3 4 6 7 8 9
八、堆排序
算法思路&#xff1a;
堆排序&#xff08;Heapsort&#xff09;是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构&#xff0c;并同时满足堆积的性质&#xff1a;即子结点的键值或索引总是小于&#xff08;或者大于&#xff09;它的父节点。

最大堆要求节点的元素都要不小于其孩子&#xff0c;最小堆要求节点元素都不大于其左右孩子
那么处于最大堆的根节点的元素一定是这个堆中的最大值.
public class DuiPaiXu {
public static void main(String[] args) {
int A[]&#61;{49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
HeapSort(A, A.length);
System.out.println(Arrays.toString(A));
}
public static void Swap(int A[], int i, int j)
{
int temp &#61; A[i];
A[i] &#61; A[j];
A[j] &#61; temp;
}
public static void Heapify(int A[], int i, int size) // 从A[i]向下进行堆调整
{
int left_child &#61; 2 * i &#43; 1; // 左孩子索引
int right_child &#61; 2 * i &#43; 2; // 右孩子索引
int max &#61; i; // 选出当前结点与其左右孩子三者之中的最大值
if (left_child
max &#61; left_child;
if (right_child
max &#61; right_child;
if (max !&#61; i)
{
Swap(A, i, max); // 把当前结点和它的最大(直接)子节点进行交换
Heapify(A, max, size); // 递归调用&#xff0c;继续从当前结点向下进行堆调整
}
}
public static int BuildHeap(int A[], int n) // 建堆&#xff0c;时间复杂度O(n)
{
int heap_size &#61; n;
for (int i &#61; heap_size / 2 - 1; i >&#61; 0; i--) // 从每一个非叶结点开始向下进行堆调整
Heapify(A, i, heap_size);
return heap_size;
}
public static void HeapSort(int A[], int n)
{
int heap_size &#61; BuildHeap(A, n); // 建立一个最大堆
while (heap_size > 1) // 堆&#xff08;无序区&#xff09;元素个数大于1&#xff0c;未完成排序
{
// 将堆顶元素与堆的最后一个元素互换&#xff0c;并从堆中去掉最后一个元素
// 此处交换操作很有可能把后面元素的稳定性打乱&#xff0c;所以堆排序是不稳定的排序算法
Swap(A, 0, --heap_size);
Heapify(A, 0, heap_size); // 从新的堆顶元素开始向下进行堆调整&#xff0c;时间复杂度O(logn)
}
}
}
Java面试的完整博客目录如下&#xff1a;Java笔试面试目录


 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有