概率与期望dp

概率

某个事件A发生的可能性的大小，称之为事件A的概率，记作P(A)。

假设某事的所有可能结果有n种，每种结果都是等概率，事件A涵盖其中的m种，那么P(A)=m/n。

例如投掷一枚骰子，点数小于3的概率为2/6=1/3。

如果两个事件A和B所涵盖的结果没有交集，那么P(A或B发生)=P(A)+P(B)

还是掷骰子

P(点数小于3或点数大于4)=2/6+2/6=2/3

如果A和B所涵盖的结果有交集

那么P(A或B发生)=P(A)+P(B)-P(A与B同时发生)

P(点数小于3或点数为偶数)=2/6+3/6-1/6=2/3

记事件B为“事件A不发生”

那么P(A)+P(B)=1，即P(B)=1-P(A)

P(点数不小于3)=1-2/6=2/3

在两个互不干扰的事中，事件A在其中一件事中，事件B在另外一件事中

那么P(A与B同时发生)=P(A)*P(B)

掷两个骰子， P(第一个点数小于3且第二个点数为偶数)=(2/6)×(3/6)=1/6

期望

事件A有多种结果，记其结果的大小为x，那么x的期望值表示事件A的结果的平均大小，记作E(x)。

E(x)=每种结果的大小与其概率的乘积的和。

例如，记掷一枚骰子的点数为x

E(x)=1*(1/6)+2*(1/6)+3*(1/6)+4*(1/6)+5*(1/6)+6*(1/6)=7/2

若c为常数，那么：

E(x+c)=E(x)+c， E(c*x)=c*E(x)

E(x+c)=(1+c)*(1/6)*……*(6+c)*(1/6);

记两个事件的结果分别为x,y

E(x+y)=E(x)+E(y)

例如： E(语文成绩+数学成绩)=E(语文成绩)+E(数学成绩)

可以举一个例子证明是正确的;

若两个事件互相独立， E(x*y)=E(x)*E(y)

E(语文成绩*数学成绩)=E(语文成绩)*E(数学成绩)

概率与期望的计算有一个共同的计算技巧：

若事件所产生的所有方案都是等概率的，那么一些概率与期望即可转化为一个计数问题，算出后再除以总方案数即可。

如求事件符合条件A的概率，则转化为对符合A的方案数的计数问题；若求方案的价值的期望值，则转化为所有方案的价值总和的计数问题。

解释：E（x）=case1*p1+case*p2+case3*p3……+casen*pn,因为是等概率问题，p1=p2=……=pn，因此我们可以把所有case值加起来然后再*p;

概率和期望的计算

概率与期望的计算也经常用的其加法和乘法规则。

尤其是期望的加法规则，在期望的计算中十分常用。 如求最大值与最小值之差的期望，则分别求二者的期望值再作差即可。

乘法规则时，要注意事件是否互相独立

概率与期望还可以通过列方程的方法计算。

有4张卡片，写着0,1,2,3，每次抽出一张并放回，反复抽，抽出0为止。问抽取的次数的期望值。

设抽取次数为x，则：

x=1+x*3/4

x=4

1表示第一次一定需要抽一次，然后对于一个状态，有1/4概率抽到0，那么继续抽取的次数是0，因此为1/4*0，有3/4的概率抽到其余的，需要继续抽，此时期望还是x个，所以就是3/4*x

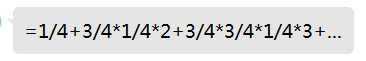
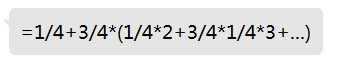
就差不多↑的感觉

BZOJ1867 钉子和小球

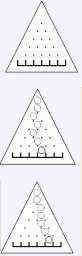
n<=50；

比较简单的概率dp

如果某一个的钉子(x,y)不见了，那么小球垂直下落，就转移到了(x+2,j+1);

设\(f[i][j]\)为小球经过第i行第j列的概率。

$f[1][1]=1 $（即起状态概率为1

\(f[i][j]=f[i-1][j-1] * [(i-1,j-1)有钉子]*1/2 +f[i-1][j] * [(i-1,j)有钉子]*1/2 +f[i-2][j-1] * [(i-2,j-1)没有钉子]\)

\([(i-1,j-1)有钉子]\)可以看做一个bool的0/1数组，有钉子为1，没钉子为0；

至于分数输出，自定义分数数据类型并用gcd化简分数即可。

Bzoj5004 开锁魔法II

有 n 个箱子，每个箱子里有且仅有一把钥匙，每个箱子有且仅有一把钥匙可以将其打开。现在随机打开 m 个箱子，求能够将所有箱子打开的概率。

100组数据， k<=n<=300。

总方案数C~n~^m^

题目约定了每个点的入度和出度均为1，因此最终的图一定是若干个环。每个环都至少选择一个点即可满足要求。求概率，实际上就是求方案数，最后再除以总方案数即可。

预处理出每个环的点数 c[i] 以及其后缀和 sum[i] 。

设$ f[i][j] \(表示前 i 个环中选出 j 个点，满足最终条件每个环都选的方案数。初始化\) f[0][0]=1$ 。

枚举 i 和 前 i 个环选的点数 j 、第 i 个环选的点数 k

可得\(f[i][j]=\sum\limits_{k=1}^{c[i]}f[i-1][j-k]*C^k_{c[i]}\)

BZOJ5091 摘苹果

在花园中有n棵苹果树以及m条双向道路，每条道路的两端连接着两棵不同的苹果树。假设第i棵苹果树连接着di条道路。小Q将会按照以下方式去

采摘苹果：

1.随机移动到一棵苹果树下，移动到第i棵苹果树下的概率为di/2m，但不在此采摘。

2.重复以下操作k次：等概率随机选择一条与当前苹果树相连的一条道路，移动到另一棵苹果树下，假设当前位于第i棵苹果树下，则他会采摘ai个苹果，多次经过同一棵苹果树下会重复采摘。

请计算小Q期望摘到多少苹果。 n,k<=100000,m<=200000

首先证明这是等概率事件：

设\(f[i][j]\)表示进行了i次操作走到j的概率，易知\(f[0][j]=\frac{dj}{2m}\)（从哪个点开始摘1）

然后考虑转移：第一步从起点走与起点相连的每一条边的概率都是\(\frac{1}{d_j}\)

然后对于整个图来说，第一步走每条边的概率就是第0步（1操作）选择这个点的概率*\(\frac{1}{d_j}\)，也就是\(\frac{d_j}{2m} * \frac{1}{d_j}=\frac{1}{2m}\)

于是\(f[1][j]=\sum\limits_{(u,j)∈e}\frac{1}{2m}=\frac{d_j}{2m}\)

同理：\(f[i][j]=\sum\limits_{(u,j)∈e}\frac{1}{2m}=\frac{d_j}{2m}\)

此时概率相同了。

\(E(x_1+x_2+……+x_n)=\sum\limits_{i=1}^nE(x_i)=\sum\limits_{i=1}^n\sum\limits_{j=1}^kx_i*f[j][i]*a_i\)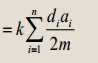

（依照定义还是比较好想的）其中xi表示是否在第i棵苹果树下0/1显然0的情况舍弃；

还有一步化简但是并不想写w

BZOJ4832 抵制克苏恩

你有一个英雄和若干奴隶主，对方每次攻击会从你的英雄和奴隶主中随机选一个造成一点伤害。奴隶主受到攻击后，体力为0则死亡，否则若场上奴隶主少于7个，则召唤一个3点血量的奴隶主。

有T局游戏，每局给出初始奴隶主的数量(<=7)和血量(<=3)，给出k，求对方攻击k次后你的英雄受到的总伤害值的期望。

T<=100， k<=50。

设\(f[i][a][b][c]\)表示还要进行i轮攻击，三种血量的奴隶主数量分别为a(血量为1)b(血量2)c(血量3)时，接下来英雄受到的期望总伤害。

设当前共有s=a+b+c个人，那么有1/s的概率打到英雄，a/s的概率打到血量为1的人，b/s的概率打到血量为2的人，c/s的概率打到血量为3的人。

咋的要这样设计状态倒着dp

打到英雄\(f[i-1][a][b][c]+=(f[i][a][b][c]+1)*\frac{1}{s+1};\)

打到a \(f[i-1][a-1][b][c/c+1]+=f[i][a][b][c]*\frac{a}{s+1};\) 此处c考虑奴隶主数是否<7

打到b \(f[i-1][a+1][b-1][c/c+1]+=f[i][a][b][c]*\frac{b}{s+1}\) 此处c考虑奴隶主数是否<7

打到c \(f[i-1][a][b+1][c-1/c]+=f[i][a][b][c]*\frac{c}{s+1}\) 此处c考虑奴隶主数是否<7

NOIP2016 换教室

小A的学校可以视为一个v个点的无向图，他有n门课程要按顺序上课，其中第i门课程要在节点ai进行，但还有一个备选地点bi。

现在小A有m个申请机会，若申请第i门课，那么将有ki的概率使课程搬到bi进行。每门课最多申请一次，而且要在全部申请完成后才知道是否成功，m次机会不必全部用完。他如何申请才能最小化在上课地点间移动的距离的期望值。求该期望值。

v<=300， n,m<=2000

f[i][j][0/1]表示前i个课程申请了j次，且第i个是否申请时的最小期望值。

$f[i][j][0]=Min(f[i-1][j][0]+dis(a[i-1],a[i]) ,

f[i-1][j][1]+k[i-1]dis(b[i-1],a[i])+(1-k[i-1])dis(a[i-1],a[i])) $

\(f[i][j][1]=Min(f[i-1][j-1][0]+dis(a[i-1],b[i])*k[i]+(1-k[i])*dis(a[i-1],a[i]),\\f[i-1][j-1][1]+dis(b[i-1],b[i])*k[i]*k[i-1]+dis(a[i-1]*b[i])*(1-k[i-1])*k[i]\\+dis(b[i-1],a[i])*k[i-1]*(1-k[i])+dis(a[i-1],a[i])*(1-k[i-1])*(1-k[i]));\)

时间复杂度O(v^3+nm)

BZOJ1076 奖励关

有n轮游戏和m种宝物，每种宝物有分数Pi（可以为负），每轮游戏会等概率抛出一种宝物，你可以选择吃或不吃。第i种宝物还有一个限制集合Si，表示只有在Si中的宝物都吃过后，才能吃第i种宝物。

求最优策略下的期望得分。

n<=100， m<=15

设\(f[i][S]\)为还剩下i轮游戏，吃过的宝物集合为S时，接下来能得到的最大期望得分。

==s=--i--

然后同样是倒着搞，最后答案就是当前一轮游戏都没进行，吃过的宝物为0的情况\(f[n][0]\)；初始状态是\(f[0][S]\)其中S是全集；

然后枚举第n-i轮游戏是不是吃了宝物；

如果没吃，显然第n-i轮和第n-i+1轮的结果相同，即\(f[i][S]=f[i-1][S]\)

如果吃了宝物，那么显然第n-i+1轮就多了一个宝物，又因为倒着转移，所以第n-i+1轮的结果要并上第n-i轮吃掉的宝物k，并且加上这个宝物的分数。即\(f[i][S]=f[i-1][S|(i<

合起来：\(f[i][S]=max\{f[i-1][S],f[i-1][S|(i<

网络题解：