JavaScript中求解最长回文子串的方法分析

在给定字符串s的情况下，任务是找到其中最长的回文子串。回文是指正读和反读都相同的字符串。解决这一问题的一个高效方法是使用Manacher算法。

Manacher算法的核心思想是在原始字符串的基础上构建一个新的字符串，通过在这个新字符串中插入特定的分隔符（如'#'），来简化回文检测的过程。例如，原始字符串S = 'abaaba'，经过转换后的新字符串T = '#a#b#a#a#b#a#'。这样做的目的是使任何长度的回文子串都能被视作以某个字符为中心向两侧扩展的形式，无论其原始长度是奇数还是偶数。

具体来说，对于每一个字符Ti，尝试以它为中心，向两边扩展，直到不能形成回文为止。这里的关键点在于计算出每个位置的最大回文半径。通过这种方式，可以有效地找到整个字符串中的最长回文子串。

在实现上，首先需要对原始字符串进行预处理，即在每个字符之间插入'#'，并在字符串的两端添加非字母字符（如'~'），以避免边界条件的特殊处理。接下来，遍历这个新的字符串，记录每个位置的回文半径，同时更新当前已知的最长回文子串的信息。最后，通过这些信息，可以轻松地从原始字符串中提取出最长的回文子串。

下面是一个简单的示例代码，展示了如何使用Manacher算法来解决问题：

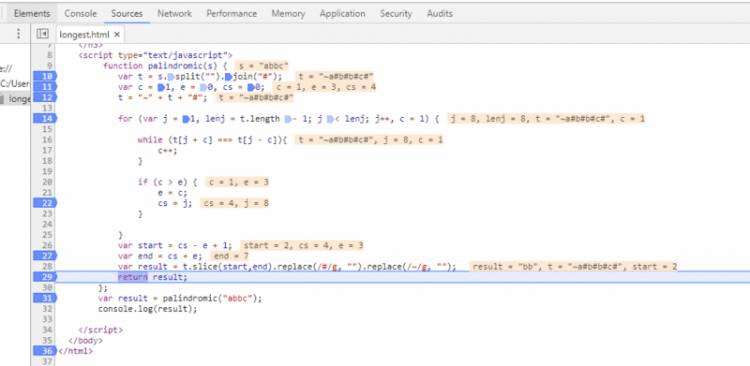
这段代码首先对输入字符串进行了预处理，包括在每个字符间插入'#'以及在字符串的两端添加'~'，以便于后续的回文检测。接着，通过遍历处理后的字符串，计算每个位置的最大回文半径，并根据这些信息确定最长回文子串的具体位置。最后，利用正则表达式去除多余的'#'和'~'，得到最终的结果。