二叉树的遍历问题

目录

一、二叉树

1、二叉树结点结构

2、递归遍历

3、非递归遍历

①非递归先序遍历

②非递归中序遍历

③非递归后序遍历

4、二叉树的宽度优先遍历

①宽度优先遍历

一、二叉树

1、二叉树结点结构

struct BinaryNode
{int val;BinaryNode* left;BinaryNode* right;
}

2、递归遍历

①先序遍历：对每一棵树和子树都是先遍历头结点，然后再是左结点，最后是右结点。

②中序遍历：对每一棵树和子树都是先遍历左结点，然后再是头结点，最后是右结点。

③后序遍历：对每一棵树和子树都是先遍历左结点，然后再是右结点，最后是头结点。

void recursion(struct BinaryNode * root)
{if (root == NULL){return;}//先序遍历printf("%d ", root->val);recursion(root->lChild);recursion(root->rChild);
}void recursion(struct BinaryNode * root)
{if (root == NULL){return;}recursion(root->lChild);//中序遍历printf("%d ", root->val);recursion(root->rChild);
}void recursion(struct BinaryNode * root)
{if (root == NULL){return;}recursion(root->lChild);recursion(root->rChild);//后序遍历printf("%d ", root->val);
}


 总结：第一次来到结点的时候打印就是先序遍历、第二次来到结点打印就是中序遍历、第三次来到结点打印就是后续遍历

3、非递归遍历

二叉树的非递归遍历需要用到栈容器，下面会对非递归遍历进行详细介绍

①非递归先序遍历

步骤：

(1) 先压入头节点

(2) 从栈中弹出一个结点cur

(3) 打印cur

(4) 先压右结点，再压左结点(如果有)

(5) 重复 (2) --- (4) 直到栈为空

代码如下:

//先序非递归
void prenorecursion(BinaryNode* headnode)
{printf("先序遍历:");if (headnode){stack s;s.push(headnode);while (s.size()){//1、弹出栈顶元素headnode = s.top();s.pop();//2、打印printf("%d ", headnode->m_Val);//3、如果有左右结点，先压入右结点，再压入左结点if (headnode->m_RightNode){s.push(headnode->m_RightNode);}if (headnode->m_LeftNode){s.push(headnode->m_LeftNode);}}}
}

②非递归中序遍历

中序非递归遍历的思想就是先把左边的结点全部压入到栈，直到为空，然后开始弹出结点并打印，弹出的时候将右边的结点也压入栈，重复上述步骤。

代码如下：

//中序非递归
void midnorecursion(BinaryNode* headnode)
{printf("中序遍历:");if (headnode){stack s;while (s.size() || headnode){//只要左结点不为空，一直压入栈中if (headnode){s.push(headnode);headnode = headnode->m_LeftNode;}//左边压完了，弹出结点的同时检查右边是否有结点，如果有，将右边结点压入并重复检测有无左结点else{headnode = s.top();printf("%d ", headnode->m_Val);s.pop();headnode = headnode->m_RightNode;}}}
}

③非递归后序遍历

步骤：

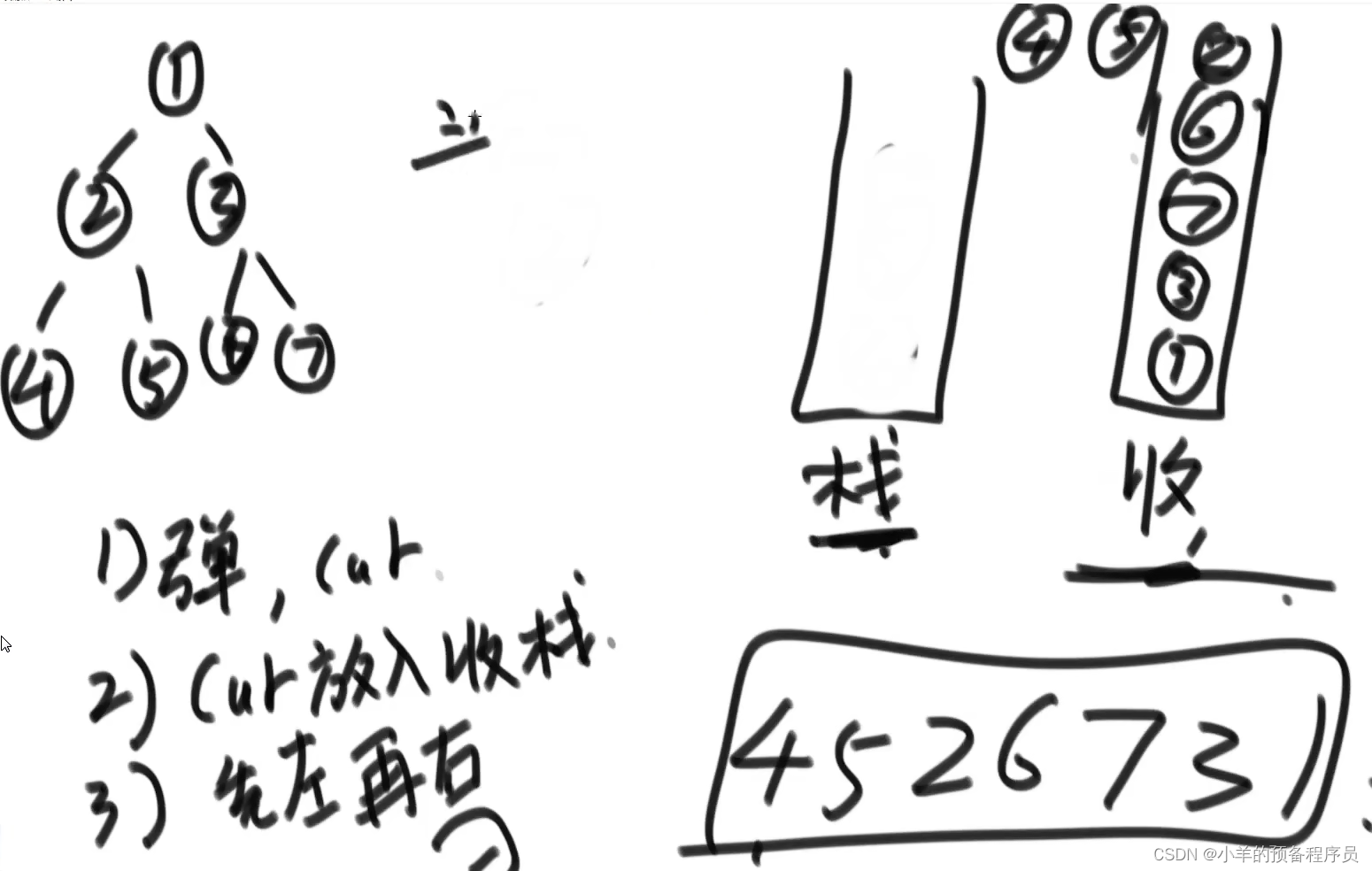
(1) 先压入头结点

(2) 弹出cur，将cur压入收集栈

(3) 先压左结点，再压右结点(如果有)

(4) 重复(2) --- (4) 直到栈为空

(5) 依次弹出收集栈元素并打印

 代码如下:

//后序非递归
void afternorecursion(BinaryNode* headnode)
{printf("后序遍历:");if (headnode){stack s;//容器栈stack collectstack;//收集栈//1、压入头结点s.push(headnode);while (s.size()){//2、弹出栈顶元素，并压入收集栈headnode = s.top();s.pop();collectstack.push(headnode);//3、将栈顶元素的左结点、右节点压入栈中(如果有的话)if (headnode->m_LeftNode){s.push(headnode->m_LeftNode);}if (headnode->m_RightNode){s.push(headnode->m_RightNode);}}//4、当栈中元素为空，依次弹出收集栈中元素并打印while (collectstack.size()){headnode = collectstack.top();printf("%d ", headnode->m_Val);collectstack.pop();}}
}

4、二叉树的宽度优先遍历

如何完成二叉树的宽度优先遍历（常见题目：求一颗二叉树的宽度）

①宽度优先遍历

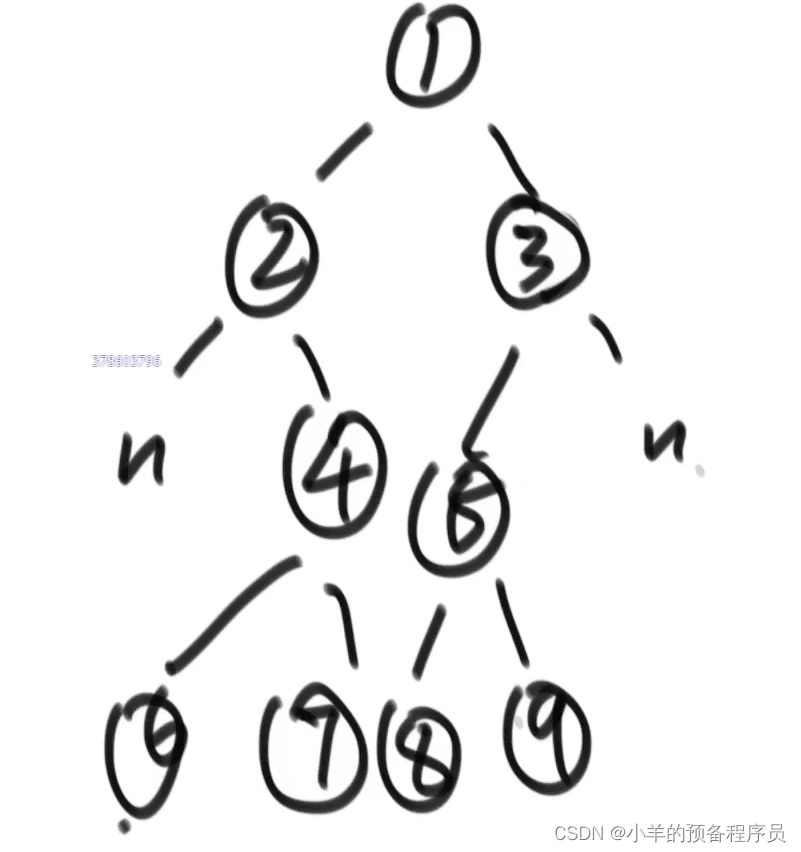
宽度优先遍历上图中就是 1->2->3->4->5->6->7->8->9

算法思想： 使用一个队列（可以是数组或链表）来完成。初始时只有一个根节点，然后每次取出一个结点，就把它的左右儿子（如果有）放入队列。

代码如下:

void treewidth(BinaryNode* headnode)
{queue q;//1、先放头节点q.push(headnode);while (q.size()){//2、弹出结点并打印headnode = q.front();printf("%d ", headnode->m_Val);q.pop();//3、放入左结点和右节点(如果有)if (headnode->m_LeftNode){q.push(headnode->m_LeftNode);}if (headnode->m_RightNode){q.push(headnode->m_RightNode);}}
}