纠删码（ErasureCode）技术详解

纠删码技术概述

1. 什么是纠删码？

纠删码（Erasure Code, EC）是一种用于提高数据可靠性的编码技术。它通过增加冗余校验信息，使数据在部分丢失或损坏时仍能被恢复。具体来说，EC将数据分成多个分片，并生成一定数量的校验分片。假设将数据分成k个分片，生成m个校验分片，总共有n=k+m个分片。在这种情况下，只要能够获取到任意k个分片，就能恢复原始数据。

纠删码不仅广泛应用于数据存储领域，还在通信领域发挥着重要作用。

2. EC(4+2)编解码简介

下图展示了EC(4+2)的编解码及故障恢复过程：

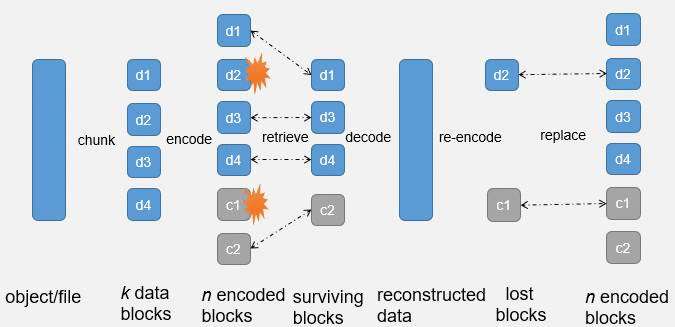
• 分片（Chunk）：将数据分成4个分片，分别为d1、d2、d3、d4。
• 编码（Encode）：根据4个数据分片生成2个校验分片，形成4+2的EC数据结构。
• 故障：允许6个分片中任意2个分片损坏，例如d2和c1。
• 解码（Decode）：通过剩余的4个分片（d1、d3、d4、c2），利用EC算法恢复原始数据。
• 重编码（Re-encode）：将恢复后的数据重新分片，并计算新的校验分片。
• 替换（Replace）：用新计算的分片替换损坏的分片（d2、c1）。

与传统的副本技术相比，EC的故障恢复过程更为复杂，但其优势在于存储成本更低。例如，与3副本相比，EC可以在保证相同可靠性的情况下，减少存储空间的需求。

3. 纠删码的数学原理

下图展示了EC的数学原理：

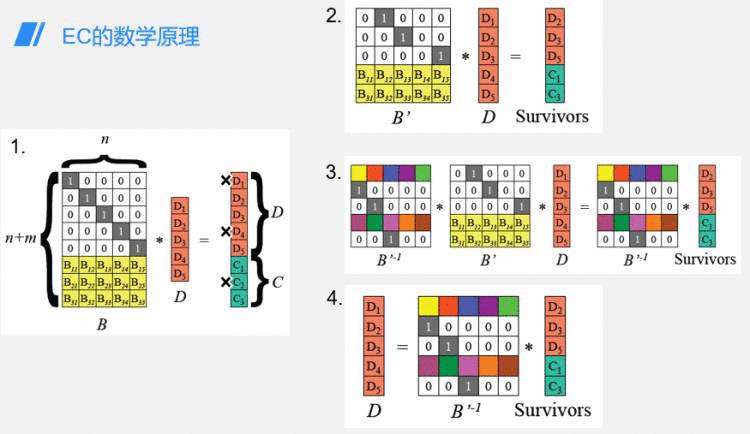
• B矩阵：B是一个(5+3)行5列的矩阵，其特点是任意5阶方阵都是可逆矩阵。
• 数据分片（D）：数据被分成5个分片，分别为D1、D2、D3、D4、D5。

根据矩阵乘法，B * D 的结果是一个(5+3)行1列的矩阵，即D1、D2、D3、D4、D5、C1、C2、C3。这种(5+3)的EC策略允许任意3个分片丢失。

假设D1、D4、C2损坏，仍然存在等式 B' * D = D2、D3、D5、C1、C3。由于B'存在可逆矩阵，两边同时乘以B'的逆矩阵，可以得到原始数据D：D1、D2、D3、D4、D5。最后，通过B * D计算出损坏的D1、D4、C2，从而实现故障恢复。

符合B矩阵要求的矩阵类型包括：

• 范德蒙矩阵（Vandermonde Matrix）：在高等数学中常见。
• 柯西矩阵（Cauchy Matrix）：同样在数学中有广泛应用。
• 其他满足条件的矩阵。

4. EC存储的优缺点

优点：

• 磁盘利用率高，存储成本低，通常仅为3副本存储的一半甚至更低。
• 在写操作时，网络开销较低，尤其是与3副本相比。

缺点：

• 在编解码过程中，CPU占用和网络开销较大，尤其是在写操作和故障恢复时。
• EC必须进行满条带读写，不足条带时需要填充（Padding）。
• 与3副本相比，EC存储系统更为复杂，对集群稳定性提出了更高要求。

由于上述缺点，EC最初并未广泛应用于在线数据存储，而更多地用于低频存储场景，即访问频率较低的数据存储系统。然而，随着技术的发展，越来越多的在线存储系统也开始采用EC编码。